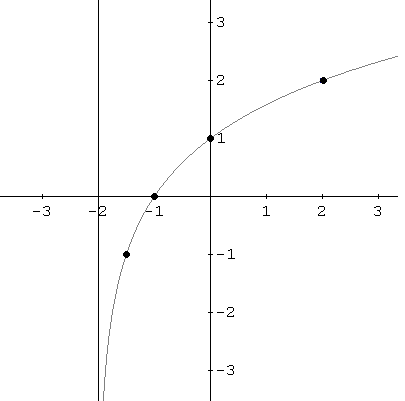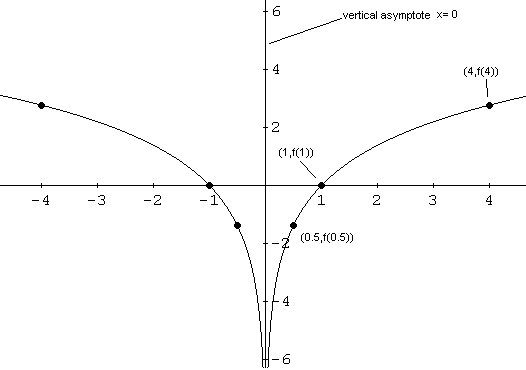| |
| Revisione Per prima cosa si aprono con le propriet� del grafico della funzione logaritmica di base di base di uno, f (x) = log a (x), a> 0 e non uguale a 1. Il dominio della funzione f � l'intervallo (0, + inf). La gamma di f � l'intervallo (-inf, + inf). L'inf simbolo significa infinito. Funzione f ha un asintoto verticale data da x = 0. Questa funzione ha una intercetta x in (1, 0). f aumenta man mano che aumenta x. Esempio 1: f � una funzione data da f (x) = log2 (x + 2)
Risposta a Esempio 1 a - Il dominio di f � l'insieme di tutti i valori x tali che� x + 2> 0 x > -2 La gamma di f � l'intervallo (-inf, + inf). b - l'asintoto verticale si ottiene risolvendo �x + 2 = 0 che d� �x = -2 Per x che tende -2 da destra (x > -2), f (x) diminuisce senza limiti. Come facciamo a saperlo? Prendiamo alcuni valori: f (-1) = log 2 (-1 + 2) = log 2 (1) = 0 f (-1,5) = log 2 (-1,5 + 2) = log 2 (1 / 2) = -1 f (-1,99) = log 2 (-1,99 + 2) = log 2 (0,01), che � approssimativamente uguale a -6,64 f (-1,999999) = log 2 (-1,999999 + 2) = log 2 (0,000001), che � approssimativamente uguale a -19,93. c - Per trovare l'intercetta x abbiamo bisogno di risolvere l'equazione f (x) = 0 log2 (x - 2) = 0 Utilizzare le propriet� delle funzioni esponenziali e logaritmiche a scrivere l'equazione di cui sopra, come (x - 2) = 20 Poi semplificare �x + 2 = 1 x = -1 L'intercetta x � in (-1, 0). L'intercetta y � data da (0, f (0)) = (0, log 2 (0 + 2)) = (0, 1). d - Finora abbiamo il dominio, gamma, X e Y e intercetta l'asintoto verticale. Abbiamo bisogno di pi� punti. Consideriamo un punto x = -3 / 2 (a met� strada tra l'intercetta x e l'asintoto verticale) e un altro punto in x = 2. f (-3 / 2) = log 2 (-3 / 2 + 2) = log 2 (1 / 2) = log 2 (2 -1) = -1. f (2) = log 2 (2 + 2) = log 2 (22) = 2. Ora abbiamo pi� informazioni su come grafico f. Il grafico aumenta con l'aumentare x. Vicino alla asintoto verticale x = -2, il grafico di f diminuisce senza limite per x che tende -2 dalla destra. Il grafico non tagli l'asintoto verticale. Ora unire i vari punti da una curva regolare.
Problema abbinate a Esempio 1: f � una funzione data da f (x) = log2(x+3) �
Esempio 2: f � una funzione data da f (x) = -3 ln(x - 4) �
Risposta a Esempio 2 a - Il dominio di f � l'insieme di tutti i valori x tali che� x - 4 > 0 oppure x > 4 La gamma di f � l'intervallo (-inf, + inf). b - l'asintoto verticale si ottiene risolvendo �x - 4 = 0 x = 4 Come si avvicina x 4 da destra (x> 4), f (x) aumenta senza limite. Come facciamo a saperlo? Prendiamo alcuni valori: f (5) = ln (5-4) = -3ln (1) = 0 F (4,001) =- 3ln (0.001), che � pari a circa 20,72. f (4.000001) = -3ln (0,000001), che � pari a circa 41,45. c - Per trovare l'intercetta x abbiamo bisogno di risolvere l'equazione f (x) = 0 -3ln(x - 4) = 0 Dividere entrambi i lati da -3 a ottenere ln (x - 4) = 0 Utilizzare le propriet� delle funzioni esponenziali e logaritmiche a scrivere l'equazione di cui sopra, come e ln (x - 4) = e 0 Poi semplificare �x - 4 = 1 x = 5 L'intercetta x � (5, 0). L'intercetta y � data da (0, f (0)). f (0) � indefinito poich� x = 0 non � un valore nel dominio di f. Non vi � alcun intercetta su y. d - Finora abbiamo il dominio, gamma, x intercettare e l'asintoto verticale. Abbiamo bisogno di punti extra per poter grafico di f. f (4,5) = -3ln (4,5 - 4) pari a circa 2,08 f (8) = -3ln (8 - 4) pari a circa - 4.16 f (14) = -3ln (14 - 4) pari a circa - 6,91 Vediamo ora sketch tutti i punti e l'asintoto verticale. Congiungono i punti da una curva regolare e f aumenta man mano che si avvicina x 4 da destra.
� Problema abbinate a Esempio 2: f � una funzione data da f (x) = 2ln(x + 5) �
Esempio 3: f � una funzione data da f (x) = 2ln (| x |) �
Risposta a Esempio 3 a - Il dominio di f � l'insieme di tutti i valori x tali che x > 0 Il dominio � l'insieme di tutti i numeri reali tranne 0. La gamma di f � l'intervallo (-inf, + inf). b - l'asintoto verticale si ottiene risolvendo |x| = 0 che d� x = 0 Come x si avvicina a 0 da destra (x > 0), f (x) diminuisce senza limiti. Come facciamo a saperlo? Prendiamo alcuni valori: f (1) = 2 ln (| 1 |) = 0 f (0.1) = 2ln (0,1), che � approssimativamente uguale a -4,61. f (0,0001) = 2ln (0,0001) che � pari a circa -18,42. f (0.0000001) = 2ln (0,0000001) che � pari a circa -32,24. Come x si avvicina a 0 da sinistra (x <0), f (x) diminuisce senza limiti. Come facciamo a saperlo? Prendiamo alcuni valori: f (-1) = 2 ln (| -1 |) = 0 f (-0,1) = 2ln (| -0,1 |), che � approssimativamente uguale a -4,61. f (-0,0001) = 2ln (| -0,0001 |), che � approssimativamente uguale a -18,42. f (-0,0000001) = 2ln (| -0,0000001 |), che � approssimativamente uguale a -32,24. c - Per trovare l'intercetta x abbiamo bisogno di risolvere l'equazione f (x) = 0 2ln (| x |) = 0 Dividere entrambi i lati da 2 per ottenere ln (| x |) = 0 Utilizzare le propriet� delle funzioni esponenziali e logaritmiche a scrivere l'equazione di cui sopra, come e ln (| x |) = e 0 Poi semplificare �| X | = 1 Due x intercetta a (1, 0) e (-1, 0). L'intercetta y � data da (0, f (0)). f (0) � indefinito poich� x = 0 non � un valore nel dominio di f. Non vi � alcun intercetta su y. d - Finora abbiamo il dominio, gamma, x intercettare e l'asintoto verticale. Con lo studio della funzione f � facile dimostrare che questa � una funzione pari e il suo grafico � simmetrico rispetto all'asse y. f (x) = 2 ln (|-x |) ma |-X | = | x | e quindi f (x) = 2 ln (| x |) = f (x), ci� dimostra che f � una funzione pari. Cerchiamo punti extra. f (4) = 2LN (| 4 |) pari a circa 2,77. f (0.5) = 2LN (| 0,5 |) pari a circa - 1.39. Poich� f � anche f (-4) = f (4) e f (-0,5) = f (0,5). Vediamo ora sketch tutti i punti, l'asintoto verticale e unirsi ai punti da una curva regolare.
Problema abbinate a Esempio 3: f � una funzione data da f (x) = -2ln (x 2)
Riferimenti pi� sulle funzioni logaritmiche e grafica. |