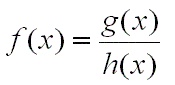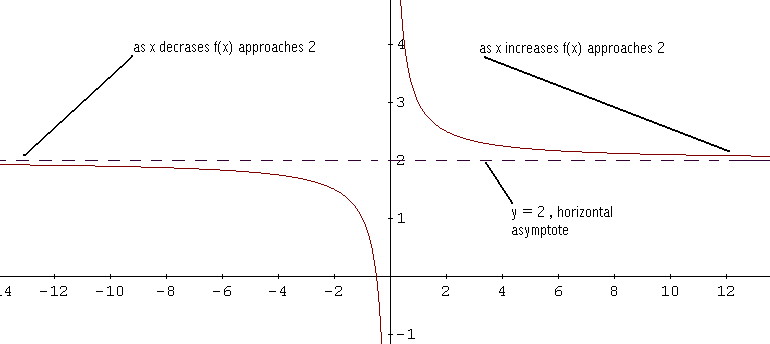| |
| Definizione Una funzione razionale f ha la forma
dove g (x) e h (x) sono funzioni polinomiali. Il dominio di f � l'insieme di tutti i numeri reali, tranne i valori di x che rendono il denominatore h (x) pari a zero. In ci� che segue, si assume che g (x) e h (x) non hanno elementi in comune. Asintoti verticali Lasciare
Il dominio di f � l'insieme di tutti i numeri reali tranne 3, dal 3 rende il denominatore zero e la divisione per zero non � consentita in matematica. Tuttavia possiamo cercare di scoprire come si fa il grafico di f si comportano vicino a 3. Cerchiamo di valutare la funzione f a valori di quasi 3 x tale che x <3. I valori sono riportati nella tabella sottostante:
Ora a valutare f a valori di quasi 3 x tale che x> 3.
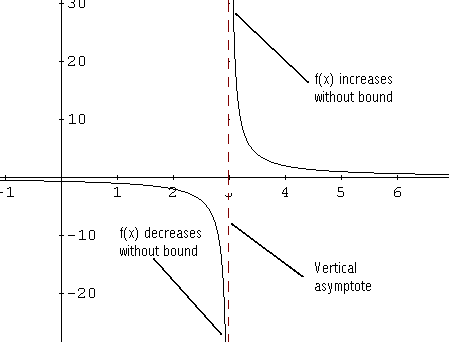
Il grafico di f � mostrato sotto.
Note 1 - Come si avvicina x 3 da sinistra o da valori inferiori a 3, f (x) diminuisce senza limiti. 2 - Come si avvicina x 3 da destra o da valori superiori a 3, f (x) aumenta senza limite. Diciamo che la linea x = 3, linea spezzata, � l'asintoto verticale per il grafico di f. In generale, la linea x = a � un asintoto verticale per il grafico di f se f (x) aumenta o diminuisce senza limite come x si avvicina ad una da destra o da sinistra. Questo � simbolicamente scritto come:
Asintoti orizzontali Lasciare
1 - Sia x crescere e trovare i valori di f (x).
2 - Sia x diminuire e trovare i valori di f (x).
Come | x | aumenta, il numeratore � dominato dal termine 2x e il numeratore ha un solo termine x. Quindi f (x) assume valori vicini a 2x / x = 2. Vedere il comportamento grafico qui sotto.
In generale, la retta y = b � un asintoto orizzontale per il grafico di f se f (x) si avvicina a un b costante x aumenti o diminuzioni senza limiti. Come trovare l'asintoto orizzontale? Sia F una funzione razionale definita come segue
Teorema m � il grado del polinomio al numeratore e n � il grado del polinomio al numeratore. Caso 1: Per m <n, l'asintoto orizzontale � la retta y = 0. Caso 2: Per m = n, l'asintoto orizzontale � la retta y = a m / b n Caso 3: Per m> n, non c'� asintoto orizzontale. Esempio 1: Sia f una funzione razionale definita dalla
a - Trovare il dominio di f. b - Trova la x e intercetta y del grafico di f. c - Trova la asintoti verticali e orizzontali per il grafico di f se ce ne sono. d - Utilizzare le tue risposte alle parti a, b, c sopra per tracciare il grafico della funzione f. Risposta a Esempio 1 a - Il dominio di f � l'insieme di tutti i numeri reali tranne x = 1, dal momento che questo valore di x rende il denominatore zero. b - L'intercetta x si trova risolvendo f (x) = 0 o x +1 = 0. L'intercetta x � il punto (-1, 0). L'intercetta y � il punto (0, f (0)) = (0, -1). c - l'asintoto verticale � data dalla zero del denominatore x = 1. Il grado del numeratore � 1 e il grado del denominatore � 1. Sono uguali e secondo il teorema di cui sopra, l'asintoto orizzontale � la retta y = 1 / 1 = 1 E - Anche se le parti a, b, c dare alcune informazioni importanti circa il grafico di f, abbiamo ancora bisogno di costruire una tabella di firmare per la funzione f in modo da essere in grado di tracciare con facilit�. Il segno di f (x) cambiamenti a gli zeri del numeratore e denominatore. Per trovare la tabella di segno, si procede come nel risolvere le disuguaglianze razionali. Gli zeri del numeratore e denominatore che sono -1 e 1 divide la linea numero reale in intervalli di 3: (- Infinito, -1), (-1, 1), (1, + infinito). Scegliamo un valore di prova all'interno di ogni intervallo e trovare il segno di f (x). A (- infinito, -1), -2 selezionare e trovare f (-2) = (-2 + 1) / (-2 - 1) = 1 / 3> 0. In (-1, 1), 0 selezionare e trovare f (0) = -1 <0. In (1, + infinito), 2 selezionare e trovare f (2) = (2 + 1) / (2 - 1) = 3> 0. Diciamo pure che tutte le informazioni su F in una tabella.
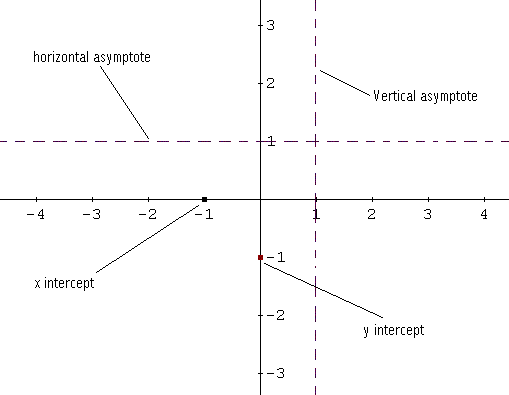
Nella tabella di cui sopra AV significa asintoto verticale. Per tracciare il grafico di f, iniziamo disegnando il x e y intercetta e gli asintoti verticali e orizzontali in linee spezzate. Vedi schema qui sotto.
Ora inizia ad abbozzare il grafico di f a partire da sinistra. Nell'intervallo (-inf, -1) f (x) � positivo quindi il grafico � sopra l'asse x. A partire da sinistra, abbiamo schizzo f tenendo conto del fatto che y = 1 � un asintoto orizzontale: il grafico di f � vicino a questa linea a sinistra. Vedi schema qui sotto.
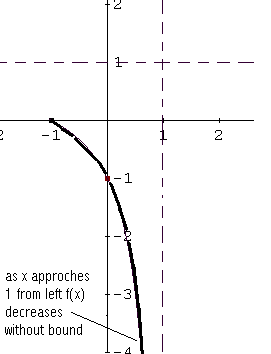
Tra -1 e 1 f (x) � negativo, quindi il grafico di f � sotto l'asse x. (0, -1 intercetta) � ay e x = 1 � un asintoto verticale: come x tende a 1 da sinistra f (x) Defunti senza limiti, perch� f (x) <0 in (-1, 1). Vedi schema qui sotto.
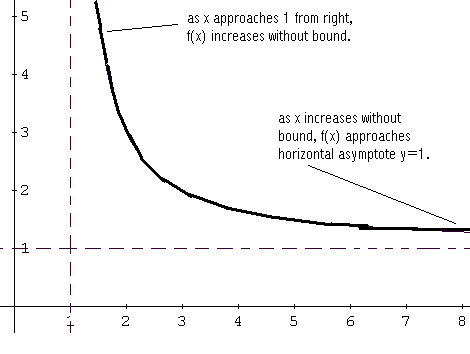
Per x> 1, f (x)> 0 quindi il grafico � sopra l'asse x. Come x tende a 1 da destra, il grafico di f aumenta senza limite (f (x)> 0). Anche al crescere x, il grafico di f approcci y = 1 l'asintoto orizzontale. Vedi schema qui sotto.
Ora mettere tutti i pezzi "del grafico di f insieme per ottenere il grafico di f.
Abbinate Problema: Sia f una funzione razionale definita dalla f (x) = (-x + 2) / (x + 4) a - Trovare il dominio di f. b - Trova la x e intercetta y del grafico di f. c - Trova la asintoti verticali e orizzontali per il grafico di f se ce ne sono. d - Utilizzare le tue risposte alle parti A, b, c sopra per tracciare il grafico della funzione f. Riferimenti pi� sulla grafica e le funzioni razionali. |