Quoziente di differenza (Difference quotient)
Qual è il quoziente di differenza nel calcolo infinitesimale?
Iniziamo con la definizione e poi calcoliamo il quoziente di differenza per diverse funzioni come esempi con spiegazioni dettagliate.
Tieni presente che è incluso un calcolatore del quoziente di differenza che può essere utilizzato per verificare i risultati e generare ulteriori pratica.
\( \)\( \)\( \)\( \)
Definizione di quoziente di differenza (Definition of Difference Quotient)
Sia \( f \) una funzione il cui grafico è mostrato di seguito.
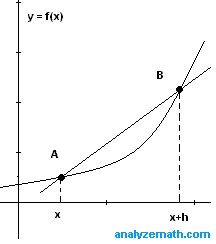
A e B sono punti sul grafico di \( f\). Una linea che passa per i due punti \( A ( x , f(x)) \) e \( B (x+h , f(x+h)) \) è chiamata retta secante. La pendenza \( m \) della linea secante può essere calcolata come segue:
\[
m = \dfrac{f (x + h) - f(x)}{(x + h) - x}
\]
Semplificare il denominatore da ottenere
\[
m = \dfrac{f (x + h) - f(x)}{h}
\]
La pendenza \( m \) è chiamata quoziente di differenza. È un concetto molto importante nel calcolo infinitesimale dove viene utilizzato per definire la derivata di una funzione \( f \) che di fatto definisce la variazione locale di una funzione in matematica.
Esempi con soluzioni
Negli esempi seguenti, calcoliamo e semplifichiamo i quozienti di differenza di diverse funzioni.
Esempio 1
Trova la differenza quoziente della funzione \( f \) definita da
\[f(x) = 2x + 5\]
Soluzione dell'Esempio 1
- Dobbiamo prima calcolare \( f(x + h) \).
\(
f(x + h) = 2(x + h) + 5
\)
- Sostituiamo ora \( f(x + h) \) e \( f(x) \) nella definizione del quoziente differenziale con le loro espressioni
\(
\dfrac{f (x + h) - f(x)}{h} = \dfrac{2(x + h) + 5 - (2 x + 5) }{h}
\)
- Semplifichiamo l'espressione precedente.
\(
= \dfrac{2h}{2} = 2
\)
- La risposta è 2 quale è anche la pendenza della retta definita dalla funzione \( f \), perché?
Esempio 2
Trova la differenza quoziente della seguente funzione
\[ f(x) = 2x^2 + x - 2 \]
Soluzione dell'Esempio 2
- Per prima cosa calcoliamo \( f(x + h) \).
\(
f(x + h) = 2(x + h)^2 + (x + h) - 2
\)
- Ora sostituiamo \( f(x + h) \) e \( f(x) \) nel quoziente differenza
\(
\dfrac{f (x + h) - f(x)}{h}
= \dfrac{ 2(x + h)^2 + (x + h) - 2 - ( 2 x^2 + x - 2 )}{h}
\)
- Espandiamo le espressioni al numeratore e raggruppiamo termini simili.
\(
= \dfrac{ 4 x h + 2 h^2 + h}{h} = 4 x + 2 h +1
\)
Esempio 3
Trova la differenza quoziente della funzione \( f \) data da
\[ f(x) = \peccato x \]
e scrivi il risultato come prodotto.
Soluzione dell'esempio 3
- Per prima cosa calcoliamo \( f(x + h) \).
\(
f(x + h) = \sin (x + h)
\)
- Sostituiamo ora \( f(x + h) \) e \( f(x) \) nel quoziente differenza
\(
\dfrac{f (x + h) - f(x)}{h}
= \dfrac{ \sin (x + h) - \sin x}{h}
\)
- Utilizziamo la formula trigonometrica che trasforma una differenza \( \ quad \sin (x + h) - \sin x \quad \) in un prodotto.
\(
\sin (x + h) - \sin x = 2 \cos [ (2 x + h)/2 ] \sin (h/2)
\)
- Sostituiamo l'espressione sopra con \( sin (x + h) - sin x \) nel quoziente di differenza sopra da ottenere.
\(
\dfrac{f (x + h) - f(x)}{h}
= \dfrac{ 2 \cos [ (2 x + h)/2 ] \sin (h/2)}{h}
\)
Altri riferimenti e collegamenti
Calcolatore del quoziente di differenza
differenziazione e derivate
Quoziente di differenza

