Il teorema di Bayes per trovare le probabilità condizionali viene spiegato e utilizzato per risolvere esempi che includono spiegazioni dettagliate. I diagrammi sono usati per dare una spiegazione visiva al teorema. Vengono discussi anche i risultati numerici ottenuti per comprendere le possibili applicazioni del teorema.

Teorema di Bayes

Uso degli esempi di teom di Bayes con soluzioni dettagliate

L'esempio 1 di seguito è progettato per spiegare l'uso del teorema di Bayes e anche per interpretare i risultati forniti dal teorema.
Esempio 1
Una delle due scatole contiene 4 palline rosse e 2 palline verdi e la seconda scatola contiene 4 palline verdi e due rosse. In base alla progettazione, le probabilità di selezionare a caso la casella 1 o la casella 2 sono 1/3 per la casella 1 e 2/3 per la casella 2.
Una casella viene selezionata a caso e una pallina viene estratta a caso da essa.
a) Dato che la pallina estratta è rossa, qual è la probabilità che sia stata estratta dalla prima casella?
b) Dato che la pallina estratta è rossa, qual è la probabilità che sia stata estratta dalla seconda casella?
c) Confrontare i risultati delle parti a) eb) e spiegare la risposta.

Soluzione dell'esempio 1
Chiamiamo la prima casella B1 e la seconda casella B2
Lascia che l'evento E1 sia "seleziona casella 1" e l'evento E2 "seleziona casella 2".
Sia l'evento R "seleziona una pallina rossa".
Tutte le informazioni di cui sopra sono incluse nel diagramma sottostante.


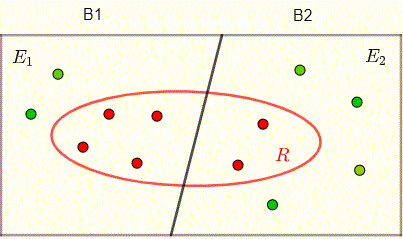
Le probabilità di selezionare una delle due caselle sarebbero date (sopra) da
\(P(E_1) = 1/3\) e \(P(E_2) = 2/3\)
La probabilità condizionata che una pallina selezionata sia rossa dato che è selezionata dalla casella 1 è data da
\( P(R | E_1) = 4/6 = 2/3\) , 4 palline su 6 sono rosse nella casella 1
La probabilità condizionata che una pallina selezionata sia rossa dato che è selezionata dalla casella 2 è data da
\( P(R | E_2) = 2/6 = 1/3\) , 2 palline su 6 sono rosse nella casella 2
a)
La questione è trovare la probabilità condizionata che la pallina sia estratta dalla casella 1 dato che è rossa, è data dal teorema di Bayes.
\( P(E_1|R) = \dfrac{P(R | E1) P(E1) }{ P(R | E1) P(E1) + P(R | E2) P(E2) } \)

\( = \dfrac{ 2/3 * 1/3}{2/3 * 1/3 + 1/3 * 2/3} = 1/2 \)
b)
La questione è trovare la probabilità condizionata che la pallina sia estratta dalla casella 2 dato che è rossa, è data dal teorema di Bayes.
\( P(E_2|R) = \dfrac{P(R | E2) P(E2) }{ P(R | E1) P(E1) + P(R | E2) P(E2) } \)

\( = \dfrac{ 1/3 * 2/3}{2/3 * 1/3 + 1/3 * 2/3} = 1/2 \)
c)
Le due probabilità calcolate nelle parti a) eb) sono uguali.
Sebbene ci siano più palline rosse nella casella 1 che nella casella 2 (il doppio), le probabilità calcolate sopra sono uguali perché la probabilità di selezionare la casella 2 è maggiore (il doppio) della probabilità di selezionare la casella 1. Teorema di Bayes prende in considerazione tutte le informazioni.

Esempio 2
L'1% di una popolazione ha una certa malattia e il restante 99% è esente da questa malattia. Viene utilizzato un test per rilevare questa malattia. Questo test è positivo nel 95% delle persone con la malattia ed è anche (falsamente) positivo nel 2% delle persone libere dalla malattia.
Se una persona, scelta a caso da questa popolazione, è risultata positiva, qual è la probabilità che abbia la malattia?

Soluzione dell'esempio 2
Sia D l'evento "avere la malattia" e FD l'evento "libero dalla malattia"
Sia l'evento TP l'evento in cui il "test è positivo".
Di seguito è riportato un diagramma con tutte le informazioni di cui sopra.


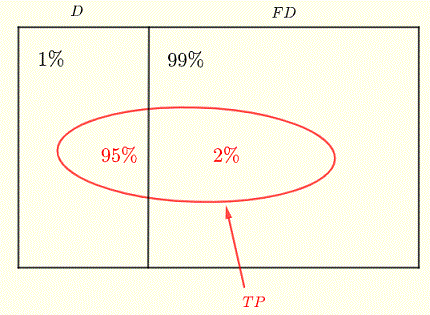
La probabilità che una persona abbia la malattia dato che è risultata positiva è data dal teorema di Bayes:
\( P(D | TP) = \dfrac{P(TP | D) P(D) }{ P(TP | D) P(D) + P(TP | ND) P(ND) } \)

\( \quad \quad \quad = \dfrac{95\% 1\%}{95\% 1\% + 2\% 99\% } = 0,32\)

Sebbene una persona risulti positiva, la probabilità di avere la malattia è piuttosto bassa.
Spiegazione
Si noti che anche quando una persona risulta positiva ciò non significa che abbia la malattia; e questo perché il numero di liberi da malattia (99%) è molto più alto di quelli che ce l'hanno la malattia (1%).
Cerchiamo di chiarire i risultati ottenuti sopra utilizzando alcuni numeri concreti.
Supponiamo che vengano testate 1000 persone
liberi da malattia sono: \( 99\% \times 1000 = 990\) e    \( 2\% \times 990 = 19,8 \approx 20\) test positivo
Persone con malattia: \( 1\% \times 1000 = 10\) e    \( 95\% \times 10 = 9,5 = 9,5 \approx 10\) test positivo
Di tutti coloro che sono risultati positivi che sono    20 + 10 = 30    solo 10 hanno la malattia.
La percentuale di coloro che risultano positivi ma non hanno la malattia è data da: 9,5 / (19,8 + 9,5) = 0,32
che è la probabilità \( P(D | TP) \) calcolata sopra.

Esempio 3
Tre fabbriche producono lampadine per rifornire il mercato. La fabbrica A produce il 20%, il 50% degli utensili viene prodotto nelle fabbriche B e il 30% nella fabbrica C.
Il 2% delle lampadine prodotte nello stabilimento A, l'1% delle lampadine prodotte nello stabilimento B e il 3% delle lampadine prodotte nello stabilimento C sono difettose.
Una lampadina viene scelta a caso sul mercato e trovata difettosa. qual è la probabilità che questa lampadina sia stata prodotta dalla fabbrica B?

Soluzione dell'esempio 3
Siano \( P(A) = 20\% \), \( P(B) = 50\% \) e \( P(C) = 30\% \) rappresentino le probabilità che una lampadina selezionata a caso provenga da fabbrica A, B e C rispettivamente.
Sia \( P(D) \) la probabilità che venga selezionata una lampadina difettosa.
Siano \( P(D | A) = 2\% \), \( P(D | B) = 1\% \) e \( P(D | C) = 3\%\) rappresentino la probabilità condizionate che una lampadina sia difettosa dato che è stata selezionata rispettivamente dalla fabbrica A, B e C.
Calcoliamo ora la probabilità condizionata che la lampadina sia stata prodotta dalla fabbrica B dato che è difettosa scritta come \( P(B | D) \) e data dal teorema di Bayes.

\( P(B | D) = \dfrac{P(D | B) P(B) }{ P(D | A) P(A) + P(D | B) P(B) + P(D | C) P(C)}\)

\( = \dfrac{1\% \times 50\%}{ 2\% \times 20\% + 1\% \times 50\% + 3\% \times 30\%} = 0,2777\)

Sebbene la fabbrica B produca il 50% delle lampadine, la probabilità che la lampadina selezionata (difettosa) provenga da questa fabbrica è bassa perché le lampadine prodotte da questa fabbrica hanno una bassa probabilità (1%) di essere difettose.

Esempio 4
Un sistema radar è progettato in modo tale che la probabilità di rilevare la presenza di un aereo nel suo raggio sia del 98%. Tuttavia, se nessun aereo è presente nel suo raggio, segnala comunque (falsamente) che un aereo è presente con una probabilità del 5%. In qualsiasi momento, la probabilità che un aeromobile sia presente nel raggio del radar è del 7%.
a) Qual è la probabilità che nessun aereo sia presente nel raggio del radar dato che viene rilevato un aereo?
b) Qual è la probabilità che un aereo sia presente nel raggio del radar dato che un aereo viene rilevato?
c) Qual è la probabilità che un aereo sia presente nel raggio del radar dato che non viene rilevato alcun aereo?
d) Qual è la probabilità che nessun aereo sia presente nel raggio del radar dato che non viene rilevato alcun aereo?

Soluzione dell'esempio 4
Useremo le notazioni del complemento.
Sia \( A \) l'evento in cui è presente un aeromobile e \( A^c \) il complemento di eventi di \( A \) che significa che non è presente alcun aeromobile.
La probabilità che si verifichi A è data come
\( P(A) = 7\% \)
E
\( P(A^c) = 100\% - 7\% = 93\% \)
Sia \( D \) l'evento in cui un aereo viene rilevato dal sistema radar e \( D^c \) il complemento di \( D \) che significa che non viene rilevato alcun aereo.
La probabilità condizionata che un aeromobile venga rilevato dato che è presente è data sopra ed è scritta come
\( P(D | A) = 98%\)
\( P(D | A^c) = 5% \)
a)
Metti tutte le informazioni di cui sopra in un diagramma di Venn come mostrato di seguito.


Usa il teorema di Bayes per scrivere la probabilità che nessun aereo sia presente nel raggio del radar dato che viene rilevato un aereo

\( P(A^c | D) = \dfrac{ P(D | A^c) P(A^c) }{ P(D | A^c) P(A^c) + P(D | A ) PAPÀ)} \)

\( = \dfrac{5\% \times 93\%}{5\% \times 93\% + 98\% \times 7\%} \approx 0,4040\)

b)
Usa il teorema di Bayes per scrivere la probabilità che un aereo sia presente nel raggio del radar dato che un aereo viene rilevato
\( P(A | D) = \dfrac{ P(D | A) P(A) }{ P(D | A) P(A) + P(D | A^c) P(A^c)} \)

\( = \dfrac{98\% \times 7\%}{98\% \times 7\% + 5\% \times 93\%} \approx 0,5960 \)

c)
Per prima cosa dobbiamo calcolare le seguenti probabilità
\( P(D^c | A) = 100\% - 98\% = 2\% \)
\( P(D^c | A^c) = 100\% - 5\% = 95\% \)
Metti tutte le informazioni di cui sopra in un diagramma di Venn come mostrato di seguito.



Usa il teorema di Bayes per scrivere la probabilità che un aereo sia presente nel raggio del radar dato che non viene rilevato alcun aereo

\( P(LA | RE^c) = \dfrac{ P(RE^c | LA) P(LA) }{ P(RE^c | LA) P(LA) + P(RE^c | LA^c ) P(A^c)} \)

\( = \dfrac{2\% \times 7\%}{2\% \times 7\% + 95\% \times 93\%} \approx 0.0016\)

d)
Usa il teorema di Bayes per scrivere la probabilità che nessun aereo sia presente nel raggio del radar dato che nessun aereo viene rilevato

\( P(LA^c | RE^c) = \dfrac{ P(RE^c | LA^c) P(LA^c) }{ P(RE^c | LA^c) P(LA^c) + P(D^c | A) P(A)} \)

\( = \dfrac{95\% \times 93\%}{95\% \times 93\% + 2\% \times 7\%} \approx 0,9984 \)

NOTA Tutti i calcoli di cui sopra possono essere eseguiti con l'aiuto di un diagramma ad albero mostrato di seguito. Una volta che il diagramma ad albero ha tutte le probabilità, è più facile usare queste probabilità nel teorema di Bayes per valutare i risultati finali.

Altri riferimenti e collegamenti