Solve Least Squares Problems by the QR Decomposition
Least Square Problem
In many real life problem solving, when a solution \( x \) to a system of equations of the form
\[ A x = B \]
cannot be found (i.e. the system is inconsistent), an approximate solution 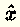\( \hat x \) to the given system \( A x = B \) may be enough.
Solve the least squares problems is to find an approximate solution 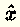\( \hat x \) such that the distance between the vectors \( Ax \) and \( B \) given by 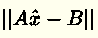\( || A\hat x - B || \) is the smallest.
It is shown in Linear Algebra and its Applications that the approximate solution 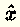\( \hat x \) is given by the equation
\[ R \hat x = Q^T B \]
where \( R \) and \( Q \) are such that \( A = Q R \) is the \( QR \) decomposition
of matrix \( A \); \( Q^T\) is the transpose of matrix \( Q \) and \( R \) is an upper triangualar matrix.
Note that this method
Examples with Solutions
Example 1
Use the \( QR \) decomposition to solve the least square problem related to the inconsistent system \( A x = B \) with
\( A =
\begin{bmatrix}
2 & 0 \\
0 & 1 \\
1 & 2
\end{bmatrix}
\) and \( B =
\begin{bmatrix}
1 \\
0 \\
3
\end{bmatrix}
\).
Solution to Example 1
Given
\( A =
\begin{bmatrix}
2 & 0 \\
0 & 1 \\
1 & 2
\end{bmatrix}
\)
Use the Gram-Schmidt process to find the orthogonal matrix \( Q \) and decompose matrix \( A \) as \( A = QR \).
\( Q =
\begin{bmatrix}
\dfrac{2\sqrt{5}}{5}&\dfrac{-4\sqrt{105}}{105}\\
0&\dfrac{\sqrt{105}}{21}\\
\dfrac{\sqrt{5}}{5}&\dfrac{8\sqrt{105}}{105}
\end{bmatrix}
\)
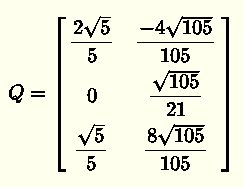We now calculate matrix \( R \).
Multiply both sides of \( A = QR \) by \( Q^T\) where \( Q^T \) is the transpose of \( Q \).
\( Q^T A = Q^T Q R \)
One of the properties of orthogonal matrices \( Q \) is that \( Q^T Q = I\), hence the above simplifies to
\( R = Q^T A \)
\( Q^T =
\begin{bmatrix}
\dfrac{2\sqrt{5}}{5} & 0 & \dfrac{\sqrt{5}}{5}\\
\dfrac{-4\sqrt{105}}{105} & \dfrac{\sqrt{105}}{21} & \dfrac{8\sqrt{105}}{105}
\end{bmatrix}
\)
Calculate \( R \)
\( R = Q^T A =
\begin{bmatrix}
\dfrac{2\sqrt{5}}{5} & 0 & \dfrac{\sqrt{5}}{5}\\
\dfrac{-4\sqrt{105}}{105} & \dfrac{\sqrt{105}}{21} & \dfrac{8\sqrt{105}}{105}
\end{bmatrix}
\begin{bmatrix}
2 & 0 \\
0 & 1 \\
1 & 2
\end{bmatrix}
=
\begin{bmatrix}
\sqrt{5}&\frac{2}{\sqrt{5}}\\
0 & \sqrt{\frac{21}{5}}
\end{bmatrix}
\)
Calculate \( Q^T B \)
\( Q^T B
=
\begin{bmatrix}
\dfrac{2\sqrt{5}}{5} & 0 & \dfrac{\sqrt{5}}{5}\\
\dfrac{-4\sqrt{105}}{105} & \dfrac{\sqrt{105}}{21} & \dfrac{8\sqrt{105}}{105}
\end{bmatrix}
\begin{bmatrix}
1 \\
0 \\
3
\end{bmatrix}
=
\begin{bmatrix}
\sqrt{5}\\
\dfrac{4\sqrt{5}}{\sqrt{21}}
\end{bmatrix}
\)
We now substitute \( R \) and \( Q^T B \) by their numerical values in the equation \( R \hat x = Q^T B \) and write the system
\( \begin{bmatrix}
\sqrt{5} & \dfrac{2}{\sqrt{5}}\\
0 & \sqrt{\dfrac{21}{5}}
\end{bmatrix} \cdot \hat x =
\begin{bmatrix}
\sqrt{5}\\
\dfrac{4\sqrt{5}}{\sqrt{21}}
\end{bmatrix}
\)
Solve the above using any method to obtain
\( \hat x =
\begin{bmatrix}
\dfrac{13}{21}\\
\dfrac{20}{21}
\end{bmatrix}
\)
Note that since matrix \( R \) is an upper triangular matrix, using the method of back substitution to solve the system \( R \hat x = Q^T B \) is the most efficient.
Example 2
Use the \( QR \) decomposition to solve the least square problem related to the inconsistent system \( A x = B \) with
\( A =
\begin{bmatrix}
1 & 0 & 1\\
2 & 0 & 0 \\
0 & -1 & 1\\
0 & -2 & 0
\end{bmatrix}
\) and \( B =
\begin{bmatrix}
2 \\
3 \\
4 \\
7
\end{bmatrix}
\).
Solution to Example 2
Given
\( A =
\begin{bmatrix}
1 & 0 & 1\\
2 & 0 & 0 \\
0 & -1 & 1\\
0 & -2 & 0
\end{bmatrix}
\)
Use the Gram-Schmidt process to find the orthogonal matrix \( Q \) and decompose matrix \( A \) as \( A = QR \).
\( Q =
\begin{bmatrix}
\dfrac{\sqrt{5}}{5} & 0 & \dfrac{\sqrt{10}}{5}\\
\dfrac{2\sqrt{5}}{5} & 0 & -\dfrac{\sqrt{10}}{10}\\
0&-\dfrac{\sqrt{5}}{5} & \dfrac{\sqrt{10}}{5}\\
0&-\dfrac{2\sqrt{5}}{5} & -\dfrac{\sqrt{10}}{10}
\end{bmatrix}
\)
We now calculate matrix \( R \). Multiply both sides of \( A = QR \) by \( Q^T\) where \( Q^T \) is the transpose of \( Q \).
\( Q^T A = Q^T Q R \)
One of the properties of orthogonal matrices \( Q \) is that \( Q^T Q = I\), hence the above simplifies to
\( R = Q^T A \)
\( Q^T =
\begin{bmatrix}
\dfrac{\sqrt{5}}{5}&\dfrac{2\sqrt{5}}{5}&0&0\\
0&0&-\dfrac{\sqrt{5}}{5}&-\dfrac{2\sqrt{5}}{5}\\
\dfrac{\sqrt{10}}{5}&-\dfrac{\sqrt{10}}{10}&\dfrac{\sqrt{10}}{5}&-\dfrac{\sqrt{10}}{10}
\end{bmatrix}
\)
Calculate \( R \)
\( R = Q^T A =
\begin{bmatrix}
\dfrac{\sqrt{5}}{5}&\dfrac{2\sqrt{5}}{5}&0&0\\
0&0&-\dfrac{\sqrt{5}}{5}&-\dfrac{2\sqrt{5}}{5}\\
\dfrac{\sqrt{10}}{5}&-\dfrac{\sqrt{10}}{10}&\dfrac{\sqrt{10}}{5}&-\dfrac{\sqrt{10}}{10}
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 1\\
2 & 0 & 0 \\
0 & -1 & 1\\
0 & -2 & 0
\end{bmatrix}
=
\begin{bmatrix}
\sqrt{5} & 0 & \dfrac{1}{\sqrt{5}}\\
0 & \sqrt{5} & -\dfrac{1}{\sqrt{5}}\\
0 & 0 & \dfrac{2 \sqrt 2}{\sqrt{5}}
\end{bmatrix}
\)
Calculate \( Q^T B \)
\( Q^T B
=
\begin{bmatrix}
\dfrac{\sqrt{5}}{5}&\dfrac{2\sqrt{5}}{5} & 0 & 0\\
0 & 0 & -\dfrac{\sqrt{5}}{5} & -\dfrac{2\sqrt{5}}{5}\\
0 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
2 \\
3 \\
4 \\
7
\end{bmatrix}
=
\begin{bmatrix}
\frac{8}{\sqrt{5}}\\
-\frac{18}{\sqrt{5}}\\
\sqrt{\frac{2}{5}}
\end{bmatrix}
\)
We now substitute \( R \) and \( Q^T B \) by their numerical values in the equation \( R \hat x = Q^T B \) and write the system
\( \begin{bmatrix}
\begin{bmatrix}
\sqrt{5} & 0 & \dfrac{1}{\sqrt{5}}\\
0 & \sqrt{5} & -\dfrac{1}{\sqrt{5}}\\
0 & 0 & \dfrac{2}{\sqrt{5}}
\end{bmatrix}
\end{bmatrix}
\cdot
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
=
\begin{bmatrix}
\frac{8}{\sqrt{5}}\\
-\frac{18}{\sqrt{5}}\\
\sqrt{\frac{2}{5}}
\end{bmatrix}
\)
Solve to obtain
\( x_1 = \dfrac{3}{2} \) , \( x_2 = \dfrac{-7}{2} \) , \( x_3 = \dfrac{1}{2} \)
\( \hat x =
\begin{bmatrix}
\dfrac{3}{2} \\
\dfrac{-7}{2}\\
\dfrac{1}{2}
\end{bmatrix}
\)
More References and links
- Vector Spaces - Questions with Solutions
- Solve Least Squares Problems by the Normal Equations.
- Linear Algebra and its Applications - 5 th Edition - David C. Lay , Steven R. Lay , Judi J. McDonald
- Elementary Linear Algebra - 7 th Edition - Howard Anton and Chris Rorres
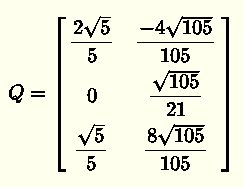