Least Square Problem

In many real life applications, when a solution x to a system of equations of the form A x = B cannot be found (i.e. the system is inconsistent), it is possible that an approximate solution to the given system A x = B is enough.
The least squares problems is to find an approximate solution such that the distance between the vectors A x and B given by is the smallest.
It is shown in Linear Algebra and its Applications that the approximate solution is given by the normal equation
where A^T is the transpose of matrix A .

Examples with Solutions

Example 1
a) Show that the system A x = B with 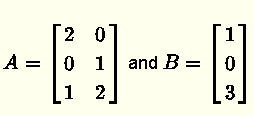is inconsistent (system with no solutions).
b) Find the least square solution to the inconsistent system A x = B .
c) Determine the least square error given by || A x = B || for the solution found in part b).

Solution to Example 1
a)
The system of equations to solve may be written in the form

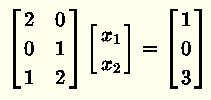
Write the above system in augmented matrix form

Row reduce (Gauss Jordan) the above augmented matrix
\( \) \( \) \( \) \( \)
The last row gives the equation \( 0 \cdot x_1 + 0 \cdot x_2 = 1 \) which has no solution and therefore the system is inconsistent.
b)
Let us find \( A^T \)
\( A^T = \begin{bmatrix} 2 & 0 & 1\\ 0 & 1 & 2 \end{bmatrix} \)
Calculate \( A^T A \) and \( A^T B \)
\( A^T A = \begin{bmatrix} 2 & 0 & 1\\ 0 & 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} 2 & 0 \\ 0 & 1 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} 5 & 2\\ 2 & 5 \end{bmatrix} \)

\( A^T B = \begin{bmatrix} 2 & 0 & 1\\ 0 & 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \\ 3 \end{bmatrix} = \begin{bmatrix} 5\\ 6 \end{bmatrix} \)
Substitute \( A^T A \) and \( A^T B \) by their numerical values in the normal equation \( A^T A \hat x = A^T B \), we obtain the system
\( \begin{bmatrix} 5 & 2\\ 2 & 5 \end{bmatrix} \cdot \hat x = \begin{bmatrix} 5\\ 6 \end{bmatrix} \)
Solve the above to obtain
\( \hat x = \begin{bmatrix} \dfrac{13}{21}\\ \dfrac{20}{21} \end{bmatrix} \)
c)
\( A \cdot \hat x - B = \begin{bmatrix} 2 & 0 \\ 0 & 1 \\ 1 & 2 \end{bmatrix} \begin{bmatrix} \dfrac{13}{21}\\ \dfrac{20}{21} \end{bmatrix} - \begin{bmatrix} 1 \\ 0 \\ 3 \end{bmatrix} = \begin{bmatrix} \dfrac{5}{21}\\ \dfrac{20}{21}\\ - \dfrac{10}{21}\end{bmatrix} \)

\( || A \cdot \hat x - B || = \sqrt { (\dfrac{5}{21})^2 + (\dfrac{20}{21})^2 + (- \dfrac{10}{21})^2 } = \dfrac{5\sqrt{21}}{21} \approx 1.1 \)

Example 2
a) Show that the system \( A x = B \) with \( A = \begin{bmatrix} 1 & 0 & 1\\ 2 & 0 & 2 \\ 0 & -1 & 1\\ 0 & -2 & 2 \end{bmatrix} \) and \( B = \begin{bmatrix} 2 \\ 3 \\ 4 \\ 7 \end{bmatrix} \) is inconsistent.
b) Find the least square solution to the inconsistent system \( A x = B \).
c) Determine the least square error given by \( || Ax - B || \) for the solution found in part b).

Solution to Example 2
a)
The system of equations to solve may be written in the form
\[ \begin{bmatrix} 1 & 0 & 1\\ 2 & 0 & 2 \\ 0 & -1 & 1\\ 0 & -2 & 2 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \\ 4 \\ 7 \end{bmatrix} \]
Write the above system in augmented matrix form
\( \begin{bmatrix} 1 & 0 & 1 & |& 2\\ 2 & 0 & 2 & | & 3 \\ 0 & -1 & 1 & | & 4 \\ 0 & -2 & 2 & | & 7 \end{bmatrix} \)
Write in row reduced form (Gauss - Jordan)
\( \begin{bmatrix} 1 & 0 & 1 & | & 0\\ 0 & 1 & -1 & | & 0 \\ 0 & 0 & 0 & | & 1 \\ 0 & 0 & 0 & | & 0 \end{bmatrix} \)
The third row gives the equation \( 0 \cdot x_1 + 0 \cdot x_2 + 0 \cdot x_3 = 1 \) which has no solution and therefore the system is inconsistent.
b)
Let us first find \( A^T \)
\( A^T = \begin{bmatrix} 1 & 2 & 0 & 0\\ 0 & 0 & -1 & -2\\ 1 & 2 & 1 & 2 \end{bmatrix} \)
Calculate \( A^T A \) and \( A^T B \)
\( A^T A = \begin{bmatrix} 1 & 2 & 0 & 0\\ 0 & 0 & -1 & -2\\ 1 & 2 & 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 1\\ 2 & 0 & 2 \\ 0 & -1 & 1\\ 0 & -2 & 2 \end{bmatrix} = \begin{bmatrix} 5 & 0 & 5\\ 0 & 5 & -5\\ 5 & -5 & 10 \end{bmatrix} \)

\( A^T B = \begin{bmatrix} 1 & 2 & 0 & 0\\ 0 & 0 & -1 & -2\\ 1 & 2 & 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 3 \\ 4 \\ 7 \end{bmatrix} = \begin{bmatrix} 8\\ -18\\ 26 \end{bmatrix} \)
Substitute \( A^T A \) and \( A^T B \) by their numerical values in the normal equation \( A^T A \hat x = A^T B \), we obtain the system
\( \begin{bmatrix} 5 & 0 & 5\\ 0 & 5 & -5\\ 5 & -5 & 10 \end{bmatrix} \cdot \hat x = \begin{bmatrix} 8\\ -18\\ 26 \end{bmatrix} \)
Write the above system in augmented matrix form
\( \begin{bmatrix} 5 & 0 & 5 & | & 8\\ 0 & 5 & -5 & | & -18\\ 5 & -5 & 10 & | & 26 \end{bmatrix} \)
Row reduce the above matrix
\( \begin{bmatrix} 1 & 0 & 1 & | & \dfrac{8}{5}\\ 0 & 1 & -1 & | & -\dfrac{18}{5}\\ 0 & 0 & 0 & | & 0 \end{bmatrix} \)
\( x_3 \) is the free variable.
second row gives: \( x_2 - x_3 = -\dfrac{18}{5} \) hence \( x_2 = x_3 -\dfrac{18}{5} \)
first row gives: \( x_1 + x_3 = \dfrac{8}{5} \) hence \( x_1 = - x_3 + \dfrac{8}{5} \)
The solution is given by
\( \hat x = \begin{bmatrix} -x_3 + \dfrac{8}{5}\\ x_3 -\dfrac{18}{5}\\ x_3 \end{bmatrix} \) with \( x_3 \in \mathbb{R} \)
Note that there is an infinite number of solutions to this least square problem. c)
\( A \cdot \hat x - B = \begin{bmatrix} 1 & 0 & 1\\ 2 & 0 & 2 \\ 0 & -1 & 1\\ 0 & -2 & 2 \end{bmatrix} \begin{bmatrix} -x_3 + \dfrac{8}{5}\\ x_3 -\dfrac{18}{5}\\ x_3 \end{bmatrix} - \begin{bmatrix} 2 \\ 3 \\ 4 \\ 7 \end{bmatrix} = \begin{bmatrix} -\dfrac{2}{5}\\ \dfrac{1}{5}\\ -\dfrac{2}{5}\\ \dfrac{1}{5} \end{bmatrix} \)
\( || A \cdot \hat x - B || = \sqrt { (-\dfrac{2}{5})^2 + (\dfrac{1}{5})^2 + (-\dfrac{2}{5})^2 + (\dfrac{1}{5})^2} = \dfrac{\sqrt{2}}{5} \approx 0.63 \)
Note that the least square error \( || Ax - B || \) is constant and does not depend on \( x_3 \).

More References and links

1. Vector Spaces - Questions with Solutions
2. Solve Least Squares Problems by the QR Decomposition
3. Linear Algebra and its Applications - 5 th Edition - David C. Lay , Steven R. Lay , Judi J. McDonald
4. Elementary Linear Algebra - 7 th Edition - Howard Anton and Chris Rorres