Find Matrix Inverse Using Row Operations

Introduction

We present examples on how to find the inverse of a matrix using the three row operations listed below:

  1. Interchange two rows
  2. Add a multiple of one row to another
  3. Multiply a row by a non zero constant
Examples with detailed solutions are also included.
An Inverse of a Matrix Using Row Reduction - Calculator - Calculator

Inverse of a Matrix

Let A be an n × n matrix. If matrix A-1 is the inverse of matrix A , then we have

A A-1 = In = A-1 A

where In is the n × n identity matrix
Consider the matrix equation A A-1 = In where A-1 is the unknown. To find the inverse A-1 , we start with the augmented matrix [ A | In ] and then row reduce it. If matrix A is invertible, the row reduction will end with an augmented matrix in the form

[ In | A-1 ]

where the inverse A-1 is the n × n on the right side of the augmented matrix [ In | A-1 ].


Examples with Solutions

Example 1
Find the inverse of matrix 2 by 2 Square Matrix

Solution to Example 1
Write the augmented matrix [ A | I2 ]
Augmented Matrix
Let R1 and R2 be the first and the second rows of the above augmented matrix.
Write the above augmented matrix in reduced row echelon form .
Rows Operations
The above augmented matrix has the form [ I2 | A-1 ] and therefore A-1 is given by
Inverse Matrix



Example 2
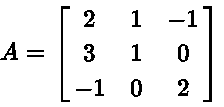
Find the inverse of matrix 3 by 3 Matrix

Solution to Example 2
Write the augmented matrix [ A | I3 ]
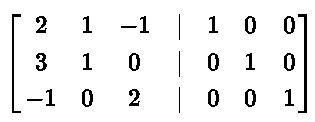
Augmented Matrix

Let R1, R2 and R3 be the first, the second and the third rows respectively of the above augmented matrix.
Write the above augmented matrix in reduced row echelon form .
Row Reduce Steps \( \)\( \)\( \)

The above augmented matrix has the form \( [ I_3 | A^{-1} ] \) and therefore \( A^{-1} \) is given by
\( A^{-1} = \begin{bmatrix} -\frac{2}{3} & \frac{2}{3} & -\frac{1}{3} \\ 2 & -1 & 1 \\ -\frac{1}{3} & \frac{1}{3} & \frac{1}{3} \end{bmatrix} \)



Example 3
Find the inverse of matrix \( A = \begin{bmatrix} 0 & 1 & -1 & 1\\ 2 & 2 & 0 & -2\\ 1 & 1 & -2 & 0 \\ 0 & 1 & 2 & 0 \end{bmatrix} \).

Solution to Example 3
Write the augmented matrix \( [ A | I_4 ] \)
\( \begin{bmatrix} 0 & 1 & -1 & 1 & | & 1 & 0 & 0 & 0\\ 2 & 2 & 0 & -2 & | & 0 & 1 & 0 & 0 \\ 1 & 1 & -2 & 0 & | & 0 & 0 & 1 & 0\\ 0 & 1 & 2 & 0 & | & 0 & 0 & 0 & 1 \\ \end{bmatrix} \)
Write the above augmented matrix in reduced row echelon form .
Interchange \( R_1 \) and \( R_3 \)
Interchange Rows of Matrix

Interchange \( R_2 \) and \( R_4 \)
Interchange Rows of Matrix
The above augmented matrix has the form \( [ I_4 | A^{-1} ] \) and therefore \( A^{-1} \) is given by
\( A^{-1} = \begin{bmatrix} -4 & -2 & 5 & 3 \\ 2 & 1 & -2 & -1 \\ -1 & -1/2 & 1 & 1 \\ -2 & -3/2 & 3 & 2 \end{bmatrix} \)



Example 4
Find the inverse of matrix \( A = \begin{bmatrix} 1 & 2 & 0\\ 0 & 1 & 3 \\ 1 & 4 & 6 \end{bmatrix} \).

Solution to Example 4
Write the augmented matrix \( [ A | I_3 ] \)
\( \begin{bmatrix} 1 & 2 & 0 & | & 1 & 0 & 0\\ 0 & 1 & 3 & | & 0 & 1 & 0\\ 1 & 4 & 6 & | & 0 & 0 & 1 \end{bmatrix} \)
Write the above augmented matrix in reduced row echelon form .
\( \begin{matrix} \\ \\ \color{red}{R_3 - R_1}\\ \end{matrix} \begin{bmatrix} 1 & 2 & 0 & | & 1 & 0 & 0\\ 0 & 1 & 3 & | & 0 & 1 & 0\\ 0 & 2 & 6 & | & -1 & 0 & 1 \\ \end{bmatrix} \)

\( \begin{matrix} \\ \\ \color{red}{R_3 - 2 R_2}\\ \end{matrix} \begin{bmatrix} 1 & 2 & 0 & | & 1 & 0 & 0\\ 0 & 1 & 3 & | & 0 & 1 & 0\\ 0 & 0 & 0 & | & -1 & -2 & 1 \\ \end{bmatrix} \)

The last row of the original matrix (on the left side) is all zeros and therefore the rows in the orgiginal matrix \( A \) are not linearly independent and hence the given matrix is NOT invertible.



More References and links

  1. matrix inverse
  2. linear algebra
  3. identity matrix
  4. Find the Inverse of a Matrix Using Row Reduction - Calculator - Calculator
  5. Solve a system of linear equations by elimination
  6. elementary matrices
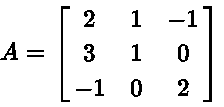
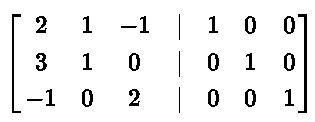