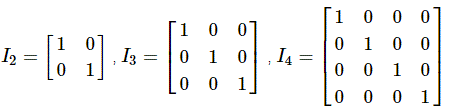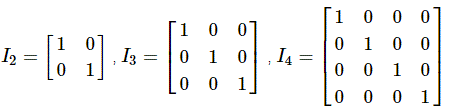Inverse Matrix Questions with Solutions
Tutorials including examples and questions with detailed solutions on how to find the inverse of square matrices
using the method of the row echelon form and the method of cofactors. The properties of inverse matrices are discussed and various questions, including some challenging ones, related to inverse matrices are included along with their detailed solutions.
Page Content
The identity matrix I n is the square matrix with order n x n and with the elements in the main diagonal consisting of 1's and all other elements are equal to zero.
Examples of indentity matrices
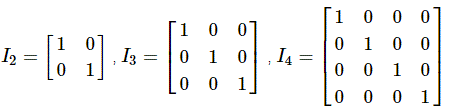
Definition of The Inverse of a Matrix
Let A be a square matrix of order n x n. If there exists a matrix B of the same order such that
A B = I n = B A
where I n is the identity matrix of order n x n, then B is called the inverse matrix of A and matrix A is the inverse matrix of B.
Example 1
Verify that matrices A and B given below are inverses of each other.

Solution
Let us find the products AB and BA

AB = BA = I 2 and therefore A and B are inverse of each other.
The inverse of a square matrix A is denoted as A -1 and is unique.
Find the Inverse of a Square Matrix Using the Row Reduction Method
This method is also called Gauss–Jordan elimination method.
We first write the augmented matrix
\( \) \( \) \( \) \( \)
\[ [ A | I ] \]
where I is the identity matrix of the same order as matrix A and then use row elementary operations to rewrite it as
\[ [ I | A^{-1} ] \]
where \( A^{-1} \) is the inverse of matrix A.
An online calculator to find the inverse of a matrix using row reduction is included.
Example 2
Find the inverse of matrix A given by
\[ A = \begin{bmatrix}
1&1 \\ 2&4
\end{bmatrix} \]
if it exists.
Solution
Write the augmented matrix \( [ A | I )\)
\[ \begin{bmatrix}
1&1&|&1&0\\2&4&|&0&1
\end{bmatrix} \]
step 1
\[
\color{red}{\begin{matrix}
\\
R_2 - 2 \times R_1
\end{matrix} }
\begin{bmatrix}
1&1&|&1&0\\0&2&|&-2&1
\end{bmatrix} \]
step 2
\[
\color{red}{\begin{matrix}
\\
(1/2)R_2
\end{matrix} }
\begin{bmatrix}
1&1&|&1&0\\0&1&|&-1&1/2
\end{bmatrix} \]
step 3
\[
\color{red}{\begin{matrix}
R_1 - R_2 \\
\\
\end{matrix} }
\begin{bmatrix}
1&0&|&2&-1/2\\0&1&|&-1&1/2
\end{bmatrix} \]
The inverse of A is the 2 × 2 matrix on the right side given by
\[ A^{-1} =
\begin{bmatrix}
2&-1/2\\-1&1/2
\end{bmatrix} \]
Example 3
Find the inverse of matrix A given by
\[
A = \begin{bmatrix}-2&2&0 \\ 2&1&3\\ -2&4&-2\end{bmatrix}
\]
if it exists.
Solution
Write the augmented matrix \( [ A | I )\)
\[ \begin{bmatrix}
-2&2&0&|&1&0&0\\
2&1&3&|&0&1&0 \\
-2 & 4 & -2 &|& 0 & 0 & 1
\end{bmatrix} \]
step 1
\[
\color{red}{ \begin{matrix}
\\
R_2 + R_1 \\
R_3 - R_1
\end{matrix} }
\begin{bmatrix}
-2&2&0&|&1&0&0\\
0&3&3&|&1&1&0 \\
0 & 2 & -2 &|& -1 & 0 & 1
\end{bmatrix}
\]
step 2
\[
\color{red}{ \begin{matrix}
\\
\\
R_3 - (2/3) R_2 \\
\end{matrix} }
\begin{bmatrix}
-2&2&0&|&1&0&0\\
0&3&3&|&1&1&0 \\
0 & 0 & - 4&|& -5/3 & -2/3 & 1
\end{bmatrix} \]
step 3
\[
\color{red}{
\begin{matrix}
\\
\\
(-1/4)R_3 \\
\end{matrix}}
\begin{bmatrix}
-2&2&0&|&1&0&0\\
0&3&3&|&1&1&0 \\
0 & 0 & 1&|& 5/12 & 1/6 & -1/4
\end{bmatrix} \]
step 4
\[
\color{red}{
\begin{matrix}
\\
R_2 - 3\times R_3 \\
\\
\end{matrix} }
\begin{bmatrix}
-2&2&0&|&1&0&0\\
0&3&0&|&-1/4&1/2&3/4 \\
0 & 0 & 1&|& 5/12 & 1/6 & -1/4
\end{bmatrix} \]
step 5
\[
\color{red}{
\begin{matrix}
\\
(1/3) R_2 \\
\\
\end{matrix}}
\begin{bmatrix}
-2&2&0&|&1&0&0\\
0&1&0&|&-1/12&1/6&1/4 \\
0 & 0 & 1&|& 5/12 & 1/6 & -1/4
\end{bmatrix} \]
step 6
\[
\color{red}{
\begin{matrix}
R_1- 2\times R_2 \\
\\
\\
\end{matrix} }
\begin{bmatrix}
-2&0&0&|&7/6&-1/3&-1/2\\
0&1&0&|&-1/12&1/6&1/4 \\
0 & 0 & 1&|& 5/12 & 1/6 & -1/4
\end{bmatrix} \]
step 7
\[
\color{red}{
\begin{matrix}
(-1/2) R_1 \\
\\
\\
\end{matrix} }
\begin{bmatrix}
1&0&0&|&-7/12&1/6&1/4\\
0&1&0&|&-1/12&1/6&1/4 \\
0 & 0 & 1&|& 5/12 & 1/6 & -1/4
\end{bmatrix} \]
Hence
\[ A^{-1} =
\begin{bmatrix}
-7/12&1/6&1/4\\
-1/12&1/6&1/4 \\
5/12 & 1/6 & -1/4
\end{bmatrix} \]
More examples on how to find matrix inverse using row operations are included.
Find the Inverse of a Square Matrix Using Minors, Cofactors and Adjugate
This method is explained using a numerical example. Matrix A is given below.
\[ A = \begin{bmatrix}
-1&0&1\\
2&-1&2 \\
-1 & 2 & 1
\end{bmatrix} \]
a) Find the matrices of minors and cofactors, the adjugate and the inverse of A.
Matrix of Minors
The entry \( M_{i,j} \) of the matrix of minors of matrix A is given by the determinant obtained by deleting the \( i^{th}\) row and the \( j^{th}\) column.
To find \( M_{1,1} \), delete row 1 and column 1 from matrix A and find the determinant of the remaining 2 by 2 matrix as follows:
\( M_{1,1} = Det \begin{bmatrix}
.&.&.\\
.&-1&2 \\
.& 2 & 1
\end{bmatrix} = -1 - 4 = -5\)
To find \( M_{1,2} \), delete row 1 and column 2 from matrix A and find the determinant of the remaining 2 by 2 matrix as follows:
\( M_{1,2} = Det \begin{bmatrix}
.&.&.\\
2&.&2 \\
-1 & . & 1
\end{bmatrix} = 2 -(-2) = 4 \)
To find \( M_{1,3} \), delete row 1 and column 3 from matrix A and find the determinant of the remaining 2 by 2 matrix as follows:
\( M_{1,3} = Det \begin{bmatrix}
.&.&.\\
2&-1&. \\
-1 & 2 & .
\end{bmatrix} = 4 - 1 = 3 \)
To find \( M_{2,1} \), delete row 2 and column 1 from matrix A and find the determinant of the remaining 2 by 2 matrix as follows:
\( M_{2,1} = Det \begin{bmatrix}
.&0&1\\
.&.&. \\
. & 2 & 1
\end{bmatrix} = 0 - 2 = - 2 \)
...
...
The remaining entries are given by:
\( M_{2,2} = 0 \) , \( M_{2,3} = -2 \) , \( M_{3,1} = 1\) , \( M_{3,2} = -4\) , \( M_{3,3} = 1\).
The matrix of minors M is given by
\( M = \begin{bmatrix} -5&4&3\\ -2&0&-2\\ 1&-4&1 \end{bmatrix} \)
Matrix of Cofactors
The entries \( C_{i,j} \) of the matrix of cofactors C of matrix A are given by
\( C_{i,j} = (-1)^{i+j}M{i,j} \)
An evaluation of the entries \( C_{i,j} \) gives:
\( C_{1,1} = (-1)^{1+1} M_{1,1} = -5 \)
\( C_{1,2} = (-1)^{1+2} M_{1,2} = - 4 \)
\( C_{1,3} = (-1)^{1+3} M_{1,3} = 3 \)
\( C_{2,1} = (-1)^{2+1} M_{2,1} = 2 \)
\( C_{2,2} = (-1)^{2+2} M_{2,2} = 0 \)
\( C_{3,1} = (-1)^{3+1} M_{3,1} = 1 \)
\( C_{3,2} = (-1)^{3+2} M_{3,2} = 4 \)
\( C_{3,3} = (-1)^{3+3} M_{3,1} = 1 \)
Hence the matrix C of cofactors is given by
\( C = \begin{bmatrix} -5&-4&3\\ 2&0&2\\ 1&4&1 \end{bmatrix} \)
Adjugate (or adjunct) of a Matrix
The adjugate (or adjunct) of matrix A is the transpose of its matrix of cofactors C.
\( Adjugate(A) = C^T = \begin{bmatrix} -5&2&1\\ -4&0&4\\ 3&2&1 \end{bmatrix} \)
Inverse Matrix
We now need to find the determinant D of matrix A.
Using the first row of matrix A and the corresponding minors already found, D is given by
\( D = det\begin{bmatrix}
-1&0&1\\
2&-1&2 \\
-1 & 2 & 1
\end{bmatrix} = A_{11}M_{1,1} - A_{1,2}M_{1,2} + A_{1,3}M_{1,3} = 8\)
The inverse of \( A \) is given by
\( A^{-1} = \dfrac{1}{D} C^T = \dfrac{1}{8} \begin{bmatrix} -5&2&1\\ -4&0&4\\ 3&2&1 \end{bmatrix} = \begin{bmatrix} -\dfrac{5}{8}&\dfrac{1}{4}&\dfrac{1}{8}\\ -\dfrac{1}{2}&0&\dfrac{1}{2}\\ \dfrac{3}{8}&\dfrac{1}{4}&\dfrac{1}{8}\end{bmatrix}\)
Formula for the Inverse of a 2 by 2 Matrix
Using any of the two methods described above, it can be shown that the inverse of matrix A given by
\[ A = \begin{bmatrix}
a & b\\
c & d \\
\end{bmatrix} \]
is given by
\[ A^{-1} = \dfrac{1}{ad - bc}\begin{bmatrix}
d & -b\\
-c & a \\
\end{bmatrix} \]
Properties of Inverse Matrices
A matrix that has an inverse is called an invertible matrix.
- If A is an invertible matrix, its inverse is unique.
- \( A A^{-1} = A^{-1} A = I \)
- If matrices A and B are invertible, then:\( (AB)^{-1} = B^{-1}A^{-1} \)
- A matrix is invertible if and only if its determinant is not equal to zero.
- A matrix whose determinant is not equal to zero is called nonsingular.
- \( (A^T)^{-1} = (A^{-1})^T \)
- \( Det(A^{-1}) = \dfrac{1}{Det(A)} \)
- \( (A^{-1})^{-1} = A \)
Questions on Inverse Matrices
- Question 1
Use row reduction method to find the inverse of the following matrices:
\( A =
\begin{bmatrix}
-1&-1&1\\
2&0&-2 \\
1 & 1 & 1
\end{bmatrix} \)
,
\( B =
\begin{bmatrix}
1&0&1&2\\
-1& 1 & 2 & 0 \\
-2& 0 & 1 & 2 \\
0 & 0 & 0 & 1
\end{bmatrix} \)
- Question 2
Use the method of cofactors to find the inverse of the following matrix.
\( A =
\begin{bmatrix}
-1&0&3\\
3&2&2 \\
0& 0 & 1
\end{bmatrix} \)
- Question 3
A, B and C are 2 by 2 matrices. Matrices B and C are given by:
\[ B =
\begin{bmatrix}
-1&-1\\
-2& 1
\end{bmatrix} , C =
\begin{bmatrix}
2 & -1\\
-2 & 2
\end{bmatrix} \]
Find matrix A such that AB = C.
- Question 4
For what value(s) of k is each of the matrices given below invertible?
a) \(
\begin{bmatrix}
k & -1 & 4\\
2 & 0 & 1\\
-1 & 0 & -1
\end{bmatrix} \) , b) \( \begin{bmatrix}
k & -1 \\
-1 & 3
\end{bmatrix} \) , c) \(
\begin{bmatrix}
k & -1 & 4\\
0 & k + 1 & 1\\
0 & 0 & k -3
\end{bmatrix} \)
- Question 5
The square matrices P, Q, R and S are of the same dimension and invertible such that
\[ P = Q R^{-1} S \]
Express (or determine) \( R\) in terms of \( P \), \( Q\) and \( S \) or/and their inverses.
- Question 6
Matrix A is given by
\( A =
\begin{bmatrix}
a & 0 & 0 & 0\\
0 & b & 0 & 0 \\
0 & 0 & c & 0\\
0 & 0 & 0 & d
\end{bmatrix} \)
Find a formula for the inverse of matrix A if none of the parameters a, b, c and d is equal to zero.
- Question 7
Use the inverse matrix to solve the system of equations
\(
\begin{bmatrix}
1&0&1&2\\
-1& 1 & 2 & 0 \\
-2& 0 & 1 & 2 \\
0 & 0 & 0 & 1
\end{bmatrix}\begin{bmatrix}
x_1\\
x_2 \\
x_3\\
x_4
\end{bmatrix} = \begin{bmatrix}
0\\
1 \\
-1\\
2
\end{bmatrix}
\)
- Question 8
What is the most efficient method to solve the following systems of equations?
\( A X_1 = B_1 \) , \( A X_2 = B_2 \) , \( A X_3 = B_3 \) ... \( A X_i = B_i \)
- Question 9
A and B are invertible matrices of the same dimension related by: \( A^{-1} = A B \).
Find B in terms of A or its inverse.
- Question 10
1) Give an example of 2 by 2 matrices A and B such that neither A nor B are invertible yet A + B is invertible.
2) Give an example of 2 by 2 matrices A and B such that neither A nor B are invertible yet A - B is invertible.
- Question 11
Use any of the two methods to find a formula for the inverse of a 2 by 2 matrix.(It is already given above without proof).
- Question 12
The system of equations in matrix form
\( A X = B \)
has the following solutions:
\( X_1 = \begin{bmatrix}
-1\\
2 \\
3
\end{bmatrix}
\) for \( B_1 = \begin{bmatrix}
2\\
13 \\
3
\end{bmatrix} \) , \( X_2 = \begin{bmatrix}
0\\
-1 \\
1
\end{bmatrix}
\) for \( B_2 = \begin{bmatrix}
4\\
2 \\
2
\end{bmatrix} \) ,
\( X_3 = \begin{bmatrix}
1\\
1 \\
1
\end{bmatrix}
\) for \( B_3 = \begin{bmatrix}
4\\
5 \\
3
\end{bmatrix} \).
Find X for \( B = \begin{bmatrix}
1\\
-9 \\
-1
\end{bmatrix} \).
Solutions to the Above Questions
- Solution to Question 1
Inverse of matrix A
Write the augmented matrix \( [ A | I ] \)
\[ \begin{bmatrix}
-1&-1&1&|&1&0&0\\
2&0&-2&|&0&1&0 \\
1 & 1 & 1 &|& 0 & 0 & 1
\end{bmatrix} \]
step 1
\[
\color{red}{ \begin{matrix}
-R_1\\
\\
\\
\end{matrix} }
\begin{bmatrix}
1&1&-1&|&-1&0&0\\
2&0&-2&|&0&1&0 \\
1 & 1 & 1 &|& 0 & 0 & 1
\end{bmatrix}
\]
step 2
\[
\color{red}{ \begin{matrix}
\\
R_2-2R_1 \\
\\
\end{matrix} }
\begin{bmatrix}
1&1&-1&|&-1&0&0\\
0&-2&0&|&2&1&0 \\
1 & 1 & 1 &|& 0 & 0 & 1
\end{bmatrix} \]
step 3
\[
\color{red}{ \begin{matrix}
\\
\\
R_3-R_1\\
\end{matrix} }
\begin{bmatrix}
1&1&-1&|&-1&0&0\\
0&-2&0&|&2&1&0 \\
0 & 0 & 2 &|& 1 & 0 & 1
\end{bmatrix} \]
step 4
\[
\color{red}{ \begin{matrix}
\\
R_2=(-1/2)R_2\\
R_3=(1/2)R_3\\
\end{matrix} }
\begin{bmatrix}
1&1&-1&|&-1&0&0\\
0&1&0&|&-1&-1/2&0 \\
0 & 0 & 1 &|& 1/2 & 0 & 1/2
\end{bmatrix} \]
step 5
\[
\color{red}{ \begin{matrix}
R_1+R_3\\
\\
\\
\end{matrix} }
\begin{bmatrix}
1&1&0&|&-1/2&0&1/2\\
0&1&0&|&-1&-1/2&0 \\
0 & 0 & 1 &|& 1/2 & 0 & 1/2
\end{bmatrix} \]
step 6
\[
\color{red}{ \begin{matrix}
R_1-R_2\\
\\
\\
\end{matrix} }
\begin{bmatrix}
1&0&0&|&1/2&1/2&1/2\\
0&1&0&|&-1&-1/2&0 \\
0 & 0 & 1 &|& 1/2 & 0 & 1/2
\end{bmatrix} \]
The inverse of matrix A is the 3 by 3 matrix on the right side. Hence
\[ A^{-1} = \begin{bmatrix}
1/2&1/2&1/2\\
-1&-1/2&0 \\
1/2 & 0 & 1/2
\end{bmatrix} \]
Inverse of matrix B
Write the augmented matrix \( [ B | I ] \)
\[ \begin{bmatrix}
1&0&1&2 & |&1&0&0&0\\
-1& 1 & 2 & 0 &|&0&1&0&0 \\
-2& 0 & 1 & 2 &|& 0 & 0 & 1 & 0\\
0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1
\end{bmatrix} \]
step 1
\[
\color{red}{ \begin{matrix}
\\
R_2+R_1\\
R_3+2R_1\\
\\
\end{matrix} }
\begin{bmatrix}
1&0&1&2 & |&1&0&0&0\\
0& 1 & 3 & 2 &|&1&1&0&0 \\
0& 0 & 3 & 6 &|& 2 & 0 & 1 & 0\\
0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1
\end{bmatrix}
\]
step 2
\[
\color{red}{ \begin{matrix}
\\
\\
(1/3) R_3\\
\\
\end{matrix} }
\begin{bmatrix}
1&0&1&2 & |&1&0&0&0\\
0& 1 & 3 & 2 &|&1&1&0&0 \\
0& 0 & 1 & 2 &|& 2/3 & 0 & 1/3 & 0\\
0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1
\end{bmatrix}
\]
step 3
\[
\color{red}{ \begin{matrix}
R_1-2R_4\\
R_2-2R_4\\
R_3-2R_4\\
\\
\end{matrix} }
\begin{bmatrix}
1&0&1&0 & |&1&0&0&-2\\
0& 1 & 3 & 0 &|&1&1&0&-2 \\
0& 0 & 1 & 0 &|& 2/3 & 0 & 1/3 & -2\\
0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1
\end{bmatrix}
\]
step 4
\[
\color{red}{ \begin{matrix}
R_1-R_3\\
R_2-3R_3\\
\\
\\
\end{matrix} }
\begin{bmatrix}
1&0&1&0 & |&1/3&0&-1/3&0\\
0& 1 & 0 & 0 &|&-1&1&-1&4 \\
0& 0 & 1 & 0 &|& 2/3 & 0 & 1/3 & -2\\
0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1
\end{bmatrix}
\]
The inverse of matrix B is the 4 by 4 matrix on the right side. Hence
\[ B^{-1} = \begin{bmatrix}
1/3&0&-1/3&0\\
-1&1&-1&4 \\
2/3 & 0 & 1/3 & -2\\
0 & 0 & 0 & 1
\end{bmatrix} \]
- Solution to Question 2
We first find the minors.
\( M_{1,1} = Det \begin{bmatrix}
.&.&.\\
.&2&2 \\
.& 0 & 1
\end{bmatrix} = 2\) ,
\( M_{1,2} = Det \begin{bmatrix}
.&.&.\\
3&.&2 \\
0& . & 1
\end{bmatrix} = 3\) ,
\( M_{1,3} = Det \begin{bmatrix}
.&.&.\\
3&2&. \\
0& 0 & .
\end{bmatrix} = 0 \)
\( M_{2,1} = Det \begin{bmatrix}
.&0&3\\
.&.&. \\
.& 0 & 1
\end{bmatrix} = 0\) ,
\( M_{2,2} = Det \begin{bmatrix}
-1&.&3\\
. & . & . \\
0& . & 1
\end{bmatrix} = -1\) ,
\( M_{2,3} = Det \begin{bmatrix}
-1&0&.\\
. & . & .\\
0& 0 & .
\end{bmatrix} = 0\)
\( M_{3,1} = Det \begin{bmatrix}
.&0&3\\
.&2&2 \\
. & . & .
\end{bmatrix} = - 6\) ,
\( M_{3,2} = Det \begin{bmatrix}
-1&.&3\\
3&.&2 \\
. & . & .
\end{bmatrix} = - 11\) ,
\( M_{3,3} = Det \begin{bmatrix}
-1&0& .\\
3&2& . \\
. & . & .
\end{bmatrix} = - 2\)
Matrix C of cofactors whose entries defined are defined as
\( C_{i,j} = (-1)^{i+j} M_{i,j} \)
\[ C = \begin{bmatrix}
2&-3&0\\
0&-1&0 \\
- 6 & 11 & -2
\end{bmatrix} \]
We need to find D the determinant of A using the third row (it has 2 zeros!)
\( D = A_{3,3} M_{3,3} = - 2 \)
The inverse of A is given by
\( A^{-1} = \dfrac{1}{D} C^T = -\dfrac{1}{2} \begin{bmatrix} 2&0&-6\\ -3&-1&11\\ 0&0&-2 \end{bmatrix} = \begin{bmatrix} -1&0&3\\ \dfrac{3}{2}& \dfrac{1}{2} & -\dfrac{11}{2}\\ 0&0&1\end{bmatrix}\)
- Solution to Question 3
Given
\( A B = C \)
Right multiply both sides by \( B^{-1} \)
\( A B B^{-1} = C B^{-1}\)
Use associativity on the left side
\( A (B B^{-1}) = C B^{-1} \)
Simplify
\( A I = C B^{-1} \)
\( A = C B^{-1} \)
Use the formula for the inverse of a 2 by 2 matrix to find the inverse of B.
\( Det(B) = -3 \)
\( B^{-1} = - \dfrac{1}{3} \begin{bmatrix}
1&1\\
2& -1
\end{bmatrix} \)
\( A = C B^{-1} = \begin{bmatrix}
2 & -1\\
-2 & 2
\end{bmatrix} (- \dfrac{1}{3}) \begin{bmatrix}
1&1\\
2& -1
\end{bmatrix} = \begin{bmatrix}
0&-1\\
-2/3& 4/3
\end{bmatrix}\)
Note: you may check the answer for matrix A by substituting in the equation \( A B = C \)
- Solution to Question 4
A matrix is invertible if its determinant is not equal to zero.
a) Using the second column,
Det\(
\begin{bmatrix}
k & -1 & 4\\
2 & 0 & 1\\
-1 & 0 & -1
\end{bmatrix} = - 1\)
The matrix is invertible for any k real
b) Det\( \begin{bmatrix}
k & -1 \\
-1 & 3
\end{bmatrix} = 3k - 1\)
\( 3k - 1 \ne 0 \)
\( k \ne 1/3 \)
The matrix in part b) is invertible for all real values of k not equal to 1/3.
c) The given matrix is an upper triangular matrix and its determinant is equal to the product of the terms in the diagonal left to right.
Det \(
\begin{bmatrix}
k & -1 & 4\\
0 & k + 1 & 1\\
0 & 0 & k -3
\end{bmatrix} k(k+1)(k-3)\)
\( k(k+1)(k-3) \ne 0 \)
The given matrix is invertible if k is not equal to 0, - 1 or 3.
- Solution to Question 5
Right multiply the two sides of the equation by \( S^{-1} \)
\( P S^{-1} = Q R^{-1} S S^{-1} \)
simplify
\( P S^{-1} = Q R^{-1} I \)
\( P S^{-1} = Q R^{-1} \)
Left multiply the two sides of the equation by \( Q^{-1} \)
\( Q^{-1} P S^{-1} = Q^{-1} Q R^{-1} \)
simplify
\( Q^{-1} P S^{-1} = I R^{-1}\)
\( Q^{-1} P S^{-1} = R^{-1} \)
Take the inverse of both sides
\( (Q^{-1} P S^{-1})^{-1} = (R^{-1})^{-1} \)
Simplify
\( R = S P^{-1} Q \)
- Solution to Question 6
Write the augmented matrix \( [ A | I ]\)
\( \begin{bmatrix}
a & 0 & 0 & 0&|&1&0&0&0\\
0 & b & 0 & 0&|&0&1&0&0 \\
0 & 0 & c & 0 &|& 0 & 0 & 1 & 0\\
0 & 0 & 0 & d &|& 0 & 0 & 0 & 1
\end{bmatrix} \)
Multiply row (1) by 1/a, row (2) by 1/b, row (3) by 1/c and row (4) by 1/d and simplify
\( \begin{bmatrix}
1 & 0 & 0 & 0&|&1/a&0&0&0\\
0 & 1 & 0 & 0&|&0&1/b&0&0 \\
0 & 0 & 1 & 0 &|& 0 & 0 & 1/c & 0\\
0 & 0 & 0 & 1 &|& 0 & 0 & 0 & 1/d
\end{bmatrix} \)
The inverse of the given matrix is
\( A^{-1} = \begin{bmatrix}
1/a&0&0&0\\
0&1/b&0&0 \\
0 & 0 & 1/c & 0\\
0 & 0 & 0 & 1/d
\end{bmatrix} \)
- Solution to Question 7
The system is of the form
A X = B with A = \(
\begin{bmatrix}
1&0&1&2\\
-1& 1 & 2 & 0 \\
-2& 0 & 1 & 2 \\
0 & 0 & 0 & 1
\end{bmatrix} \) , \( B =\begin{bmatrix}
0\\
1 \\
-1\\
2
\end{bmatrix}
\) and \( X = \begin{bmatrix}
x_1\\
x_2 \\
x_3\\
x_4
\end{bmatrix} \)
Right multiply both sides of the equation by \( A^{-1} \) and simplify.
\( A^{-1} A X = A^{-1} B \)
\( I_3 X = A^{-1} B , I_3 \) is the 3 by 3 identity matrix
Simplify the above
\( X = A^{-1} B \)
The inverse of matrix A was calculated in question 1 and is given by (it is matrix B in question 1)
\( A^{-1} = \begin{bmatrix} 1/3&0&-1/3&0\\
-1&1&-1&4 \\
2/3 & 0 & 1/3 & -2\\
0 & 0 & 0 & 1
\end{bmatrix}
\)
\( \begin{bmatrix}
x_1\\
x_2 \\
x_3\\
x_4
\end{bmatrix} = A^{-1} B = \begin{bmatrix} 1/3&0&-1/3&0\\
-1&1&-1&4 \\
2/3 & 0 & 1/3 & -2\\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
0\\
1 \\
-1\\
2
\end{bmatrix} = \begin{bmatrix}\dfrac{1}{3}\\ 10\\ -\dfrac{13}{3}\\ 2\end{bmatrix}\)
- Solution to Question 8
Since matrix A is common to all the given systems, the most efficient method solving systems of equations of the form
\( A X_1 = B_1 \) , \( A X_2 = B_2 \) , \( A X_3 = B_3 \) ... \( A X_2 = B_i \)
is to find the inverse of matrix A and solve as follows (see question 7 above)
\( X_1 = A^{-1} B_1 \) , \( X_2 = A^{-1} B_2 \) , \( X_3 = A^{-1} B_3 \) ... \( X_i = A^{-1} B_i \)
Solution to Question 9
A and B are invertible matrices of the same dimension related by: \( A^{-1} = A B \).
Find B in terms of A or its inverse.
Right multiply the equation by \( A^{-1} \)
\( A^{-1} A^{-1} = A^{-1} A B \)
simplify
\( A^{-1} A^{-1} = I B \)
simplify to
\( B = A^{-2}\)
- Solution to Question 10
There are many possible answers to both parts of this question.
1)
\(A = \begin{bmatrix} 1 & 1\\
0 & 0 \\
\end{bmatrix} , B = \begin{bmatrix} 0 & 0\\
- 1 & 1 \\
\end{bmatrix} \) ,
\(A + B = \begin{bmatrix} 1 & 1\\
- 1 & 0 \\
\end{bmatrix} \)
2) \(A = \begin{bmatrix} 3 & 1\\
0 & 0 \\
\end{bmatrix} , B = \begin{bmatrix} 0 & 0\\
- 1 & 4 \\
\end{bmatrix} \) ,
\(A - B = \begin{bmatrix} 3 & 1\\
1 & - 4 \\
\end{bmatrix} \)
Check that the determinant of matrices A and B are equal to zero and therefore non invertible. Check that the determinants of A + B and A - B are not equal to zero and therefore invertible.
- Solution to Question 11
Let \(A = \begin{bmatrix} a & b\\
c & d \\
\end{bmatrix} \)
We shall use the method of cofactors. We first calculate the minors
\( M_{1,1} = d\) , \( M_{1,2} = c\) , \( M_{2,1} = b\) , \( M_{2,2} = a\)
Then the cofactors using the formula: \( C_{i,j} = (-1)^{i+j}M_{i,j} \)
\( C_{1,1} = d\) , \( C_{1,2} = - c\) , \( C_{2,1} = - b\) , \( C_{2,2} = a\)
The determinant of A is
\( D = a d - b c \)
\( A^{-1} = \dfrac{1}{a d - b c} \begin{bmatrix} d & - c\\
- d & a \\
\end{bmatrix}^T = \dfrac{1}{a d - b c} \begin{bmatrix} d & - d\\
- c & a \\
\end{bmatrix} \)
- Solution to Question 12
The solutions may be written in matrix form as follows
\( A \begin{bmatrix}
-1 & 0 & 1 \\
2 & - 1 & 1\\
3 & 1 & 1
\end{bmatrix} = \begin{bmatrix}
5 & 4 & 4\\
17 & 2 & 5\\
5 & 2 & 3
\end{bmatrix} \)
which gives
\( A = \begin{bmatrix}
5 & 4 & 4\\
17 & 2 & 5\\
5 & 2 & 3
\end{bmatrix}
\begin{bmatrix}
-1 & 0 & 1 \\
2 & - 1 & 1\\
3 & 1 & 1
\end{bmatrix}^{-1} \)
which gives
\( A^{-1} =
\begin{bmatrix}
-1 & 0 & 1 \\
2 & - 1 & 1\\
3 & 1 & 1
\end{bmatrix}
\begin{bmatrix}
5 & 4 & 4\\
17 & 2 & 5\\
5 & 2 & 3
\end{bmatrix}^{-1}
\)
The solution X is given by
\( X = A^{-1} B = \begin{bmatrix}
-1 & 0 & 1 \\
2 & - 1 & 1\\
3 & 1 & 1
\end{bmatrix}
\begin{bmatrix}
5 & 4 & 4\\
17 & 2 & 5\\
5 & 2 & 3
\end{bmatrix}^{-1} \begin{bmatrix}
1\\
-9 \\
-1
\end{bmatrix} = \begin{bmatrix}
1\\
-2 \\
-1
\end{bmatrix} \)
More References and Links to Matrices