
Examples and questions on matrices along with their solutions are presented .
The following are examples of matrices (plural of matrix).

Example 1
The following matrix has 3 rows and 6 columns.
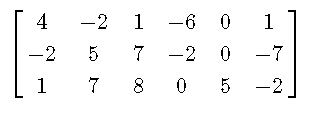
The entry (or element) in a row i and column j of a matrix A (capital letter A) is denoted by the symbol \((A)_{ij} \) or \( a_{ij} \) (small letter a).
In the matrix A shown below, \(a_{11} = 5 \), \(a_{12} = 2 \), etc ... or \( (A)_{11} = 5 \), \( (A)_{12} = 2 \), etc ... \[ \textbf{A} = \begin{bmatrix} 5 & 2 & 7 & -3 \\ -9 & -2 & -7 & 11\\ \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ \end{bmatrix} \]
A square matrix has the number of rows equal to the number of columns.
For each matrix below, determine the order and state whether it is a square matrix.
\[
a) \begin{bmatrix}
-1 & 1 & 0 & 3 \\
4 & -3 & -7 & -9\\
\end{bmatrix}
\;\;\;\;
b) \begin{bmatrix}
-6 & 2 & 0 \\
3 & -3 & 4 \\
-5 & -11 & 9
\end{bmatrix}
\;\;\;\;
\\
c) \begin{bmatrix}
1 & -2 & 5 & -2
\end{bmatrix}
\;\;\;\;
d) \begin{bmatrix}
-2 & 0 \\
0 & -3
\end{bmatrix}
\;\;\;\;
e) \begin{bmatrix}
3
\end{bmatrix}
\]
Solutions
a) order: 2 × 4. Number of rows and columns are not equal therefore not a square matrix.
b) order: 3 × 3. Number of rows and columns are equal therefore this matrix is a square matrix.
c) order: 1 × 4. Number of rows and columns are not equal therefore not a square matrix. A matrix with one row is called a row matrix (or a row vector).
d) order: 2 × 2. Number of rows and columns are equal therefore this is square matrix.
e) order: 1 × 1. Number of rows and columns are equal therefore this matrix is a square matrix.
An identity matrix In is an n×n square matrix with all its element in the diagonal equal to 1 and all other elements equal to zero.
Example 4
The following are all identity matrices.
\[I_1= \begin{bmatrix}
1 \\
\end{bmatrix}
\quad , \quad
I_2= \begin{bmatrix}
1 & 0\\
0& 1
\end{bmatrix} \quad , \quad
I_3= \begin{bmatrix}
1 & 0 & 0\\
0& 1 & 0 \\
0 & 0 & 1
\end{bmatrix} \]
A diagonal matrix is a square matrix with all its elements (entries) equal to zero except the elements in the main diagonal from top left to bottom right. \[A = \begin{bmatrix} 6 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & 2 \end{bmatrix} \]
An upper triangular matrix is a square matrix with all its elements below the main diagonal equal to zero. Matrix U shown below is an example of an upper triangular matrix.
A lower triangular matrix is a square matrix with all its elements above the main diagonal equal to zero. Matrix L shown below is an example of a lower triangular matrix.
\(U = \begin{bmatrix}
6 & 2 & -5 \\
0 & -2 & 7 \\
0 & 0 & 2
\end{bmatrix} \qquad
L = \begin{bmatrix}
6 & 0 & 0 \\
-2 & -2 & 0 \\
10 & 9 & 2
\end{bmatrix} \)
The transpose of an m×n matrix \( A \) is denoted \( A^T \) with order n×m and defined by
\[ (A^T)_{ij} = (A)_{ji} \]
Matrix \( A^T \) is obtained by transposing (exchanging) the rows and columns of matrix \( A \).
Example 5
\[ \begin{bmatrix}
6 & 0 \\
-2 & -2\\
10 & 9
\end{bmatrix} ^T = \begin{bmatrix}
6 & -2 & 10 \\
0 & -2 &9\\
\end{bmatrix} \]
Transpose a matrix an even number of times and you get the original matrix: \( ((A)^T)^T = A \). Transpose matrix an odd number of times and you get the transpose matrix: \( (((A)^T)^T)^T = A^T \).
The transpose of any square diagonal matrix is the matrix itself.
\[ \begin{bmatrix}
3 & 0 & 0 \\
0 & -2 & 0 \\
0 & 0 & 6
\end{bmatrix} ^T = \begin{bmatrix}
3 & 0 & 0 \\
0 & -2 & 0 \\
0 & 0 & 6
\end{bmatrix} \]
A square matrix is symmetric if its elements are such that \( A_{ij} = A_{ji} \) in other words \( A \) is symmetric if \(A = A^T \).
Example 6
Symmetric matrices
\[ \begin{bmatrix}
4 & -2 & 1 \\
-2 & 5 & 7 \\
1 & 7 & 8
\end{bmatrix} \]
Given the matrices:
\[
A = \begin{bmatrix}
-1 & 23 & 10 \\
0 & -2 & -11 \\
\end{bmatrix}
,\quad
B = \begin{bmatrix}
-6 & 2 & 10 \\
3 & -3 & 4 \\
-5 & -11 & 9 \\
1 & -1 & 9
\end{bmatrix}
,\quad
C = \begin{bmatrix}
-3 & 2 & 9 & -5 & 7
\end{bmatrix} \\
D = \begin{bmatrix}
-2 & 6 \\
-5 & 2\\
\end{bmatrix}
,\quad
E = \begin{bmatrix}
3
\end{bmatrix}
,\quad
F = \begin{bmatrix}
3 \\
5 \\
-11 \\
7
\end{bmatrix}
,\quad
G = \begin{bmatrix}
-6 & -4 & 23 \\
-4 & -3 & 4 \\
23 & 4 & 9 \\
\end{bmatrix}
\]
a) What is the dimension of each matrix?
b) Which matrices are square?
c) Which matrices are symmetric?
d) Which matrix has the entry at row 3 and column 2 equal to -11?
e) Which matrices has the entry at row 1 and column 3 equal to 10?
f) Which are column matrices?
g) Which are row matrices?
h) Find \( A^T , C^T , E^T , G^T \).
1) Given the matrices:
\[
A = \begin{bmatrix}
23 & 10 \\
0 & -11 \\
\end{bmatrix}
,\quad
B = \begin{bmatrix}
-6 & 0 & 0 \\
-1 & -3 & 0 \\
-5 & 3 & -9 \\
\end{bmatrix}
,\quad
C = \begin{bmatrix}
-3 & 0\\
0 & 2
\end{bmatrix} \\
,\quad
D = \begin{bmatrix}
-7 & 3 & 2 \\
0 & 2 & 4 \\
0 & 0 & 9 \\
\end{bmatrix}
,\quad
E = \begin{bmatrix}
12 & 0 & 0 \\
0 & 23 & 0 \\
0 & 0 & -19\\
\end{bmatrix}
\]
a) Which of the above matrices are diagonal?
b) Which of the above matrices are lower triangular?
c) Which of the above matrices are upper triangular?
a) A: 2 × 3, B: 4 × 3, C: 1 × 5, D: 2 × 2, E: 1 × 1, F: 4 × 1, G: 3 × 3,
b) D, E and G
c) E and G
d) B
e) A and B
f) E and F
g) E and C
h)
\[
A^T = \begin{bmatrix}
-1 & 0 \\
23 & -2 \\
10 & -11
\end{bmatrix}
,\quad
C^T = \begin{bmatrix}
-3 \\
2\\
9\\-5\\7
\end{bmatrix}
,\quad
E^T = \begin{bmatrix}
3
\end{bmatrix}
,\quad
G^T = \begin{bmatrix}
-6 & -4 & 23\\
-4 & -3 & 4\\
23 & 4 & 9
\end{bmatrix}
\]