Null Space and Nullity of a Matrix
Definition of Null Space of a Matrix
The null space of an m × n matrix A is the set of all the solutions x to the homogeneous equation
A x = 0
where x is a column vector with n rows and 0 is a zero column vector with n rows.
The null space of matrix A is denoted as "Null A" .
Null A is a subspace of ℝ n and vectors x are in ℝ n .
Using set notation we write: 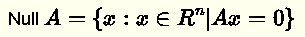
The nullity of matrix A is the dimension of Null A which equal to the number of vectors in Null A .
Properties of the Null Space
Let A be an m × n matrix.
- The null space of a given matrix A is never empty since x = 0 is a trivial solution to the homogeneous equation A x = 0 .
- Null A is a subspace of ℝ n
-
All elements of Null A are vectors in ℝ n.
Examples with Solutions
Example 1
Which of the vectors
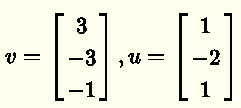 is an element of Null A given that
is an element of Null A given that
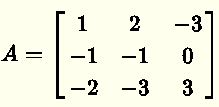
Solution to Example 1
From the above definition, any element of Null A must be a solution to the homogeneous equation A x = 0 . Therefore,
in order to find out if a given vector is an elelment of Null A , we just check whether it is a solution to the homogeneous equation.
Check vector v
Evaluate the product A v
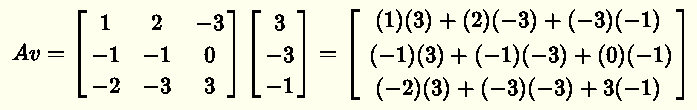 \( \)\( \)\( \)
\( \)\( \)\( \)
Simplify
\( = \begin{bmatrix}
0\\\
0 \\
0
\end{bmatrix}
\)
Hence since \( \; A v \; \) is equal to \( 0 \), vector \( v = \begin{bmatrix}
3\\
-3\\
-1
\end{bmatrix} \) is a solution to the homogeneous equation \( A x = 0 \) and is therefore an element of Null \( A \).
Check vector \( u \)
Evaluate the product \( A u \)
\( \begin{bmatrix}
1 & 2 & -3\\
-1 & -1 & 0\\
-2 & -3 & 3
\end{bmatrix}
\begin{bmatrix}
1\\
-2\\
1
\end{bmatrix}
=
\begin{bmatrix}
(1)(1) + (2)(-2) + (-3)(1)\\\
(-1)(1) + (-1)(-2) + (0)(1) \\
(-2)(1) + (-3)(-2) + 3(1)
\end{bmatrix}
\)
Simplify
\( = \begin{bmatrix}
-4\\\
1\\
7
\end{bmatrix}
\)
Hence since the \( \; A u \;\) is NOT equal to \( 0 \), vector \( u = \begin{bmatrix}
1\\
-2\\
1
\end{bmatrix} \) is a NOT solution to the homogeneous equation \( A x = 0 \) and therefore is NOT an element of Null \( A \).
Example 2
a) Find Null A given that \( A = \begin{bmatrix}
1 & 2 \\
0 & 0
\end{bmatrix} \)
b) Find 3 elements that are in Null A.
Solution to Example 2
a)
To find the Null A, we need to solve the equation \( A x = 0 \) where \( x \) is a vector in \( \mathbb{R}^2 \)
Let \( x = \begin{bmatrix}
x_1\\
x_2
\end{bmatrix} \)
We need to solve
\( \begin{bmatrix}
1 & 2 \\
0 & 0
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}
= \begin{bmatrix}
0\\
0
\end{bmatrix}
\)
Write the augmented matrix of the equation \( A x = 0 \)
\( \begin{bmatrix}
1 & 2 & | & 0\\
0 & 0 & | & 0
\end{bmatrix} \)
Solve the above. \( x_2 \) is a free variable and
\( x_1 = - 2 x_2 \)
Hence the solution set may be written of the form
\( x = x_2 \begin{bmatrix}
-2\\
1
\end{bmatrix} \) , where \( x_2 \in \mathbb{R} \)
Any real value of \( x_3 \) gives an element in Null \( A \).
Hence Null \(A\) is the subspace spanned by \( \begin{bmatrix}
-2 \\
1
\end{bmatrix} \)
b)
Note that for \( x_2 = 0 \), we have the trivial solution \( x = 0 \begin{bmatrix}
-2\\
1
\end{bmatrix} =
\begin{bmatrix}
0\\
0
\end{bmatrix}
\)
More elements of Null \( A \) may be obtained by setting the free variable \( x_2 \) to different values.
Let \( x_2 = -1\), hence the corresponding element of Null \( A \): \( x = -1 \begin{bmatrix}
-2\\
1
\end{bmatrix} =
\begin{bmatrix}
2\\
-1
\end{bmatrix}
\)
Let \( x_2 = 2\), hence the corresponding element of Null \( A \): \( x = 2 \begin{bmatrix}
-2\\
1
\end{bmatrix} =
\begin{bmatrix}
-4\\
2
\end{bmatrix}
\)
Let \( x_2 = \dfrac{1}{2} \), hence the corresponding element of Null \( A \): \( x = \dfrac{1}{2} \begin{bmatrix}
-2\\
1
\end{bmatrix} =
\begin{bmatrix}
-1\\
\dfrac{1}{2}
\end{bmatrix}
\)
As an exercise, check that the three elements \( \begin{bmatrix}
2\\
-1
\end{bmatrix} , \begin{bmatrix}
-4\\
2
\end{bmatrix}
,
\begin{bmatrix}
-1\\
\dfrac{1}{2}
\end{bmatrix} \) obtained above are solutions to the equation \( A x = 0 \).
Example 3
a) Find Null A and the nullity of \( A \) given that \( A = \begin{bmatrix}
1 & 2 & -1 \\
1 & -1 & 1 \\
3 & 0 & 1
\end{bmatrix} \)
Solution to Example 3
Let \( x = \begin{bmatrix}
x_1 \\
x_2\\
x_3
\end{bmatrix} \) be the solution of \( A x = 0 \)
We need to solve the system
\( \begin{bmatrix}
1 & 2 & -1 \\
1 & -1 & 1 \\
3 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2\\
x_3
\end{bmatrix}
= \begin{bmatrix}
0\\
0\\
0
\end{bmatrix}
\)
Write the augmented matrix of the above equation.
\(
\begin{bmatrix}
1 & 2 & -1 & | & 0\\
1 & -1 & 1 & | & 0\\
3 & 0 & 1 & | & 0
\end{bmatrix}
\)
Row reduce using Gauss Jordan method
\(
\begin{bmatrix}
1 & 0 & \dfrac{1}{3} & | & 0\\
0 & 1 & -\dfrac{2}{3} & | & 0\\
0 & 0 & 0 & | & 0
\end{bmatrix}
\)
\( x_3 \) is the free variable.
\( x_2 = \dfrac{2}{3} x_3 \)
\( x_1 = -\dfrac{1}{3} x_3 \)
The solution \( x \) may be written as
\( x = x_3 \begin{bmatrix}
-\dfrac{1}{3} \\
\dfrac{2}{3} \\
1
\end{bmatrix} \)
Hence Null \(A\) is the subspace spanned by \( \begin{bmatrix}
-\dfrac{1}{3} \\
\dfrac{2}{3} \\
1
\end{bmatrix} \)
Nullity of \( A \) = the number of vector in Null \(A\) = 1
Example 4
a) Find Null A and the nullity of \( A \) given that \( A = \begin{bmatrix}
3 & -2 & -1 & 0 & 2\\
1 & -2 & 1 & -2 & 4\\
-4 & 4 & 0 & 2 & -6
\end{bmatrix} \)
Solution to Example 4
The system to solve is
\( A x = 0 \)
which may be written as
\( \begin{bmatrix}
3 & -2 & -1 & 0 & 2\\
1 & -2 & 1 & -2 & 4\\
-4 & 4 & 0 & 2 & -6
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2\\
x_3\\
x_4\\
x_5
\end{bmatrix}
= \begin{bmatrix}
0\\
0\\
0
\end{bmatrix}
\)
We first write the augmented matrix of the above system
\(
\begin{bmatrix}
3 & -2 & -1 & 0 & 2 & | & 0\\
1 & -2 & 1 & -2 & 4 & | & 0\\
-4 & 4 & 0 & 2 & -6 & | & 0
\end{bmatrix}
\)
We row reduce the above matrix
\(
\begin{bmatrix}
1 & 0 & -1 & 1 & -1 & | & 0\\
0 & 1 & -1 & \dfrac{3}{2} & -\dfrac{5}{2} & | & 0 \\
0 & 0 & 0 & 0 & 0 & | & 0
\end{bmatrix}
\)
Solve the system corresponding to the augmented matrix
The free variables are: \( x_3, \;x_4, \;x_5 \), hence
The second row gives: \( x_2 = x_3 - \dfrac{3}{2} x_4 + \dfrac{5}{2} x_5 \)
The first row gives: \( x_1 = x_3 - x_4 + x_5 \)
The solution vector \( x \) is given by
\( x = \begin{bmatrix}
x_3 - x_4 + x_5 \\
x_3 - \dfrac{3}{2} x_4 + \dfrac{5}{2} x_5 \\
x_3 \\
x_4 \\
x_5
\end{bmatrix}
\)
which may be written as
\( x = x_3 \begin{bmatrix}
1\\
1\\
1\\
0 \\
0
\end{bmatrix}
+
x_4 \begin{bmatrix}
- 1\\
- \dfrac{3}{2}\\
0 \\
1\\
0
\end{bmatrix}
+
x_5 \begin{bmatrix}
1\\
\dfrac{5}{2} \\
0 \\
0 \\
1
\end{bmatrix}
\)
Null A = Span \( \left\{ \begin{bmatrix}
1\\
1\\
1\\
0\\
0
\end{bmatrix}
,
\begin{bmatrix}
-1\\
-\dfrac{3}{2}\\
0\\
1\\
0
\end{bmatrix}
,
\begin{bmatrix}
1\\
\dfrac{5}{2}\\
0\\
0\\
1
\end{bmatrix}
\right\}
\)
Nullity of \( A \) is equal to the number of vectors in the basis of Null \( A \) = 3.
As an exercise, select any real values for \( x_3, \; x_4\) and \( x_5 \), calculate vector \( x = x_3 \begin{bmatrix}
1\\
1\\
1\\
0 \\
0
\end{bmatrix}
+
x_4 \begin{bmatrix}
- 1\\
- \dfrac{3}{2}\\
0 \\
1\\
0
\end{bmatrix}
+
x_5 \begin{bmatrix}
1\\
\dfrac{5}{2} \\
0 \\
0 \\
1
\end{bmatrix}
\) and verify that it is a solution to the system \( A x = 0 \).
More References and links
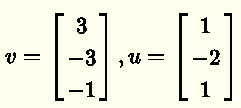 is an element of Null A given that
is an element of Null A given that
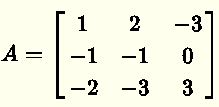
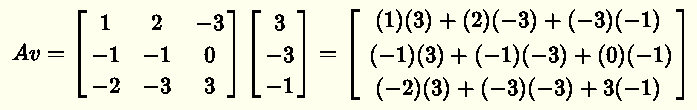 \( \)\( \)\( \)
\( \)\( \)\( \)