Pivots of a Matrix in Row Echelon Form - Examples with Solutions

Definition of a Matrix in Row Echelon Form and Pivots

A matrix is in row echelon form if it has the following properties.
  1. All rows (of the matrix) with zeros only are located at the bottom of the matrix.
  2. Any row that does not contain only zeros its first non zero number is a 1 also is called the leading 1. These are also called pivots.
  3. For two successive rows with leading 1's, the 1 in the lower row is to the right of the 1 in the upper row.
A row echelon form calculator is included.
Definition For a matrix is in row echelon form, the pivot points (position) are the leading 1's in each row and are in red in the examples below.
Examples of matrices in row echelon form
Matrix in Row Echelon Form
The pivots are: the leading 1 in row 1 column 1, the leading 1 in row 2 column 2 and the leading 1 in row 3 column 3. (red color)

Matrix in Row Echelon Form

The pivots are: the leading 1 in row 1 column 1, the leading 1 in row 2 column 3 and the leading 1 in row 3 column 5. (red color)

Questions with Solution

For the following matrices; which ones are NOT in row echelon form? Explain why.
For those who are in row echelon form, give the position of the pivots.
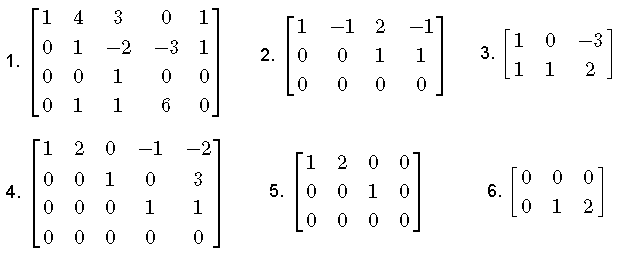
Matrices NOT in Row Echelon Form

Solutions to the Above Questions


  1. Matrix 1 is not in row echelon form because the leading 1 in row 4 is not to the right of the leading 1 in row 3 (see condition 3 in the above definition of matrices in row echelon form).
  2. Matrix 2 is in row echelon form. 2 Pivots; one at row 1 column 1 and one at row 2 column 3
  3. Matrix 3 is not in row echelon form because the leading 1 in row 2 is not to the right of the leading 1 in row 1 (see condition 3 in the above definition of matrices in row echelon form).
  4. Matrix 4 is in row echelon form. 3 Pivots; one at row 1 column 1, one at row 2 column 3 and one at row 3 column 4
  5. Matrix 5 is in row echelon form. 2 Pivots; one at row 1 column 1 and one at row 2 column 3
  6. Matrix 6 is not in row echelon form. Row 1 with zeros only must be located at the bottom of the matrix (see condition 1 in the above definition of matrices in row echelon form).


More References and links

  1. linear algebra
  2. Solve a system of linear equations by elimination
  3. inverse of a matrix
  4. elementary matrices
  5. Reduced Row echelon form
  6. Gaussian Elimination