Row Operations and Elementary Matrices
We show that when we perform elementary row operations on systems of equations represented by
 it is equivalent to multiplying both sides of the equations by an elementary matrix to be defined below.
it is equivalent to multiplying both sides of the equations by an elementary matrix to be defined below.
We consider three row operations involving one single elementary operation at the time. We start with examples and detailed solutions and end up with questions and their solutions.
Elementary Matrix Equivalent to Interchanging two Rows of a Matrix
We start with the given system in matrix form
.gif) Interchange rows (1) and (3) and rewrite the system as
Interchange rows (1) and (3) and rewrite the system as
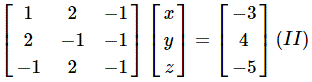 Let us now consider the identity matrix
Let us now consider the identity matrix

We interchange row (1) and (3) in 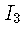 to obtain the elementary matrix
to obtain the elementary matrix  given by
given by
 and multiply both sides of system (I) by
and multiply both sides of system (I) by  as follows
as follows

Multiply the matrices, using the associativity on the left side, and simplify to

which is the system of equations (II) obtained above by interchanging rows (1) and (3) in the system (I).
Conclusion : Interchanging rows (1) and (3) is equivalent to multiplying (from the left) the two sides of the system by the elementary matrix
 obtained from the identity matrix
obtained from the identity matrix 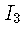 .
.
Elementary Matrix Equivalent to Multiplying a Row by a Constant in a Matrix
Let us now consider the system of equations (II) and multiply row (3) by 2 to obtain
\( \)\( \) \( \)
\[ \begin{bmatrix} 1 & 2 & -1 \\ 2 & -1 & -1 \\ -2 & 4 & - 2 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} -3 \\ 4 \\ -10 \end{bmatrix} (III) \]
Take \( I_3 \) multiply its third row by 2 to obtain the elementary matrix \( E_2 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \) and multiply both sides of the system (II) by \( E_2 \) as follows:
\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} 1 & 2 & -1 \\ 2 & -1 & -1 \\ -1 & 2 & - 1 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} -3 \\ 4 \\ -5 \end{bmatrix} \]
Use associativity, multiply and simplify the above to obtain
\[ \begin{bmatrix} 1 & 2 & -1 \\ 2 & -1 & -1 \\ -2 & 4 & - 2 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} -3 \\ 4 \\ -10 \end{bmatrix} \]
which is exactly the system of equations (III).
Conclusion: Multiplying row (3) by 2 is equivalent to multiplying the two sides of the system by the elementary matrix \( E_2 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix}\) obtained from the identity matrix \( I_3 \).
Elementary Matrix Equivalent to Adding a Multiple of a Row to Another Row in a Matrix
Let us now consider the system of equations (III), multiply row (1) by - 2 add it to row (2) to obtain:
\[ \begin{bmatrix} 1 & 2 & -1 \\ 0 & - 5 & 1 \\ -2 & 4 & - 2 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} -3 \\ 10 \\ -10 \end{bmatrix} (IV) \]
Take \( I_3 \) multiply its row (1) by - 2 and add it to row (2) to obtain \( E_3 = \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \) and multiply both sides of the system (III) by \( E_3 \) as follows:
\[ \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & -1 \\ 2 & -1 & -1 \\ -2 & 4 & - 2 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} -3 \\ 4 \\ -10 \end{bmatrix} \]
Use associativity, multiply and simplify the above to obtain
\[ \begin{bmatrix} 1 & 2 & -1 \\ 0 & - 5 & 1 \\ -2 & 4 & - 2 \end{bmatrix}
\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} -3 \\ 10 \\ -10 \end{bmatrix} \]
which exactly the system of equations (IV).
Conclusion: Add row (1) multiplied by - 2 to row (2) is equivalent to multiplying the two sides of the system by the elementary matrix \( E_3 = \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\) obtained from the identity matrix \( I_3 \).
Inverse of the Elementary Matrices
One of the advantages in using elementary matrices is that their inverse can be obtained without heavy calculations.
Inverse of Elementary Matrix E1
In the above examples, We obtained the elementary matrix \( E_1 \) by interchanging rows (1) and (3), the inverse of \( E_1 \) is obtained from I3 by interchanging rows (3) and (1); hence the inverse of \( E_1 \) is given by
\[ E_1^{-1} = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix} \]
We now check that
\( E_1 \cdot E_1^{-1} = E_1^{-1} \cdot E_1^ = I_3 \)
\[ E_1 \cdot E_1^{-1} = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]
There no need to check that \( E_1^{-1} \cdot E_1^ = I_3 \) beacuse \( E_1 = E_1^{-1} \).
Inverse of Elementary Matrix E2
In the above examples, We obtained the elementary matrix \( E_2 \) by multiplying row (3) by 2, the inverse of \( E_2 \) is obtained from I3 by dividing row (3) by 2; hence the inverse of \( E_2 \) is given by
\[ E_2^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1/2 \end{bmatrix} \]
We now check that
\( E_2 \cdot E_2^{-1} = E_2^{-1} \cdot E_2^ = I_3 \)
\[ E_2 \cdot E_2^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1/2 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]
\[ E_2^{-1} \cdot E_2^ = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1/2 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]
Inverse of Elementary Matrix E3
In the above examples, We obtained the elementary matrix \( E_3 \) by multiply row (1) by - 2 add it to row (2). The inverse of \( E_3 \) is obtained from I3 by multiplying row (1) by - 2 and subtracting it from row (2); hence the inverse of \( E_3 \) is given by
\[ E_3^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
We now check that
\( E_3 \cdot E_3^{-1} = E_3^{-1} \cdot E_3^ = I_3 \)
\[ E_3 \cdot E_3^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]
\[ E_3^{-1} \cdot E_3^ = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]
Questions on Elementary Matrices
- Part 1
Which of the following is an elementary? Explain.
\[
A = \begin{bmatrix}
0 & 1 \\
1 & 0\\
\end{bmatrix}
,\quad
B = \begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0 \\
\end{bmatrix}
,\quad
C = \begin{bmatrix}
1 & 0\\
4 & 1
\end{bmatrix} \\
,\quad
D = \begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
-5 & 0 & 1 \\
\end{bmatrix}
,\quad
E = \begin{bmatrix}
1 & 0 & 0 \\
1 & 1 & 0 \\
1 & 0 & 1 \\
\end{bmatrix}
,\quad
F = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0\\
7 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix}
\]
- Part 2
What is the elementary matrix of the systems of the form \[ A X = B \] for following row operations?
A) A is 2 by 2 matrix, add 3 times row(1) to row(2)?
B) A is 3 by 3 matrix, multiply row(3) by - 6.
C) A is 5 by 5 matrix, multiply row(2) by 10 and add it to row 3.
- Part 3
Find the inverse to each elementary matrix found in part 2.
Solutions
- Part 1
A : interchange rows (1) and (2)
B: interchange rows (2) and (3)
C: add 4 times row (1) to row (2)
D: add - 5 times row (1) to row (3)
E: is not an elementary matrix
F: add 7 times row(1) to row (3)
- Part 2
A)
\(
A = \begin{bmatrix}
1 & 0 \\
3 & 1\\
\end{bmatrix} \)
B)
\(
A = \begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & -6
\end{bmatrix} \)
C)
\(
A = \begin{bmatrix}
1 & 0 & 0 & 0 & 0\\
0 & 1 & 0 &0 & 0 \\
0 & 10 & 1 &0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1
\end{bmatrix} \)
- Part 3
The inverse of the elementary matrices in part 2.
A) Mulriply row(1) by - 3 times and add it to row(3)
\(
A^{-1} = \begin{bmatrix}
1 & 0 \\
-3 & 1\\
\end{bmatrix} \)
B) Divide row (3) by - 6
\(
A^{-1} = \begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & -1/6
\end{bmatrix} \)
C) multiply row(2) by - 10 and add it to row(3).
\(
A^{-1} = \begin{bmatrix}
1 & 0 & 0 & 0 & 0\\
0 & 1 & 0 &0 & 0 \\
0 & -10 & 1 &0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1
\end{bmatrix} \)
More References and links
.gif) Interchange rows (1) and (3) and rewrite the system as
Interchange rows (1) and (3) and rewrite the system as
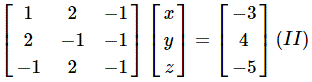 Let us now consider the identity matrix
Let us now consider the identity matrix

![]() to obtain the elementary matrix
to obtain the elementary matrix ![]() given by
given by
 and multiply both sides of system (I) by
and multiply both sides of system (I) by ![]() as follows
as follows


 obtained from the identity matrix
obtained from the identity matrix ![]() .
.