Given a basis
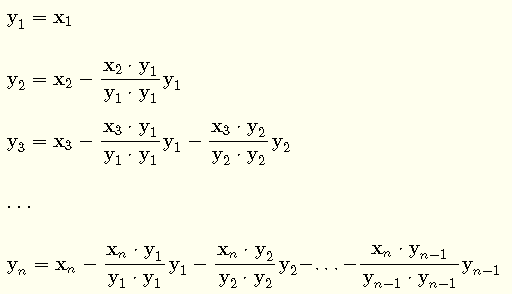
is an orthogonal basis for the subspace V .
The orthonormal basis Y0 is obtained by dividing each vector in the basis Y by its norm.
The Gram Schmidt process is used to produce an Orthonormal Basis for a subspace.
Given a basis
![]() for subspace V ,
the basis
for subspace V ,
the basis
![]() where
where
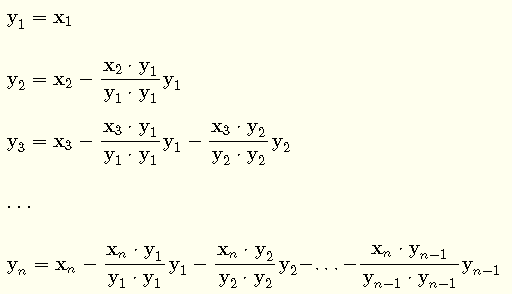
is an orthogonal basis for the subspace V .
![]()
The orthonormal basis Y0 is obtained by dividing each vector in the basis Y by its norm.
Example 1
Subspace \( V \) is defined by span\( \{\textbf{v}_1 , \textbf{v}_2 \} \) where \( \textbf{v}_1 \) and \(\textbf{v}_2 \) are column vectors given by
\( \textbf{v}_1 =
\begin{bmatrix}
1\\
2 \\
0
\end{bmatrix}
\) and \( \textbf{v}_2 =
\begin{bmatrix}
-2 \\
-4 \\
-4
\end{bmatrix}
\)
Use the Gram Schmidt process defined above to determine an orthonormal basis \( Y_O \) for \( V \)
Solution to Example 1
Let \( Y = \{ \textbf{y}_1 , \textbf{y}_2 \} \) be the orthogonal basis to determine. According to the fomrmulas above, we write
\( \textbf {y}_1 = \textbf {v}_1 = \begin{bmatrix}
1\\
2 \\
0
\end{bmatrix}
\)
\( \textbf {y}_2 = \textbf {v}_2 - \dfrac{\textbf {v}_2 \cdot \textbf {y}_1}{\textbf {y}_1 \cdot \textbf {y}_1} \textbf {y}_1 \)
Evaluate the inner product in the numerator and denominator
\( \dfrac{\textbf {v}_2 \cdot \textbf {y}_1}{\textbf {y}_1 \cdot \textbf {y}_1} = \dfrac{\begin{bmatrix}
-2 \\
-4 \\
-4
\end{bmatrix} \cdot \begin{bmatrix}
1\\
2 \\
0
\end{bmatrix} }{ \begin{bmatrix}
1\\
2 \\
0
\end{bmatrix} \cdot \begin{bmatrix}
1\\
2 \\
0
\end{bmatrix} } = \dfrac{-10}{5} = -2\)
Substitute the above and evaluate \( \textbf {y}_2 \)
\( \textbf {y}_2 = \begin{bmatrix}
-2 \\
-4 \\
-4
\end{bmatrix}
- (-2)
\begin{bmatrix}
1\\
2 \\
0
\end{bmatrix}
= \begin{bmatrix}
0\\
0 \\
-4
\end{bmatrix}
\)
Hence \( Y = \left \{\begin{bmatrix}
1\\
2 \\
0
\end{bmatrix}
,
\begin{bmatrix}
0\\
0 \\
-4
\end{bmatrix} \right \} \)
The orthonormal basis \( Y_O \) is obtained by dividing each vector in the basis \( Y \) by its norm.
\( Y_O = \left \{ \dfrac{1}{\sqrt 3}\begin{bmatrix}
1\\
2 \\
0
\end{bmatrix}
,
\dfrac{1}{4} \begin{bmatrix}
0\\
0 \\
-4
\end{bmatrix} \right \} \)
Note that
1) \( Y = \{ \textbf {y}_1 , \textbf {y}_2 \} \) is a basis for \( V \) because it is a linear combination of \( \textbf {v}_1 \) and \( \textbf {v}_2 \).
We know that \( y_1 = v_1 \) and it can easily be shown that \( y_2 = 2 v_1 + v_2 \)
Hence span \( \{ \textbf {v}_1, \textbf{v}_2 \} \) = span \( \{ \textbf {y}_1, \textbf{y}_2 \} \)
2) the inner product of \( \textbf {y}_1 \) and \( \textbf {y}_2 \) given by
\(
\begin{bmatrix}
1\\
2 \\
0
\end{bmatrix}
\cdot
\begin{bmatrix}
0\\
0 \\
-4
\end{bmatrix}
= 0
\)
means that \( \textbf {y}_1 \) and \( \textbf {y}_2 \) are orthogonal and hence \( Y \) is an orthogonal basis for \( V \)
Example 2
Subspace \( V \) is defined by span\( \{\textbf{v}_1 , \textbf{v}_2 , \textbf{v}_3 , \textbf{v}_4\} \) where
\( \textbf{v}_1 =
\begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix}
\) , \( \textbf{v}_2 =
\begin{bmatrix}
1 \\
1 \\
1\\
1\\
0
\end{bmatrix}
\) ,
\( \textbf{v}_3 =
\begin{bmatrix}
0 \\
0 \\
-1\\
-1\\
0
\end{bmatrix}
\)
,
\( \textbf{v}_4 =
\begin{bmatrix}
0 \\
0 \\
0\\
1\\
1
\end{bmatrix}
\)
Use the Gram Schmidt process defined above to determine an orthonormal basis \( Y_O \) for \( V \)
Solution to Example 2
Let \( Y = \{\textbf{y}_1,\textbf{y}_2,\textbf{y}_3,\textbf{y}_4\} \) be the orthogonal basis to determine. Using the fomrmulas above, we write
\( \textbf {y}_1 = \textbf {v}_1 =
\begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix}
\)
\( \textbf {y}_2 = \textbf {v}_2 - \dfrac{\textbf {v}_2 \cdot \textbf {y}_1}{\textbf {y}_1 \cdot \textbf {y}_1} \textbf {y}_1 \)
Evaluate the inner product in the numerator and denominator
\( \dfrac{\textbf {v}_2 \cdot \textbf {y}_1}{\textbf {y}_1 \cdot \textbf {y}_1} = \dfrac{\begin{bmatrix}
1 \\
1 \\
1\\
1\\
0
\end{bmatrix} \cdot \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} }{ \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} \cdot \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} } = \dfrac{2}{19} \)
Substitute the above and evaluate \( \textbf {y}_2 \)
\( \textbf {y}_2 = \begin{bmatrix}
1 \\
1 \\
1\\
1\\
0
\end{bmatrix}
- \dfrac{2}{19}
\begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix}
=
\begin{bmatrix}
\frac{21}{19}\\
\frac{21}{19}\\
\frac{15}{19}\\
\frac{15}{19}\\
-\frac{6}{19}\end{bmatrix}
\)
Note that if we mutliply \( \textbf{y}_2 \) by any number not equal to zero, it would not change the basis. Hence multiply \( \textbf{y}_2 \) by \( \dfrac{19}{3} \) and simplify to
\( \textbf{y'}_2 = \dfrac{19}{3} \begin{bmatrix}
\frac{21}{19}\\
\frac{21}{19}\\
\frac{15}{19}\\
\frac{15}{19}\\
-\frac{6}{19}\end{bmatrix} =
\begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix}
\)
We now use vector \( \textbf {y'}_2 \) instead of \( \textbf {y}_2 \) in the formulas for \( \textbf {y}_3 \).
\( \textbf {y}_3 = \textbf {v}_3 - \dfrac{\textbf {v}_3 \cdot \textbf {y}_1}{\textbf {y}_1 \cdot \textbf {y}_1} \textbf {y}_1
- \dfrac{\textbf {v}_3 \cdot \textbf {y'}_2}{\textbf {y'}_2 \cdot \textbf {y'}_2} \textbf {y'}_2 \)
Substitute
\( \textbf {y}_3 = \begin{bmatrix}
0 \\
0 \\
-1\\
-1\\
0
\end{bmatrix} -
\dfrac{\begin{bmatrix}
0 \\
0 \\
-1\\
-1\\
0
\end{bmatrix} \cdot \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} }{\begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} \cdot \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} } \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix}
\)
\(
- \dfrac{\begin{bmatrix}
0 \\
0 \\
-1\\
-1\\
0
\end{bmatrix} \cdot \begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix} }{\begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix} \cdot \begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix} } \begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix} =
\begin{pmatrix}\frac{1}{4}\\ \frac{1}{4}\\ -\frac{1}{4}\\ -\frac{1}{4}\\ \frac{1}{2}\end{pmatrix}
\)
Multiply \( \textbf {y}_3 \) by 4 to replace it by a vector without fractions.
\( \textbf {y'}_3 = 4 \textbf {y}_3 = \begin{bmatrix}
1\\
1 \\
-1 \\
-1\\
2
\end{bmatrix}\)
Use \( \textbf {y'}_3 \) instead of \( \textbf {y}_3 \) in the formulas
\( \textbf {y}_4 = \textbf {v}_4 - \dfrac{\textbf {v}_4 \cdot \textbf {y}_1}{\textbf {y}_1 \cdot \textbf {y}_1} \textbf {y}_1
- \dfrac{\textbf {v}_4 \cdot \textbf {y'}_2}{\textbf {y'}_2 \cdot \textbf {y'}_2} \textbf {y'}_2
- \dfrac{\textbf {v}_4\cdot \textbf {y'}_3}{\textbf {y'}_3 \cdot \textbf {y'}_3} \textbf {y'}_3 \)
Substitute
\( \textbf {y}_4 = \begin{bmatrix}
0 \\
0 \\
0\\
1\\
1
\end{bmatrix} - \dfrac{\begin{bmatrix}
0 \\
0 \\
0\\
1\\
1
\end{bmatrix} \cdot \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix}}{\begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} \cdot \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix}} \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix}
\)
-
\(
\dfrac{\begin{bmatrix}
0 \\
0 \\
0\\
1\\
1
\end{bmatrix} \cdot \begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix}}{\begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix} \cdot \begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix}} \begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix}
\\ \quad \quad
- \dfrac{\begin{bmatrix}
0 \\
0 \\
0\\
1\\
1
\end{bmatrix} \cdot \begin{bmatrix}
1\\
1 \\
-1 \\
-1\\
2
\end{bmatrix}}{\begin{bmatrix}
1\\
1 \\
-1 \\
-1\\
2
\end{bmatrix} \cdot \begin{bmatrix}
1\\
1 \\
-1 \\
-1\\
2
\end{bmatrix}} \begin{bmatrix}
1\\
1 \\
-1 \\
-1\\
2
\end{bmatrix} = \begin{pmatrix}0\\ 0\\ -\frac{1}{2}\\ \frac{1}{2}\\ 0\end{pmatrix}\)
Multiply \( \textbf {y}_4 \) by 2 to obtain
\( \textbf {y'}_4 = 2 \textbf {y}_4 = \begin{bmatrix}
0\\
0\\
-1 \\
1\\
0
\end{bmatrix}\)
Hence an orthogonal basis for the subset \( V \) may be written as
\( Y = \left \{ \textbf {y}_1 , \textbf {y'}_2 , \textbf {y'}_3 , \textbf {y'}_4 \right \} = \left \{ \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} ,
\begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix}
,
\begin{bmatrix}
1\\
1 \\
-1 \\
-1\\
2
\end{bmatrix}
,
\begin{bmatrix}
0\\
0\\
-1 \\
1\\
0
\end{bmatrix}
\right \} \)
The orthonormal basis \( Y_O \) is obtained by dividing each vector in the basis \( Y \) by its norm.
\( Y_O = \left \{ \dfrac{1}{\sqrt {19}} \begin{bmatrix}
-1\\
-1 \\
2 \\
2\\
3
\end{bmatrix} ,
\dfrac{1}{2\sqrt{38}}
\begin{bmatrix}
7\\
7\\
5\\
5\\
-2
\end{bmatrix}
,
\dfrac{1}{2\sqrt{2}}
\begin{bmatrix}
1\\
1 \\
-1 \\
-1\\
2
\end{bmatrix}
,
\dfrac{1}{\sqrt{2}}
\begin{bmatrix}
0\\
0\\
-1 \\
1\\
0
\end{bmatrix}
\right \} \)
To check that the basis \( Y \) obtained span that same subspace as the given basis \( V \), we row reduce the matrix
\(
\begin{bmatrix}
V | Y
\end{bmatrix}
=
\begin{bmatrix}-1&1&0&0&-1&7&1&0\\ \:\:\:-1&1&0&0&-1&7&1&0\\ \:\:\:2&1&-1&0&2&5&-1&-1\\ \:\:\:2&1&-1&1&2&5&-1&1\\ \:\:\:3&0&0&1&3&-1&2&0\end{bmatrix}
\)
to obtain
\(
\begin{bmatrix}1&0&0&0&1&-\frac{1}{3}&\frac{2}{3}&-\frac{2}{3}\\ 0&1&0&0&0&\frac{20}{3}&\frac{5}{3}&-\frac{2}{3}\\ 0&0&1&0&0&1&4&-1\\ 0&0&0&1&0&0&0&2\\ 0&0&0&0&0&0&0&0\end{bmatrix}
\)
and conlude from the above that
\( y_1 = v_1 \)
\( y_2 = - \dfrac {1}{3} v_1 + \dfrac{20}{3} v_2 + v_3\)
\( y_3 = \dfrac {2}{3} v_1 + \dfrac{5}{3} v_2 + 4 v_3\)
\( y_4 = - \dfrac {2}{3} v_1 - \dfrac{2}{3} v_2 - v_3 + 2 v_4\)
The above results show that span \( \{ \textbf {v}_1, \textbf{v}_2,\textbf{v}_3 ,\textbf{v}_4 \} \) = span \( \{ \textbf {y}_1, \textbf{y}_2, \textbf{y}_3 , \textbf{y}_3 \} \)
Using the inner product, it can easily be shown that \( Y \) is an orthogonal basis.