Linearly Independent and Dependent Vectors - Examples with Solutions
Page Content
Definition of Linearly Independent Vectors
If we can express vector u1
as a linear combinations of the vectors u2 and u3 , we say that these 3 vectors are linearly dependent.
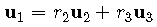
which may be written as
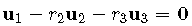
Hence the following definition
Given a set of vectors 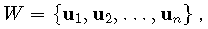
If the equation

has only one trivial solution  , we say that W is a set of linearly independent vectors.
, we say that W is a set of linearly independent vectors.
If the above equation has other solutions, then W is a set of lineraly dependent vectors.
More testing for linearity of vectors in a Subspace are included.
Examples with Solutions
Note solve the examples in the order that they are presented in order to fully understand them.
Example 1
Show that the vectors
\( \) \( \) \( \)
\( \textbf{u}_1 = \begin{bmatrix}
1 \\
3
\end{bmatrix}
\)
and
\( \textbf{u}_2 = \begin{bmatrix}
-5 \\
-15
\end{bmatrix}
\)
are linearly dependent.
Solution to Example 1
Two ways to answer this question
1)
There is an obvious relationship between \( \textbf{u}_1 \) and \( \textbf{u}_2 \) which is
\( \textbf{u}_2 = - 5 \textbf{u}_1 \)
and therefore the two vectors are linearly dependent.
2)
Let us now use the definition to prove that the two vectors are linearly dependent.
Equation (I) given in the definition above is written as
\( r_ 1 \begin{bmatrix}
1 \\
3
\end{bmatrix}
+
r_2 \begin{bmatrix}
-5 \\
-15
\end{bmatrix} = \begin{bmatrix}
0 \\
0
\end{bmatrix} \) (II)
Scalar multiply and add the left side of the above equation to write a system of equations
\( \begin{bmatrix}
r_1 - 5 r_2\\
3 r_1 - 15 r_2
\end{bmatrix}
= \begin{bmatrix}
0 \\
0
\end{bmatrix} \)
We now need to solve the above system. Let us use the method of elimination. Multiply the top equation by \( - 3 \)
\( \begin{bmatrix}
- 3 r_1 + 15 r_2\\
3 r_1 - 15 r_2
\end{bmatrix}
= \begin{bmatrix}
0 \\
0
\end{bmatrix} \)
Add the top and bottom equation and place it at the bottom
\( \begin{bmatrix}
- 3 r_1 + 15 r_2\\
0 + 0
\end{bmatrix}
= \begin{bmatrix}
0 \\
0
\end{bmatrix} \)
The second equation may be used to write that \( r_2 = t \) such that \( t \) is any real number.
Use the top equation to find
\( r_1 = 5 r_2 = 5 t \)
Equation (II) of the definition above has many solutions and therefore vectors \( \textbf{u}_1 \) and \( \textbf{u}_2 \) given above are linearly dependent.
Example 2
Show that the vectors
\( \textbf{u}_1 = \begin{bmatrix}
1 \\
0 \\
1
\end{bmatrix}
\)
,
\( \textbf{u}_2 = \begin{bmatrix}
0 \\
1 \\
2
\end{bmatrix}
\)
and
\( \textbf{u}_3 = \begin{bmatrix}
-2 \\
3 \\
0
\end{bmatrix}
\)
are linearly independent.
Solution to Example 2
Use definition to prove that the two vectors are linearly independent.
Equation (I) given in the definition above is written as
\( r_1 \begin{bmatrix}
1 \\
0 \\
1
\end{bmatrix}
+ r_2
\begin{bmatrix}
0 \\
1 \\
2
\end{bmatrix}
+ r_3
\begin{bmatrix}
-2 \\
3 \\
0
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}
\)
It is a homogeneous system of equation. Using matrices, it may be written as
\( \begin{bmatrix}
1 & 0 & -2\\
0 & 1 & 3 \\
1 & 2 & 0
\end{bmatrix}
\begin{bmatrix}
r_1 \\
r_2 \\
r_3
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}
\)
The above system of equations has a trivial solution \( r_1 =0 , r_2 = 0 , r_3 = 0 \) only if the determinant of the square coefficient matrix on is NOT equal to zero.
\( \text{Det} \begin{bmatrix}
1 & 0 & -2\\
0 & 1 & 3 \\
1 & 2 & 0
\end{bmatrix} = -4
\)
Hence the equation of the definition of linearity of vectors has one trivial solution and therefore the vectors are lineraly independent.
Example 3
Find the values of \( m \) for which the vectors
\( \textbf{u}_1 = \begin{bmatrix}
m \\
4 \\
0
\end{bmatrix}
\)
,
\( \textbf{u}_2 = \begin{bmatrix}
1 \\
-1 \\
8
\end{bmatrix}
\)
and
\( \textbf{u}_3 = \begin{bmatrix}
0 \\
-1 \\
m
\end{bmatrix}
\)
are linearly dependent.
Solution to Example 3
We use the equation of linearity given in the definition
\( r_1 \begin{bmatrix}
m \\
4 \\
0
\end{bmatrix}
+ r_2
\begin{bmatrix}
1 \\
-1 \\
8
\end{bmatrix}
+ r_3
\begin{bmatrix}
0 \\
-1 \\
m
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}
\)
The above system of homogeneous equations in matrix form as
\( \begin{bmatrix}
m & 1 & 0\\
4 & -1 & -1 \\
0 & 8 & m
\end{bmatrix}
\begin{bmatrix}
r_1 \\
r_2 \\
r_3
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}
\)
The determinant of the square matrix is given by
\( \text{Det} \begin{bmatrix}
m & 1 & 0\\
4 & -1 & -1 \\
0 & 8 & m
\end{bmatrix} = - m^2 + 4 m \)
For the vectors to be linearly dependent, the system of equations must have more than one (the trivial) solution and hence the determinant must be equal to 0. Hence
\( - m^2 + 4 m = 0 \)
Solve the above form \( m \)
\( m = 0 \) and \( m = 4 \) are the values for which the given vectors are linearly dependent.
Example 4
Are the vectors
\( \textbf{u}_1 = \begin{bmatrix}
1 \\
1\\
0 \\
-1
\end{bmatrix}
\)
,
\( \textbf{u}_2 = \begin{bmatrix}
5 \\
5 \\
0 \\
0
\end{bmatrix}
\)
and
\( \textbf{u}_3 = \begin{bmatrix}
0 \\
0 \\
-1 \\
-1
\end{bmatrix}
\)
linearly dependent or independent?
Solution to Example 4
Write the equation of linearity given in the definition above
\( r_1 \begin{bmatrix}
1 \\
1 \\
0 \\
-1
\end{bmatrix}
+ r_2
\begin{bmatrix}
5\\
5\\
0 \\
0
\end{bmatrix}
+ r_3
\begin{bmatrix}
0 \\
0 \\
-1 \\
-1
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
0
\end{bmatrix}
\)
Write the above as a system of homogeneous equations
\( \begin{bmatrix}
1 & 5 & 0\\
1 & 5 & 0 \\
0 & 0 & -1 \\
-1 & 0 & -1
\end{bmatrix}
\begin{bmatrix}
r_1 \\
r_2 \\
r_3
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
0
\end{bmatrix}
\)
The row reduced form of the above system of equations is written as
\( \begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
r_1 \\
r_2 \\
r_3
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
0
\end{bmatrix}
\)
which corresponds to the system
\(
\begin{array}{lcl} r_1 & = & 0 \\
r_2 & = & 0 \\
r_3 & = & 0 \\
0 & = & 0
\end{array}
\)
The equation of linearity has only the trivial solution \( r_1 = 0 , r_2 = 0 , r_3 = 0 \) and therefore the vectors \( \textbf{u}_1 \) , \( \textbf{u}_2 \) and \( \textbf{u}_3 \) are linearly independent.
More References and links
- Testing for Linearity of Vectors in a Subspace - Examples with Solutions
- Linear Algebra - Questions with Solutions
- Linear Algebra and its Applications - 5 th Edition - David C. Lay , Steven R. Lay , Judi J. McDonald
- Elementary Linear Algebra - 7 th Edition - Howard Anton and Chris Rorres