Logarithmic Functions

Q: What is a logarithmic function?

A logarithmic function with base B is the inverse of the exponential function with the same base. It is defined as y = log_B(x) if and only if x = B^y, where B > 0, B ≠ 1, and x > 0.

Q: What is the domain and range of a logarithmic function?

The domain of f(x) = log_B(x) is (0, +∞) because the argument of a logarithm must be strictly positive. The range is (-∞, +∞) because the logarithm produces every real number.

Q: Why does a logarithmic function have a vertical asymptote?

The vertical asymptote occurs at x = 0 because as x approaches 0 from the right, log_B(x) approaches -∞ if B > 1 (or +∞ if 0 < B < 1). The argument x must remain positive, so the graph never crosses x = 0.

Q: What is the difference between log and ln?

log(x) usually denotes the common logarithm with base 10, while ln(x) denotes the natural logarithm with base e ≈ 2.71828. Both follow the same logarithmic rules but use different bases.

Q: When is a logarithmic function increasing or decreasing?

If the base B > 1, the logarithmic function is strictly increasing. If 0 < B < 1, the function is strictly decreasing. In both cases, the domain is (0, +∞) and the range is (-∞, +∞).

Q: How do you evaluate a logarithm with an arbitrary base?

Use the change of base formula: log_b(x) = log_a(x) / log_a(b), where a is any convenient base (typically 10 or e). For example, log_2(x) = ln(x) / ln(2).

Q: Do all logarithmic graphs pass through the same point?

Yes. Every logarithmic function of the form f(x) = log_B(x) passes through the point (1, 0), because log_B(1) = 0 for any valid base B. Logarithmic functions have no y-intercept.

This tutorial covers the fundamentals of logarithmic functions. You will learn the formal definition, how to evaluate and graph these functions, their essential mathematical properties (such as domains and asymptotes), and how to apply the change of base formula.

Table of Contents

Definition of Logarithmic Functions

The logarithmic function with base \( B \) is defined as the inverse of the exponential function with the same base.

Formal Definition:

For \( B \gt 0 \) and \( B \neq 1 \),

\[ y = \log_B(x) \quad \text{if and only if} \quad x = B^y \]

Domain restriction: \( x \gt 0 \).

The logarithm with base \( e \) (Euler's number, approximately 2.71828) is called the natural logarithm and is written as \( \ln(x) \).

Because the argument of a logarithm must be strictly positive, the domain of the logarithmic function \( y = \log_B(x) \) is the set of all positive real numbers:

\[ x \gt 0 \quad \text{or equivalently} \quad (0, +\infty) \]

Note: The base \( B \) must satisfy \( B \gt 0 \) and \( B \neq 1 \). If \( B = 1 \), then \( B^y = 1 \) for all \( y \), so \( \log_1 \) would not be a well-defined function.

Evaluating Logarithmic Functions

Logarithms can be evaluated using their inverse relationship with exponential functions. A logarithm simply represents the exponent to which the base must be raised to obtain a given number.

Since \( 2^4 = 16 \), we have \( \log_2(16) = 4 \).
Since \( \sqrt{9} = 3 \), which can be written as \( 9^{\frac{1}{2}} = 3 \), we have \( \log_9(3) = \frac{1}{2} \).
Since \( B^0 = 1 \) (for any base \( B \gt 0, B \neq 1 \)), we always have \( \log_B(1) = 0 \).
Since \( B^1 = B \), we always have \( \log_B(B) = 1 \).
Since \( 10^3 = 1000 \), we have \( \log_{10}(1000) = 3 \).
Since \( e^1 = e \), we have \( \ln(e) = 1 \).
Since \( e^0 = 1 \), we have \( \ln(1) = 0 \).

Key identity: \( \log_B(B^y) = y \) for any real \( y \), and \( B^{\log_B(x)} = x \) for any \( x \gt 0 \).

Graphing Logarithmic Functions

Example 1: Logarithmic Functions with Base Greater Than 1 (\( B \gt 1 \))

Show Graph and Table

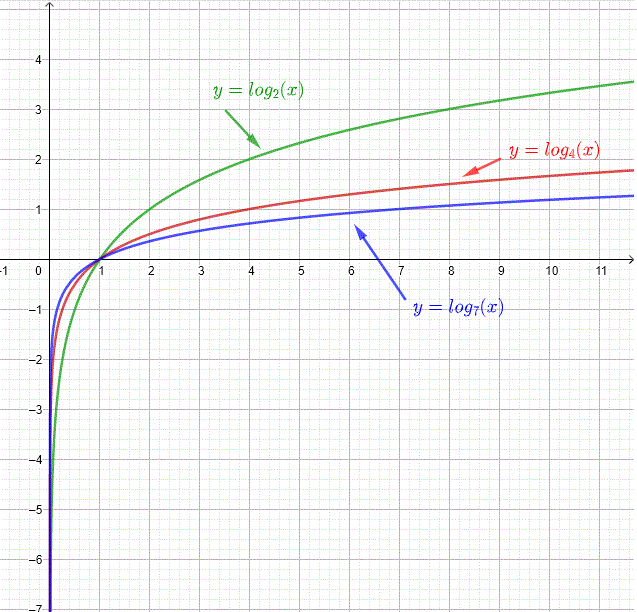
The table and graph below show the logarithmic functions \( \log_2(x) \), \( \log_4(x) \), and \( \log_7(x) \). Notice how all three curves increase as \( x \) gets larger and cross the x-axis at \( (1, 0) \).

\( x \)	\( \log_2(x) \)	\( \log_4(x) \)	\( \log_7(x) \)
\( 10^{-8} \)	\( -26.5754 \)	\( -13.2877 \)	\( -9.4663 \)
\( 0.001 \)	\( -9.9657 \)	\( -4.9828 \)	\( -3.5498 \)
\( 0.01 \)	\( -6.6438 \)	\( -3.3219 \)	\( -2.3665 \)
\( 0.1 \)	\( -3.3219 \)	\( -1.6609 \)	\( -1.1833 \)
\( 0.5 \)	\( -1 \)	\( -0.5 \)	\( -0.3562 \)
\( 1 \)	\( 0 \)	\( 0 \)	\( 0 \)
\( 2 \)	\( 1 \)	\( 0.5 \)	\( 0.3562 \)
\( 100 \)	\( 6.6438 \)	\( 3.3219 \)	\( 2.3665 \)
\( 1000 \)	\( 9.9657 \)	\( 4.9828 \)	\( 3.5498 \)

Graphs of logarithmic functions with base greater than 1, all increasing and passing through (1,0)

Example 2: Logarithmic Functions with Base Less Than 1 (\( 0 \lt B \lt 1 \))

Show Graph and Table

The table and graph below show the logarithmic functions \( \log_{0.2}(x) \), \( \log_{0.5}(x) \), and \( \log_{0.8}(x) \). Notice that when the base is between 0 and 1, the logarithmic curve decreases as \( x \) gets larger.

\( x \)	\( \log_{0.2}(x) \)	\( \log_{0.5}(x) \)	\( \log_{0.8}(x) \)
\( 10^{-8} \)	\( 11.4454 \)	\( 26.5754 \)	\( 82.5508 \)
\( 0.001 \)	\( 4.2920 \)	\( 9.9657 \)	\( 30.9565 \)
\( 0.01 \)	\( 2.8613 \)	\( 6.6438 \)	\( 20.6377 \)
\( 0.1 \)	\( 1.4306 \)	\( 3.3219 \)	\( 10.3188 \)
\( 0.5 \)	\( 0.4306 \)	\( 1 \)	\( 3.1062 \)
\( 1 \)	\( 0 \)	\( 0 \)	\( 0 \)
\( 2 \)	\( -0.4306 \)	\( -1 \)	\( -3.1062 \)
\( 10 \)	\( -1.4306 \)	\( -3.3219 \)	\( -10.3188 \)
\( 100 \)	\( -2.8613 \)	\( -6.6438 \)	\( -20.6377 \)

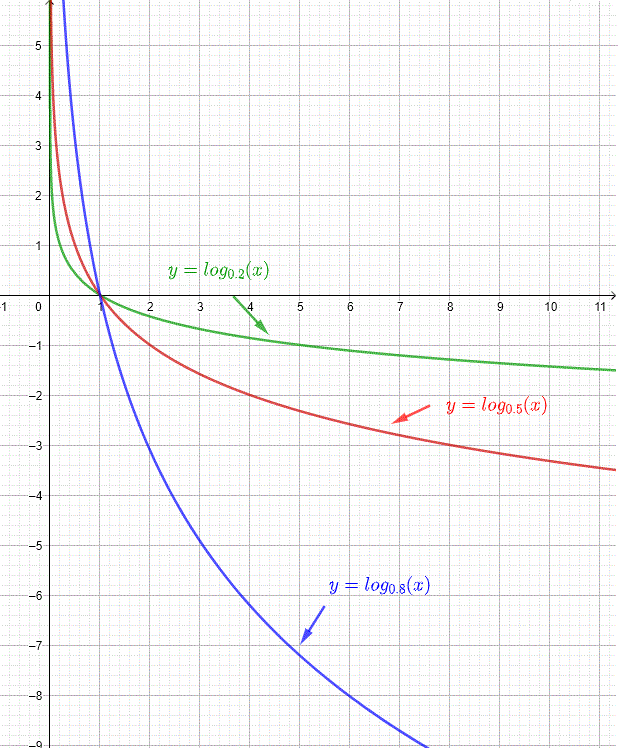
Graphs of logarithmic functions with base less than 1, all decreasing and passing through (1,0)

Properties of Logarithmic Functions

Based on the formal definitions and the graphs analyzed above, we can outline the following key properties of logarithmic functions \( f(x) = \log_B(x) \):

The domain of \( f(x) = \log_B(x) \) is strictly positive: \( (0, +\infty) \).
The range of \( f(x) = \log_B(x) \) covers all real numbers: \( (-\infty, +\infty) \).
The vertical line \( x = 0 \) (the y-axis) serves as a vertical asymptote for the graph.
All basic logarithmic graphs intersect the x-axis at the point \( (1, 0) \). They have no y-intercept.
If the base \( B \gt 1 \), the function is strictly increasing: \[ \lim_{x \to +\infty} \log_B(x) = +\infty \quad \text{and} \quad \lim_{x \to 0^+} \log_B(x) = -\infty \]
If the base \( 0 \lt B \lt 1 \), the function is strictly decreasing: \[ \lim_{x \to +\infty} \log_B(x) = -\infty \quad \text{and} \quad \lim_{x \to 0^+} \log_B(x) = +\infty \]

Properties Summary Table

Property	\( B \gt 1 \)	\( 0 \lt B \lt 1 \)
Domain	\( (0, +\infty) \)	\( (0, +\infty) \)
Range	\( (-\infty, +\infty) \)	\( (-\infty, +\infty) \)
Vertical asymptote	\( x = 0 \)	\( x = 0 \)
\( x \)-intercept	\( (1, 0) \)	\( (1, 0) \)
Monotonicity	Increasing	Decreasing
\( \lim_{x \to 0^+} f(x) \)	\( -\infty \)	\( +\infty \)
\( \lim_{x \to +\infty} f(x) \)	\( +\infty \)	\( -\infty \)

Change of Base Formula

To evaluate or graph a logarithm with an arbitrary base \( b \) using a standard calculator, you can change it to a more convenient base \( a \) (usually base 10 or base \( e \)) using this formula:

\[ \log_b(x) = \frac{\log_a(x)}{\log_a(b)} \]

Valid for \( b \gt 0 \), \( b \neq 1 \), \( a \gt 0 \), \( a \neq 1 \), and \( x \gt 0 \).

For example, you can rewrite a base-2 logarithm using the natural logarithm (\( \ln \)) or the common logarithm (\( \log_{10} \)):

\[ \log_2(x) = \frac{\ln(x)}{\ln(2)} = \frac{\log_{10}(x)}{\log_{10}(2)} \]

Worked example: Evaluate \( \log_5(100) \).

\[ \log_5(100) = \frac{\ln(100)}{\ln(5)} = \frac{4.60517}{1.60944} \approx 2.8614 \]

Check: \( 5^{2.8614} \approx 100 \) ✓

Note: In calculus, logarithms are frequently converted to natural logarithms because the derivative and integral rules for base \( e \) are much simpler to work with. For example, \( \dfrac{d}{dx} \log_a(x) = \dfrac{1}{x \ln a} \).

Common Mistakes to Avoid

Confusing the base with the argument. In \( \log_B(x) \), \( B \) is the base and \( x \) is the argument. The argument must be positive, not the base (though the base must also be positive and not equal 1).
Writing \( \log(x) \) when the base is not 10. \( \log(x) \) by convention means \( \log_{10}(x) \). If the base is different, write it explicitly.
Assuming \( \log(x + y) = \log(x) + \log(y) \). This is false. The product rule is \( \log(xy) = \log(x) + \log(y) \).
Forgetting the domain. After solving a logarithmic equation, always verify that the argument is strictly positive.
Using \( B = 1 \) as a base. \( \log_1(x) \) is undefined, since \( 1^y = 1 \) for all \( y \).

Frequently Asked Questions

What is a logarithmic function?

A logarithmic function with base \( B \) is the inverse of the exponential function with the same base. It is defined as \( y = \log_B(x) \) if and only if \( x = B^y \), where \( B \gt 0 \), \( B \neq 1 \), and \( x \gt 0 \).

What is the domain and range of a logarithmic function?

The domain of \( f(x) = \log_B(x) \) is \( (0, +\infty) \) because the argument of a logarithm must be strictly positive. The range is \( (-\infty, +\infty) \) because the logarithm produces every real number.

Why does a logarithmic function have a vertical asymptote?

The vertical asymptote occurs at \( x = 0 \) because as \( x \) approaches 0 from the right, \( \log_B(x) \) approaches \( -\infty \) if \( B \gt 1 \) (or \( +\infty \) if \( 0 \lt B \lt 1 \)). The argument \( x \) must remain positive, so the graph never crosses \( x = 0 \).

What is the difference between \( \log \) and \( \ln \)?

\( \log(x) \) usually denotes the common logarithm with base 10, while \( \ln(x) \) denotes the natural logarithm with base \( e \approx 2.71828 \). Both follow the same logarithmic rules but use different bases.

When is a logarithmic function increasing or decreasing?

If the base \( B \gt 1 \), the logarithmic function is strictly increasing. If \( 0 \lt B \lt 1 \), the function is strictly decreasing. In both cases, the domain is \( (0, +\infty) \) and the range is \( (-\infty, +\infty) \).

How do you evaluate a logarithm with an arbitrary base?

Use the change of base formula: \( \log_b(x) = \dfrac{\log_a(x)}{\log_a(b)} \), where \( a \) is any convenient base (typically 10 or \( e \)). For example, \( \log_2(x) = \dfrac{\ln(x)}{\ln(2)} \).

Do all logarithmic graphs pass through the same point?

Yes. Every logarithmic function of the form \( f(x) = \log_B(x) \) passes through the point \( (1, 0) \), because \( \log_B(1) = 0 \) for any valid base \( B \). Logarithmic functions have no y-intercept.