Polynomial Problems with Detailed Solutions - Find Coefficients, Zeros, and Analyze Graphs
This page presents 7 polynomial questions and problems designed to help students learn and practice key concepts in algebra. Problems include finding coefficients, zeros, and y- and x-intercepts, analyzing graphs, determining the degree and leading coefficient, and understanding multiplicity of zeros. Each problem is accompanied by detailed, step-by-step solutions to help you fully understand how to solve polynomial functions.
Problem 1: Find the coefficients of a cubic polynomial from its graph
The graph of a cubic polynomial \[ y = ax^{3} + bx^{2} + cx + d \] is shown below. Find the coefficients \(a, b, c, \text{ and } d\).
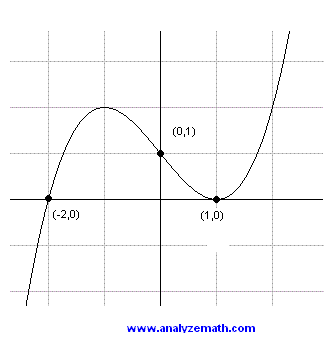
This polynomial has a zero of multiplicity 1 at \( x = -2 \) and a zero of multiplicity 2 at \( x = 1 \). Hence the polynomial may be written as \[ y = a(x+2)(x-1)^2 \] This polynomial has a y-intercept \( (0,1) \). Hence \[ 1 = a(0+2)(0-1)^2 \] Solve for \( a \) to obtain \[ a = \tfrac{1}{2} \] The polynomial may now be written as follows \[ y = \tfrac{1}{2}(x+2)(x-1)^2 \] Expand to obtain \[ y = \tfrac{1}{2}x^3 - \tfrac{3}{2}x + 1 \] We now identify the coefficients as follows \[ a = \tfrac{1}{2}, \quad b = 0, \quad c = -\tfrac{3}{2}, \quad d = 1 \]
Problem 2: Find the coefficients of a quartic polynomial from its graph
The graph of the polynomial \[ y = ax^{4} + bx^{3} + cx^{2} + dx + e \] is shown below. Find the coefficients \(a, b, c, d,\) and \(e\).
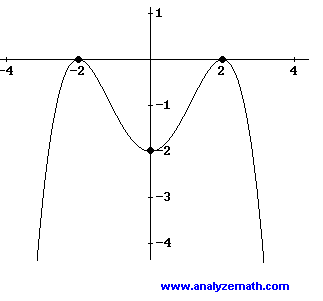
This polynomial has a zero of multiplicity 2 at \(x=-2\) and a zero of multiplicity 2 at \(x=2\). Hence it may be written as \[ y = a(x+2)^2(x-2)^2 \] We now use the \(y\)-intercept at \((0,-2)\) to write the equation \[ -2 = a(0+2)^2(0-2)^2 \] Solve the above for \(a\) to obtain \[ a = -\frac{1}{8} \] We now write the polynomial as follows \[ y = \left(-\frac{1}{8}\right)(x+2)^2(x-2)^2 \] Expand \[ y = -\frac{1}{8}x^4 + x^2 - 2 \] We now identify the coefficients \[ a = -\frac{1}{8}, \quad b = 0, \quad c = 1, \quad d = 0, \quad e = -2 \]
Problem 3: Find the other real zeros of a degree 6 polynomial with a given double zero
The polynomial \[ f(x) = x^6 + 4x^5 + x^4 - 12x^3 - 11x^2 + 4x + 4 \] has a zero of multiplicity 2 at \(x = -2\). Find the other real zeros.
If \(f\) has a zero of multiplicity 2, then it may be written as follows: \[ f(x) = (x + 2)^2 Q(x) \] where \(Q(x)\) is a polynomial of degree 4 and may be found by division: \[ Q(x) = \frac{f(x)}{(x + 2)^2} = x^4 - 3x^2 + 1 \] The polynomial \(f\) may now be written as: \[ f(x) = (x + 2)^2 (x^4 - 3x^2 + 1) \] The remaining zeros of the polynomial \(f\) may be found by solving the equation: \[ x^4 - 3x^2 + 1 = 0 \] It is an equation of quadratic type with solutions: \[ x_1 = \frac{\sqrt{5} + 1}{2}, \quad x_2 = \frac{\sqrt{5} - 1}{2}, \quad x_3 = \frac{-\sqrt{5} - 1}{2}, \quad x_4 = \frac{-\sqrt{5} + 1}{2} \]
Problem 4: Find remaining zeros of a quartic polynomial with given irrational zeros
The polynomial \[ f(x) = 3x^4 + 5x^3 - 17x^2 - 25x + 10 \] has irrational zeros at \(+\sqrt{5}\) and \(-\sqrt{5}\). Find the other zeros.
The polynomial \(f\) may be written as \[ f(x) = (x + \sqrt{5})(x - \sqrt{5}) Q(x) = (x^2 - 5) Q(x) \] where \(Q(x)\) may be found by division: \[ Q(x) = \frac{f(x)}{x^2 - 5} = 3x^2 + 5x - 2 \] Hence, \(f(x)\) may be written as \[ f(x) = (x^2 - 5)(3x^2 + 5x - 2) \] The remaining zeros may be found by solving the equation \[ 3x^2 + 5x - 2 = 0 \] Solve the above equation to find the remaining zeros of \(f\): \[ x_1 = -2, \quad x_2 = \frac{1}{3} \]
Problem 5: Determine the sign of the y-intercept of a degree 4 polynomial with given zeros
A polynomial of degree 4 has a positive leading coefficient and simple zeros (i.e., zeros of multiplicity 1) at \[ x_1 = 2, \quad x_2 = -2, \quad x_3 = 1, \quad x_4 = -1 \] Is the \(y\)-intercept of the graph of this polynomial positive or negative?
All polynomials with degree 4 and positive leading coefficient will have a graph that rises to the left and to the right. Since the polynomial has two negative zeros and two positive zeros, the only possibility for the \(y\)-intercept is to be positive.
Problem 6: Analyze the graph of a polynomial to determine degree and leading coefficient
The graph of polynomial \(p\) is shown below.

- Is the degree of \(p\) even or odd?
- Is the leading coefficient negative or positive?
- Can you find the degree from the graph of \(p\)? Explain.
- odd
- negative
- No. The degree of a polynomial depends on the real and complex zeros. The graph shows only the real zeros. Hence, not enough information is given to find the degree of the polynomial.
Problem 7: Give reasons why a graph cannot represent a given quartic polynomial
Give 4 different reasons why the graph below cannot be the graph of the polynomial \( P \) given by \[ p(x) = x^4 - x^2 + 1 \]
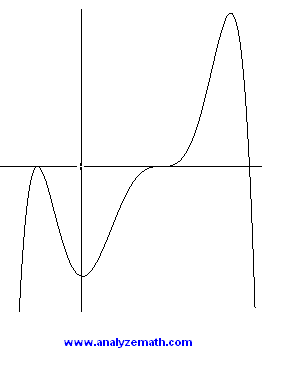
- 1 - The given polynomial has degree 4 and positive leading coefficient and the graph should rise on the left and right sides.
- 2 - \( P(0) = 1 \), graph shows negative value.
- 3 - The equation \( x^4 - x^2 + 1 = 0 \) has no real solutions which suggests that the polynomial \( P(x) = x^4 - x^2 + 1 \) has no real zeros. The graph shows \( x \) intercepts.
- 4 - The graph has a zero of multiplicity 2, a zero of multiplicity 3 and a zero of multiplicity 1. So the degree of the graphed polynomial should be at least 6. The given polynomial has degree 4.