Write Rational Functions: Practice Problems with Solutions on Asymptotes and Zeros
Learn how to write rational functions based on their key characteristics, including vertical and horizontal asymptotes, slant asymptotes, x-intercepts, zeros, and holes. Step-by-step solutions help you master each type of problem.
Problem 1: Rational Function with Vertical and Horizontal Asymptotes
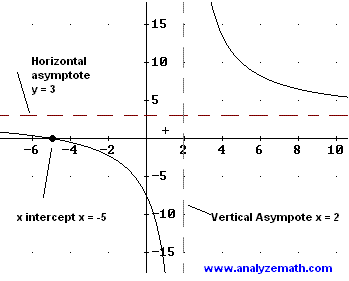
Write a rational function \( f \) that has a vertical asymptote at \( x = 2 \), a horizontal asymptote \( y = 3 \), and a zero at \( x = -5 \).
Since \( f \) has a vertical asymptote at \( x = 2 \), the denominator of the rational function contains the term \( (x - 2) \). Hence, \( f \) has the form \[ f(x) = \frac{g(x)}{x - 2}. \] The numerator \( g(x) \) must be of the same degree as the denominator to ensure a horizontal asymptote, and must contain the term \( (x + 5) \) since \( f \) has a zero at \( x = -5 \). Therefore, \[ f(x) = \frac{3(x + 5)}{x - 2}. \] Check that all the characteristics listed in the problem appear in the graph of \( f \) shown below.
Problem 2: Rational Function with Two Vertical Asymptotes and No X-Intercept
Write a rational function \( g \) with vertical asymptotes at \( x = 3 \) and \( x = -3 \), a horizontal asymptote at \( y = -4 \), and with no x-intercept.
Since \( g \) has vertical asymptotes at \( x = 3 \) and \( x = -3 \), the denominator contains the product \( (x - 3)(x + 3) \). Hence, \[ g(x) = \frac{h(x)}{(x - 3)(x + 3)}. \] To achieve the horizontal asymptote \( y = -4 \), the numerator \( h(x) \) must be of the same degree as the denominator with leading coefficient \(-4\). To have no real zeros, we can take \[ g(x) = \frac{-4x^2 - 6}{(x - 3)(x + 3)}. \] Check the characteristics in the graph of \( g \) shown below.

Problem 3: Rational Function with Hole and Vertical Asymptote
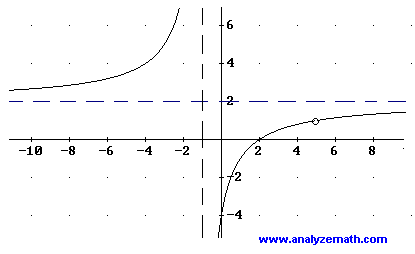
Write a rational function \( h \) with a hole at \( x = 5 \), a vertical asymptote at \( x = -1 \), a horizontal asymptote at \( y = 2 \), and an x-intercept at \( x = 2 \).
Since \( h \) has a hole at \( x = 5 \), both the numerator and denominator have a factor \( (x - 5) \). The vertical asymptote at \( x = -1 \) gives a factor \( (x + 1) \) in the denominator, and the x-intercept at \( x = 2 \) gives a factor \( (x - 2) \) in the numerator. To satisfy the horizontal asymptote \( y = 2 \), the numerator and denominator must have the same degree and the ratio of leading coefficients must be 2. Hence, \[ h(x) = \frac{2(x - 5)(x - 2)}{(x - 5)(x + 1)}. \] The graph of \( h \) is shown below; check the characteristics.
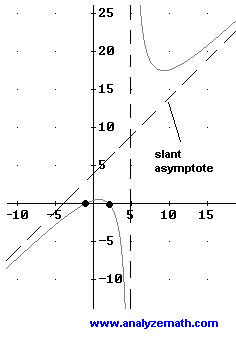
Problem 4: Rational Function with Slant Asymptote
Write a rational function \( f \) with a slant asymptote \( y = x + 4 \), a vertical asymptote at \( x = 5 \), and one of the zeros at \( x = 2 \).
The graph of \( f \) has a slant asymptote \( y = x + 4 \) and a vertical asymptote at \( x = 5 \). Hence, \( f(x) \) can be written as \[ f(x) = (x + 4) + \frac{a}{x - 5}, \] where \( a \) is a constant determined from the zero at \( x = 2 \): \[ f(2) = (2 + 4) + \frac{a}{2 - 5} = 0 \implies a = 18. \] Therefore, \[ f(x) = (x + 4) + \frac{18}{x - 5} = \frac{x^2 - x - 2}{x - 5}. \] Check the characteristics of the graph of \( f \) shown below.