1 - Numbers
Solutions
- \( (5 + 4) + 1 = 5 + (4 + 1) \) : associativity of addition
- \( 2(4 + 7) = 2 \times 4 + 2 \times 7 \) : distributivity
- \( 11 + 9 = 9 + 11 \) : commutativity of addition
- \( 33 + 0 = 33 \) : identity of addition
- \( 5 \times 1 = 5 \) : identity of multiplication
- \( 9 \times 6 = 6 \times 9 \) : commutativity of multiplication
- \( (7 - 2) \times 6 = 7 \times 6 - 2 \times 6 \) : distributivity
- \( 3 \times 6 - 3 \times 2 = 3(6 - 2) \) : distributivity in reverse (factoring)
\( \color{red}{2,3,5,7,11} \) are prime numbers
Hundreds
- \( (9 - 3) + 2 = 6 + 2 = 8 \)
- \( 7 - (5 - 2) = 7 - 3 = 4 \)
- \( (3 + 7) \times 3 = 10 \times 3 = 30 \)
- \( (8 - 2) \times 3 = 6 \times 3 = 18 \)
\( 8 \)
Rules of rounding
- If the digit in the tenths is less than 5 , remove all digits after the decimal point without changing the ones digit.
- If the tenths digit is equal to 5 or more, remove all digits after the decimal point and add 1 the ones digit.
Applications
- \( 0.41 \) rounded to the nearest whole number is equal to \( \color{red}{0} \) because the first digit after the decimal point is equal to \( 4 \), and therefore less than \( 5 \) (rule 1 above).
- \( 1.2999 \) rounded to the nearest whole number is equal to \( \color{red}{1} \) because the first digit after the decimal point is equal to \( 2 \), and therefore less than \( 5 \) (rule 1 above).
- \( 123.5 \) rounded to the nearest whole number is equal to \( \color{red}{124} \) because the first digit after the decimal point is equal to \( 5 \), and therefore greater than or equal to \( 5 \) (rule 2 above).
- \( 0.1 > 0.3 \) : false
- \( 1.2 \lt 1.3 \) : true
- \( 0.5 \lt 0.05 \) : false
- \(0.4 \times 3 = 1.2 \)
- \(8 - 3 \times 0.2 = 7.4 \)
- \(0.5 \div 5 = 0.1 \)
2 - Factors, Multiples and Divisibility of Numbers
Solutions
- The factors of 8 are : 1,2,4,8
- The factors of 12 are : 1,2,3,4,6,12
- The common factors of 8 and 12 are : 1, 2, 4
- The greatest of the above common factors is : 4
- Hence the GCF of 8 and 12 is equal to \( \color{red}4 \).
- Multiples of 3 are : \( 3, 6, 9, 12, 15, 18, \color{red}{21} , 24 , 27 , ...\)
- Multiples of 7 are : \( 7, 14, \color{red}{21} , 28 , ... \)
- The common and smallest common multiple of 3 and 7 is equal to 21 .
Rule: Any number with the last digit on the right (ones place value) equal to \( 0 \) or \( 5 \) is divisible by \( 5 \). Hence
\( 12\color{red}5 \; \) and \( \; 20\color{red}0 \) are divisible by \( 5 \).
Rule: Any number with the last digit on the right (ones place value) equal to \( 0, 2, 4, 6 \) or \( 8 \) is divisible by \( 2 \).
\( 28\color{red}0 \; \) and c) \( \; 47\color{red}6 \) are divisible by \( 2 \).
Rule: Any number whose digits add up to a number divisible by \( 3 \) is divisible by \( 3 \).
- The sum of the digits in \( 105 \) is given by : \( 1+0+5 = \color{red}6\) and because \( \color{red}6 \) is divisible by \( 3 \), the given number \( 105 \) is divisible by \( 3 \).
- The sum of the digits in \( 101 \) is given by : \( 1+0+1 = \color{red}2 \) and because \( \color{red}2 \) is NOT divisible by \( 3 \), the given number \( 101 \) is NOT divisible by \( 3 \).
- The sum of the digits in \( 234 \) is given by : \( 2+3+4 = \color{red}9 \) and because \( \color{red}9 \) is divisible by \( 3 \), the given number \( 234 \) is divisible by \( 3 \).
3 - Fractions and Mixed Numbers
Solutions
Definition: A fraction whose numerator is greater than or equal to its denominator is an improper fraction.
b) \( \dfrac{10}{3} \) and c) \( \dfrac{3}{3} \) are improper fractions.
- \( \dfrac{7}{5} = \dfrac{5+2}{5} = \dfrac{5}{5} + \dfrac{2}{5} = 1 \dfrac{2}{5} \)
- \( \dfrac{8}{3} = \dfrac{3+3+2}{3} \\~\\ \qquad = \dfrac{3}{3} + \dfrac{3}{3} + \dfrac{2}{3} = 1 + 1+ \dfrac{2}{3} \\~\\ \qquad = 2 \dfrac{2}{3} \)
- \( \dfrac{9}{2} = \dfrac{2+2+2+2+1}{2} \\~\\ \qquad = \dfrac{2}{2} + \dfrac{2}{2} + \dfrac{2}{2} + \dfrac{2}{2} + \dfrac{1}{2} \\~\\ \qquad = 1+1+1+1+ \dfrac{1}{2} = 4 \dfrac{1}{2}\)
Rule: If we multiply (or divide) the numerator and denominator of a given fraction by the same number, we obtain a new fraction equivalent to the given fraction.
- The given fractions have known denominators \( 2 \) and \( 4\): we need to multiply the denominator \( 2 \) by \( 2 \) in order to obtain the denominator \( 4 \)
Hence
Multiply the numerator and the denominator of the fraction \( \dfrac{1}{2} \) by \( 2 \) to obtain an equivalent fraction \( \dfrac{1 \times 2}{2 \times 2} = \dfrac{\color{red}2}{4} \)
For the given pairs of fractions to be equivalent, the missing numerator must be equal to \( \color{red}2 \) - The given fractions have known numerators \( 2 \) and \( 6\): we need to multiply the numerator \( 2 \) by \( 3 \) in order to obtain the numerator \( 6 \)
Hence
Multiply the numerator and the denominator of the fraction \( \dfrac{2}{5} \) by \( 3 \) to obtain an equivalent fraction \( \dfrac{2 \times 3}{5 \times 3} = \dfrac{6}{\color{red}{15}} \)
For the given pairs of fractions to be equivalent, the missing denominator must be equal to \( \color{red}{15} \) - The given fractions have known denominators \( 3 \) and \( 9\): we need to multiply the denominator \( 3 \) by \( 3 \) in order to obtain the denominator \( 9 \)
Hence
Multiply the numerator and the denominator of the fraction \( \dfrac{1}{3} \) by \( 3 \) to obtain an equivalent fraction \( \dfrac{1 \times 3}{3 \times 3} = \dfrac{\color{red}3}{9} \)
For the given pairs of fractions to be equivalent, the missing numerator must be equal to \( \color{red}3 \)
-
The fractions in the expression have the same denominator and therefore we evaluate by subtracting the numerators and keeping the same denominator as follows
\( \dfrac{4}{10} - \dfrac{1}{10} = \dfrac{4-1}{10} = \dfrac{3}{10} \) -
Rewrite the fraction \( \dfrac{1}{2} \) with the denominator \( 4 \) by multiplying its numerator and denominator by \( 2 \)
\( \dfrac{1}{2} + \dfrac{3}{4} = \dfrac{1 \times 2}{2 \times 2 } + \dfrac{3}{4} \)
Simplify
\( = \dfrac{2}{ 4 } + \dfrac{3}{4} \)
Now that the fractions have the same denominator, we add the numerators and evaluate as follows
\( = \dfrac{2+3}{4} = \dfrac{5}{4} \) - Multiplication rule of fractions: Multiply numerators together and numerators together.
\( \dfrac{1}{2} \times \dfrac{2}{3} = \dfrac{1 \times 2}{2 \times 3} \)
Simplify
\( = \dfrac{2}{6} \) - Division rule of fractions: multiply the first fractions by the reciprocal of the second fraction.
\( \dfrac{3}{4} \div \dfrac{1}{2} = \dfrac{3}{4} \times \dfrac{2}{1} \)
Apply the multiplication rule of fractions and simplify.
\( = \dfrac{3 \times 2}{4 \times 1} = \dfrac{6}{4}\) -
Rewrite \( 3 \) as a fraction \( 3 = \dfrac{3}{1} \)
\( \dfrac{3}{4} \div 3 = \dfrac{3}{4} \div \dfrac{3}{1} \)
Use the division of fractions rule
\( = \dfrac{3}{4} \times \dfrac{1}{3} \)
Use multiplication of fractions rule
\( = \dfrac{3 \times 1}{4 \times 3} = \dfrac{3}{12} \) -
Rewrite \( 2 \) as a fraction \( 2 = \dfrac{2}{1} \)
\( 2 \times \dfrac{2}{6} = \dfrac{2}{1} \times \dfrac{2}{6} \)
Use multiplication rule
\( = \dfrac{4}{6} \) -
Add the whole parts of the mixed numbers and the fractions separately
\( 1 \dfrac{1}{4} + 2 \dfrac{1}{4} = (1 + 2 ) + ( \dfrac{1}{4} + \dfrac{1}{4}) = 3 \dfrac{2}{4} \) -
Subtract the whole parts of the mixed numbers and the fractions separately
\( 3 \dfrac{2}{5} - 1 \dfrac{1}{5} = (3-1) + ( \dfrac{2}{5} - \dfrac{1}{5}) = 3 \dfrac{1}{5}\)
Write as a decimal
- \( \dfrac{7}{10} = 7 \div 10 = 0.7 \)
- \( \dfrac{17}{100} = 17 \div 100 = 0.17\)
- \( 1 \dfrac{1}{4} \)
- \( \dfrac{1}{4} \)
- \( 3 \dfrac{3}{8} \)
4 - Exponents
Solutions
- \( 2 \times 2 \times 2 \times 2 \times 2 = 2^5 \)
- Five squared: \( 5^2 \)
- \( 4 \) cubed: \( 4^3 \)
- \( 6 \) to the seventh power: \( 6^7 \)
- \( 2^3 = 2 \times 2 \times 2 = 8 \)
- \( 1^5 = 1 \times 1 \times 1 \times 1 \times 1 = 1 \)
- \( 4^2 = 4 \times 4 = 16 \)
- \( 1000^0 = 1 \) (Any nonzero number to the power \( 0 \) is equal to \( 1 \))
5 - Ratios and Rates
Solutions
- \( 2:3 \)
- \( 3:2 \)
- \( 3:5 \)
- \( 11:8 \)
- \( 8:19 \)
If \( x \) is the number of boys out of the total of \( 600 \) students, then \( 3 x \) is the number of girls out of the total of \( 600 \) students.
The total number of boys and girls is \( 600 \) therefore we may write the equation \[ x + 3x = 600 \] Group like terms on the left side of the equation \[ 4x = 600 \] Divide both sides of the equation by \(4\) \[ 4x \div 4 = 600 \div 4 \] Simplify \( x = 600 \div 4 = 150 \) students are boys.
Check if the answer to the problem makes sense
Number of girls is \( 3 x = 3 \times 150 = 450 \). Hence the total number of boys and girls is equal to \( 150 + 450 = 600 \) which is exactly what is given.
6 - Percent and Related Problems
Solutions
7 - Convert Units of Measurement
Solutions
We convert as follows
\[ 320 \text{ L} = 320 \times \dfrac{1}{100} \text{ hl} = \dfrac{320}{100} \text{ hl} = 3.2 \text{ hl} \]
Convert
\[ 234500 \text{ mm} = 234500 \times \dfrac{1}{1000} \text{ m} = \dfrac{234500}{1000} \text{ m} = 234.5 \text{ m}\]
Hence the conversion
\[ 2300 \text{ m} = 2300 \times \dfrac{1}{1000} \text{ km} = 2.3 \text{ km}\]
8 - Mathematical Expressions
Solutions
Substitute \( a \) and \( b \) by \( 3 \) and \( 2 \) respectively in the given expression \[ a - b = 3 - 2 = 1 \]
Substitute \( x \) by \( 6 \) in the given expression \[ \; \dfrac{2 x}{3} = \dfrac{2 \times 6}{3} = \dfrac{12}{3} = 4 \]
- \( x - 3 \)
- \( 5(x + 2) \)
- \( (2x + 1)^2 \)
- \( 3(x + 1) = 2 \)
- \( 3 \lt x \)
- \( 5 \ge x \)
- \( y \le 9 \)
- \( x - 2 \le -2 \)
- \[ 2(x + 4) = 2 \times x + 2 \times 4 \\[6pt] \qquad = 2x + 8 \]
- \[ 3(a + b + 2) = 3 \times a + 3 \times b + 3 \times 2 \\[6pt] \qquad = 3a + 3b + 6 \]
- \[ \dfrac{1}{4}(8x + 4) = \dfrac{1}{4} \times 8x + \dfrac{1}{4} \times 4 \\[6pt] \qquad = \dfrac{8}{4} \times x + \dfrac{4}{4} = 2x + 1 \]
- \[ 0.2(x + 2) = 0.2 \times x + 0.2 \times 2 \\[6pt] \qquad = 0.2x + 0.4 \]
-
Factors of \( 9 \) are : \( 1, \color{red}3, 9 \)
Factors of \( 6 \) are : \( 1, 2, \color{red}3, 6 \)
The greatest common factor (GCF) of \( 9 \) and \( 6 \) is \( \color{red}3 \)
-
\( 9 = \color{red}3 \times 3 \)
\( 6 = \color{red}3 \times 2 \)
-
\( 9 x + 6 = \color{red}3 \times 3 \times x + \color{red}3 \times 2\)
Use distributive property in reverse ( i.e : \( \color{red}{a \times x + a \times y = a(x+y)} \) ) to factor the given expression.
\( 9 x + 6 = \color{red}3 \times 3 \times x + \color{red}3 \times 2 = \color{red}3 (3 x + 2)\)
9 - Equation with One Variable and Related Problems
Solutions
- Given the equation \( x + 2 = 8\)
Subtract \( 2 \) from both sides of the equation
\( x + 2 \color{red}{- 2} = 8 \color{red}{- 2} \)
Simplify
\( x = 6 \quad \) is the solution of the given equation. - Given the equation \( 2 x = 6 \)
Divide both sides of the equation by \( 2 \)
\( 2 x \color{red}{\div 2} = 6 \color{red}{\div 2} \)
Simplify
\( x = 3 \quad \) is the solution of the given equation. - Given the equation \( x - 3 = 7 \)
Add \( 3 \) from both sides of the equation
\( x - 3 \color{red}{+3} = 8 \color{red}{+3} \)
Simplify
\( x = 11 \quad \) is the solution of the given equation.
-
The formula of the perimeter \( P \) of a rectangular garden of length \( L \) and width \( W \) is given by
\( P = 2 \times L + 2 \times W\)
We substitute \( L, W \) and \( P \) by the given \( L = 3 \), \( W = x \) and \( P = 10 \) into the formula above above
\( 10 = 2 \times 3 + 2 \times x \)
Simplify and rewrite as
\( 2 x + 6 = 10\) -
Subtract \( 6 \) from both sides of the equation
\( 2 x + 6 \color{red}{- 6} = 10 \color{red}{- 6}\)
Simplify
\( 2 x = 4 \)
Divide both sides of the equation by \(2\)
\( 2 x \color{red}{\div 2} = 4 \color{red}{\div 2}\)
Simplify
\( x = 2 \) is the width of the rectangle garden, hence \( W = 2 \) -
One way to check our calculations is to calculate the perimeter of the rectangular garden.
\( P = 2 \times L + 2 \times W \\ \qquad = 2 \times 3 + 2 \times 2 = 6 + 4 = 10 \)
which corresponds to the given perimeter \( P = 10 \).
10 - Coordinate Plane
Solutions
- \( (0,1) \) is located on the positive side of the y-axis
- \( (-2,-3) \) is located in quadrant 3
- \( (2,9) \) is located in quadrant 1
- \( (-4,6) \) is located in quadrant 2
- \( (3,-4) \) is located in quadrant 4
- \( (-3,0) \) is located on the negative side of the x-axis
\( A = (-1,1) \)
\( B = (0,-1) \)
\( C = (2,0) \)
\( D = (3,1) \)
\( E = (-2,-1) \)
\( F= (3,-2) \)
\( G = (0,3) \)
\( H = (0,0) \)
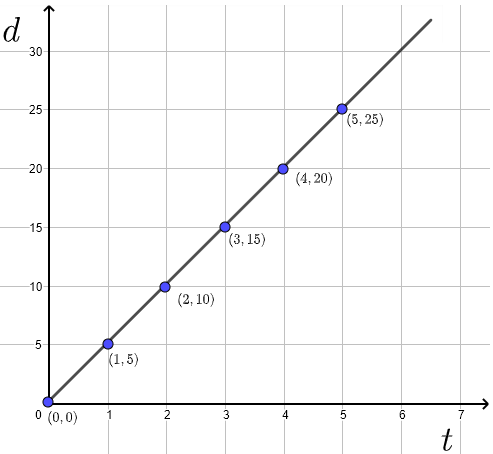
a) For \( t = 0 \) , \( d = 0 \)
For \( t = 1 \) hour, \( d = 5 \) km
For \( t = 2 = 1 + 1 \) hours, \( d = 5 + 5 = 10 \) km
For \( t = 3 = 1 + 1 + 1 \) hours, \( d = 5 + 5 + 5 = 15 \) km
For \( t = 4 = 1 + 1 + 1 + 1 \) hours, \( d = 5 + 5 + 5 + 5 = 20 \) km
For \( t = 5 = 1 + 1 + 1 + 1 + 1 \) hours, \( d = 5 + 5 + 5 + 5 + 5 = 25 \) km

b) The points on the table above are plotted below and the points are joined to give a line.
11 - Inequalities
Solutions
The number line with values involved in the given inequalities is shown below.
 When comparing two numbers using the number, the number on the left is smaller than the number on the right
When comparing two numbers using the number, the number on the left is smaller than the number on the right
- \( -4 \lt 0 \) , true because \( -4 \) is to the left of \( 0 \)
- \( 0 \gt 4 \) , false because \( 0 \) is to the left of \( 4 \)
- \( -6 \lt -4 \) , true because \( -6 \) is to the left of \( -4 \)
- \( -6 \gt 5 \) , false because \( -6 \) is to the left of \( 5 \)
- \( 0 \lt 6 \) , true because \( 0 \) is to the left of \( 6 \)
12 - Geometry
Solutions
b) \( 180^{\circ} \).
In the given figure, angles \( \angle AOB \) and \( \angle BOC \) are
b) Supplementary.
- \( \angle AOB \; \text{and} \; \angle DOF \quad \) , NOT Vertical angles
- \( \angle BOC \; \text{and} \; \angle EOF \quad \) , Vertical angles
- \( \angle COD \; \text{and} \; \angle FOB \) , NOT Vertical angles
- \( \angle FOB \; \text{and} \; \angle COE \quad \) , Vertical angles
- \( \angle AOC \; \text{and} \; \angle DOE \quad \) , NOT Vertical angles
- \( \angle BOD \; \text{and} \; \angle EOA \) , Vertical angles
- Pentagon : 5 sides
- Trapezoid : 4 sides
- Triangle : 3 sides
- Kite : 4 sides
b) Two angles are equal and the opposite sides to the equal angles are equal.
\( \text{Perimeter} = 2 \times \text{length} + 2 \times \text{width} = 2 \times 10 + 2 \times 5 = 20 + 10 = 30 \) cm
Since ABCD is a rectangle, ADE is a right triangle.
The area of the shaded surface may be calculated by subtracting the area of the right triangle ADE from the area of the rectangle ABCD.
Area of right triangle ADE \( \quad = \dfrac{1}{2} \times \overline{DE} \times \overline{AD} = \dfrac{1}{2} \times 2 \times 7 = 7 \) squared centimeters
Area of rectangle ABCD \( \quad = \overline{AB} \times \overline{AD} = 10 \times 7 = 70 \) squared centimeters
Area of shaded surface = Area of rectangle ABCD - Area of right triangle ADE \( \quad = 70 - 7 = 63 \) squared centimeters
Note that the shaded region whose area is calculated above is a trapezoid and its area may be calculated using the formula for the area of a trapezoid.
13 - Three Dimensional Figures
Solutions
Number of Faces \( \quad = 1 + 1 + 4 = 6 \)
a) Area of the rectangles ABCD \( \quad = 6 \times 4 = 24 \) squared units
Area of the rectangles ADHE \( \quad = 4 \times 10 = 40 \) squared units
Area of the rectangles DCGH \( \quad = 6 \times 10 = 60 \) squared units
b)
The surface area \( A \) of the rectangular prism is equal to TWICE the sum of the areas of the rectangles ABCD, ADHE and DCGH.
\( A = 2 \times (24+40+60) = 248 \) squared units
c)
Volume \( \quad = 6 \times 4 \times 10 = 240 \) cubed units
The volume is given by the product of the area \( a \) of the right triangle ABC and the length of the prism \( \overline{AF} \)
Hence the equation \[ 24 = a \times \overline{AF} \] The area \( a \) of the right triangle ABC \( \quad = \dfrac{1}{2} \times 4 \times 3 = 6 \)
Substitute \( a \) by its value in the equation \[ 24 = 6 \; \overline{AF} \] Divide both sides of the equation by \( 6 \) and solve for \( \overline{AF} \) to obtain \[ \overline{AF} = 4\] The total surface area is given by the sum of the areas of all 5 faces : the two right triangles and the 3 rectangles
The total surface area \( \quad = (6 + 6) + (4 \times 4 + 3 \times 4 + 5 \times 4) = 60 \) squared units
14 - Data and Graphs
Solutions
Monday : 3 hours
Tuesday : 3 hours
Wednesday : 2 hours
Thursday : 4 hours
Friday : 3 hours
Total number of hours \( \quad = 3 + 3 + 2 + 4 + 3 = 15 \)
b) From the histogram, \( 7 \) students scored in the range 80-89 and \( 4 \) students scored in the range 60-69.
Hence \( 7 - 4 = 3 \) more students scored in the range 80-89 than students who scored in the range 60-69.
15 - Statistics
Solutions
Smallest data value \( \; = 1 \)
range = Largets data value - Smallest data value \( \; = 7 - 1 = 6 \)
mean \( = \dfrac{1 + 4 + 2 + 2 + 3 + 2 + 7}{7} = \dfrac{21}{7} = 3 \)
mode = the data with the highest frequency of repetition \( \; = 2 \) (listed 3 times)
Order the data values from smallest to the largest \[ \{ 1 , 2 , 2 , \color{red}2 , 3 , 4 , 7 \} \] median is the data value that is located in the middle (red) of the ordred data values \( \; = 2 \)
16 - Probabilities
Solutions
b) -0.5 and c) 2 cannot be measures of probability.
b)
\( \color{blue}5 \) outcomes are possible if you select one of five different cards at random.
c)
\( \color{red}2 \times \color{blue}5 = 10 \) outcomes are possible if you flip a coin and select one of five different cards at random.
a) If you roll a fair die with numbers from 1 to 6 on the faces, there are \( \color{red}6\) possible outcomes : \( \{ 1 , 2 , 3 , 4 , 5 , 6 \} \)
b) It is impossible to obtain 0 because it is not a possible outcome and therefore the probability is equal to 0.
c) There is one 5 out of the 6 outcomes, hence probaility to obtain a number greater than 4 is equal to \( \color{blue}2 / \color{red}6 \) ?
d) There are \( \color{blue}2 \) numbers greater than 4 which are 5 and 6, hence probaility to obtain a number greater than 4 is equal to \( \color{blue}2 / \color{red}6 \) ?