Grade 7 Maths Problems With Solutions

Let's define the total number of balls in the bag as \( N \).

We know that:

\( \dfrac{1}{4} \) of the balls are green: \( \dfrac{N}{4} \)

\( \dfrac{1}{8} \) of the balls are blue: \( \dfrac{N}{8} \)

\( \dfrac{1}{12} \) of the balls are yellow: \( \dfrac{N}{12} \)

The remaining 26 balls are white.

Since all balls add up to \( N \), we can write: \[ \dfrac{N}{4} + \dfrac{N}{8} + \dfrac{N}{12} + 26 = N \]

The least common denominator for 4, 8, and 12 is 24. Converting the fractions: \[ \dfrac{N}{4} = \dfrac{6N}{24}, \quad \dfrac{N}{8} = \dfrac{3N}{24}, \quad \dfrac{N}{12} = \dfrac{2N}{24} \] Rewriting the equation: \[ \dfrac{6N}{24} + \dfrac{3N}{24} + \dfrac{2N}{24} + 26 = N \] \[ \dfrac{6N + 3N + 2N}{24} + 26 = N \] \[ \dfrac{11N}{24} + 26 = N \] Rearrange the equation: \[ 26 = N - \dfrac{11N}{24} \] \[ 26 = \dfrac{24N}{24} - \dfrac{11N}{24} \] \[ 26 = \dfrac{13N}{24} \] Multiply both sides by 24: \[ 26 \times 24 = 13N \] \[ 624 = 13N \] \[ N = 48 \] The number of blue balls is \[ \dfrac{N}{8} = \dfrac{48}{8} = 6 \]

Let \( N \) be the total number of students in the school.

\( 50\% \) of the students are younger than 10, which means: \[ \dfrac{1}{2} N \]

\( \dfrac{1}{20} N \) of the students are 10 years old.

\( \dfrac{1}{10} N \) of the students are older than 10 but younger than 12.

The remaining students, who are 12 years or older, are 70 in number.

Thus, the equation representing the total number of students is: \[ \dfrac{1}{2} N + \dfrac{1}{20} N + \dfrac{1}{10} N + 70 = N \] Rewriting the equation: \[ \dfrac{1}{2} N + \dfrac{1}{20} N + \dfrac{1}{10} N = N - 70 \] Find a common denominator (LCM of 2, 20, and 10 is 20): \[ \dfrac{10}{20} N + \dfrac{1}{20} N + \dfrac{2}{20} N = N - 70 \] \[ \dfrac{13}{20} N = N - 70 \] Rearrange: \[ N - \dfrac{13}{20} N = 70 \] \[ \dfrac{7}{20} N = 70 \] Multiply both sides by \( \dfrac{20}{7} \): \[ N = 70 \times \dfrac{20}{7} = 200 \] Find the number of students who are 10 years old: \[ \dfrac{1}{20} N = \dfrac{1}{20} \times 200 = 10 \] Thus, the number of students who are \( 10 \) years old is \( 10 \).

The area of the original square is: \[ A_1 = s^2 \]

If the side length is doubled, the new side length becomes \( 2s \), and the area of the new square is: \[ A_2 = (2s)^2 = 4s^2 \]

The ratio of the areas of the original square to the new square is: \[ \dfrac{A_1}{A_2} = \dfrac{s^2}{4s^2} = \dfrac{1}{4} \] So, the ratio of the areas is 1:4.

We are given that when a whole number \( N \) is divided by \( 13 \), it results in a quotient of \( 15 \) and a remainder of \( 2 \). Using the division algorithm: \[ N = \text{divisor} \times \text{quotient} + \text{remainder} \] Substituting the given values: \[ N = 13 \times 15 + 2 \] \[ N = 195 + 2 \] \[ N = 197 \] Thus, the required number is \( 197 \) .

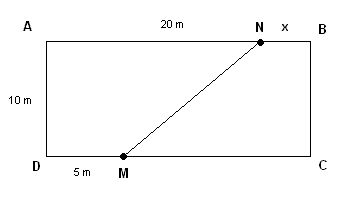Given the new information:

\( AN = 20 \)

\( AB = 20 + x \)

\( MC = 20 + x - 5 = 15 + x \)

Calculate the Total Area of Rectangle \( ABCD \) \[ \text{Area} = (\text{length}) \times (\text{width}) = AB \times AD = = (20 + x) \times 10 \] \[ = 200 + 10x \] Since quadrilateral \( MNBC \) has 40% of this area: \[ \text{Area of } MNBC = 0.4 \times (200 + 10x) = 80 + 4x \] Calculate the Area of trapezoid \( MNBC \) \[ \text{Area of trapezoid} MNBC = \dfrac{1}{2} \times \text{height} \times (NB + MC ) \] \[ = \dfrac{1}{2} \times 10 \times (x + 15 + x) \] \[ \text{Area of } MNBC = 0.4 \times (200 + 10x) = 80 + 4x \] Hence the equation \[ \dfrac{1}{2} \times 10 \times (x + 15 + x) = 80 + 4x \] Solving for \( x \): \[ 5 \times (2 x + 15) = 80 + 4x \] \[ x = \dfrac{5}{6} \; \text{m} \]

The person jogged for 30 minutes at a speed of \( 12 \) km/h \[ 30 \text{ min} = \dfrac{30}{60} = 0.5 \text{ hours} \]

Calculate the total distance jogged: \[ \text{Distance} = \text{Speed} \times \text{Time} = 12 \times 0.5 = 6 \text{ km} = 6000 \text{ m} \]

The jogger ran 10 laps around the field, so the perimeter of the field is: \[ \dfrac{6000}{10} = 600 \text{ m} \]

Let the width of the field be \( w \) meters. Since the length is twice the width, we have: \[ \text{Length} = 2w \]

The formula for the perimeter of a rectangle is: \[ 2(\text{Length} + \text{Width}) = 600 \]

Substituting \( \text{Length} = 2w \) and \( \text{Width} = w \) \[ 2(2w + w) = 600 \] \[ 6w = 600 \] \[ w = 100 \]

Since \( \text{Length} = 2w = 2(100) = 200 \), the area is: \[ \text{Area} = \text{Length} \times \text{Width} = 200 \times 100 = 20000 \text{ m}^2 \]

The area of the field is: \[ 20000 \text{ m}^2 \]

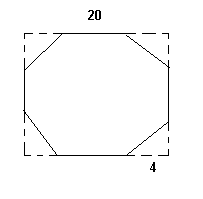
The area of the original square is: \[ A_{\text{square}} = 20 \times 20 = 400 \text{ square units} \]

Each triangle is an isosceles right triangle, so its area is given by: \[ A_{\text{triangle}} = \dfrac{1}{2} \times \text{leg} \times \text{leg} \] \[ = \dfrac{1}{2} \times 4 \times 4 = \dfrac{16}{2} = 8 \text{ square units} \] Since there are 4 such triangles: \[ A_{\text{total triangles}} = 4 \times 8 = 32 \text{ square units} \] The Area of the Remaining Octagon \[ A_{\text{octagon}} = A_{\text{square}} - A_{\text{total triangles}} \] \[ = 400 - 32 = 368 \text{ square units} \] Thus, the area of the remaining octagon is \( 368 \) square units.

Convert Kilometers to Meters. We know that: \[ 1 \text{ km} = 1000 \text{ m} \] So, \[ 75 \text{ km} = 75 \times 1000 = 75000 \text{ m} \] Convert Hours to Minutes. \[ 1 \text{ hour} = 60 \text{ minutes} \] Thus, the car's speed in meters per minute is: \[ \dfrac{75000 \text{ m}}{60 \text{ min}} = 1250 \; \text{meters per minute} \] The car travels \( 1,250 \; \text{meters per minute} \).

Let \( S \) be Linda's original savings.

She spent \( \dfrac{3}{4} \) of her savings on furniture.

The rest of her savings was spent on a TV, which cost $200.

The fraction of savings spent on the TV is \[ 1 - \dfrac{3}{4} = \dfrac{4}{4} - \dfrac{3}{4} = \dfrac{1}{4} \]. So, \( \dfrac{1}{4} \) of her original savings is equal to $200.

We can write this as an equation: \[ \dfrac{1}{4}S = 200 \] To find her original savings \( S \), we multiply both sides of the above equation by \( 4\): \[ 4 \times \dfrac{1}{4}S = 4 \times 200 \] Solve for \( S \) \[ S = 800 \] Therefore, Linda's original savings were \( \$ 800 \).

Original Cylinder: Radius \( r \) and height of water \( h_1 = 15 \) cm.

New Cylinder: Radius \( 2r \), and we need to find the new height \( h_2 \) after transferring the water.

The volume of a cylinder is given by: \[ V = \pi r^2 h \] For the original cylinder: \[ V_1 = \pi r^2 \times 15 \] Since the amount of water remains the same, the volume of water in the new cylinder is also \( V_1 \), but with a different radius \( 2r \): \[ V_2 = \pi (2r)^2 \times h_2 \] Since \( V_1 = V_2 \), we set up the equation: \[ \pi r^2 \times 15 = \pi (4r^2) \times h_2 \] Canceling \( \pi \) and \( r^2 \): \[ 15 = 4 h_2 \] Solve for \( h_2 \) \[ h_2 = \dfrac{15}{4} = 3.75 \text{ cm} \] Thus, the height of the water in the new container is \( 3.75 \) cm.

The original price of the sweater is \( P = \$ 30 \)

Stuart bought the sweater on sale for \( 30\% \) off the original price.

The discount amount is \( 30\% \) of \( P \), hence the discounted price after the first sale is \[ P - 0.30 P = \$ 30 - \$ 9 = \$ 21 \]. he received another \( 25\% \) off the discounted price.

The second discount amount is \[ 25\% \; \text{of} \; \$ 21 = 0.25 \times \$ 21 = \$ 5.25 \] The final price of the sweater is the discounted price minus the second discount: \[ \$ 21 - \$ 5.25 = \$ 15.75 \]. Therefore, the final price of the sweater was \( \$ 15.75 \).

Let the original price of the shirt be \( P \).

After the first discount, the price becomes: \[ P_{\text{after first discount}} = P - 0.25P = 0.75P \] The price after the second discount: \[ P_{\text{final}} = 0.75P - 0.25(0.75P) = 0.75P - 0.1875P = 0.5625P \] We are given that the final price is \( \$ 16 \), so: \[ 0.5625P = 16 \] Solve for \( P \). \[ P = \dfrac{16}{0.5625} \] The original price of the shirt before the first discount was approximately \( \$ 28.44 \).

To convert millimeters to inches, we use the conversion factor: \[ 1 \text{ mm} = 0.0393701 \text{ inches} \] Now, converting 2000 mm: \[ 2000 \times 0.0393701 = 78.74 \] So, \( 2000 \) millimeters is approximately \( 78.74 \) inches.

Let the Width of the rectangular playground be \( w \).

Since the Length is three times the width, the length is \( 3w \).

The area of a rectangle is given by: \[ \text{Area} = \text{Length} \times \text{Width} \] Substituting the given values: \[ 3w \times w = 75 \] Solve for \( w \) \[ 3 w^2 = 75 \] \[ w^2 = 25 \] \[ w = 5 \] So, the width is \( 5 \) meters, and the length is: \[ 3 \times 5 = 15 \text{ meters} \] The perimeter of a rectangle is given by: \[ P = 2(\text{Length} + \text{Width}) \] \[ P = 2(15 + 5) = 2(20) = 40 \text{ meters} \] The perimeter of the playground is \( 40 \) meters.

John sold books over five days: \[ 75 + 50 + 64 + 78 + 135 = 402 \] The Remaining Books (not sold) \[ 1200 - 402 = 798 \] The percentage of books not sold is: \[ \left( \dfrac{798}{1200} \right) \times 100 = 66.5\% \] So, \( 66.5 \% \) of the books were not sold.

We are given the equation: \[ N \times 0.75 = 1 \] Solve for \( N \) \[ N = \dfrac{1}{0.75} \] Since \( 0.75 = \dfrac{3}{4} \), we rewrite: \[ N = \dfrac{1}{\dfrac{3}{4}} = \dfrac{4}{3} \] We need to check which option equals \( \dfrac{4}{3} \):

A) \( 1 \dfrac{1}{2} = 1 + \dfrac{1}{2} = \dfrac{2}{2} + \dfrac{1}{2} = \dfrac{3}{2} \) Not equal to \( N \)

B) \( 1 \dfrac{1}{3} = 1 + \dfrac{1}{3} = \dfrac{3}{3} + \dfrac{1}{3} = \dfrac{4}{3} \) equal to \( N \)

C) \( \dfrac{5}{3} \) Not equal to \( N \)

D) \( \dfrac{3}{2} \) Not equal to \( N \) Final Answer: \[ \boxed{B} \]

Identify the significant figures: \( 6.76 \)

Count how many places the decimal moves to get from \( 6.76 \) to \( 6,760,000,000 \): \( 9 \) places

Write in scientific notation: \[ 6.76 \times 10^9 \] So, the 2008 world population in scientific notation is: \[ \mathbf{6.76 \times 10^9} \]