Grade 8 Math Practice Test

Online grade 8 math practice test questions are presented along with their detailed solutions.

    1 - Numbers

  1. Evaluate the following expressions.
    2. \[ a) \left[-2 \times (-4) + 3\right] \times \left[3 \times (-4) - 4\right] \] \[ b) \left[-2 \times (-3 + 1) + 3\right] \times \left[2 \times (-3 - 5) - 4\right] \]
  2. Which of the following is NOT a rational number?
    3. \[ a) \; (0.2) \qquad b) \; \pi \qquad c) \; \dfrac{2}{5} \]
  3. What is the value of the digit 5 in the number 34.6597?

    4. 2 - Sequences

  4. What is the next term in the sequence?
    5. \[ 3,,6,,9,,12,,\ldots \]
  5. What is the next term in the sequence?
    6. \[ 1,,3,,9,,27,,\ldots \]
  6. A sequence of numbers is defined by:
    7. \[ 2n + 1 \quad \text{for } n = 1,2,3,\ldots \]

    a) Find the first five terms of the sequence starting with \( n = 1 \).
    b) Is the given sequence arithmetic, geometric, or neither?

  7. A sequence of numbers is defined by:
    8. \[ 3 \times 2^{,n-1} \quad \text{for } n = 1,2,3,\ldots \]

    a) Find the first five terms of the sequence starting with \( n = 1 \).
    b) Is the given sequence arithmetic, geometric, or neither?

    3 - Sets

  8. Sets \( S_1 \) and \( S_2 \) are defined as follows:
    \( S_1 = \{0, 2, 9, 12\} \quad \) and \( \quad S_2 = \{2, 9, 10, 11, 12\} \)
    Find the elements of:
    a) \( S_1 \cap S_2 \)
    b) \( S_1 \cup S_2 \)
  9. Let the following sets be defined:
    \( Q = \text{All Rational Numbers} \) \( P = \text{All Irrational Numbers} \) \( R = \text{All Real Numbers} \)
    Which of the following is true?
    a) \( Q \cap P = R \quad \) b) \( Q \cup P = R \quad \) c) \( Q \cup P = \text{Empty Set} \quad \) d) \( Q \cap P = \text{Empty Set} \)

    10. 4 - Factors, Multiples and Divisibility

  10. Express the numbers as a product of prime factors:
    a) \(345 \quad \) b) \(150 \quad \) c) \(210\)
  11. What is the Greatest Common Factor (GCF) of \(100\) and \(180\)?
  12. What is the Least Common Multiple (LCM) of \(100\) and \(15\)?
  13. Which of the following numbers is divisible by \(3\)?
    a) \(101899 \quad \) b) \(900234 \quad \) c) \(134567280\)
  14. Which of the following numbers is divisible by \(4\)?
    a) \(189001 \quad \) b) \(1005612 \quad \) c) \(1003456024\)
  15. Which of the following numbers is divisible by \(6\)?
    a) \(234 \quad \) b) \(12345 \quad \) c) \(12114290910\)

    16. 5 - Fractions and Mixed Numbers

  16. Which pairs of fractions are equivalent?
    a) \( \dfrac{10}{15},\; \dfrac{7}{3} \quad \) b) \( \dfrac{8}{12},\; \dfrac{2}{3} \quad \) c) \( \dfrac{7}{12},\; \dfrac{21}{36} \)
  17. Evaluate:
    a) \( \dfrac{2}{5} + \dfrac{3}{10} - \dfrac{1}{15} \quad \) b) \( \dfrac{7}{16} \times \dfrac{4}{14} \quad \) c) \( \dfrac{11}{2} \div 4 \)
    d) \( 4\dfrac{3}{4} - 1\dfrac{1}{2} + 1\dfrac{1}{8} \quad \) e) \( 1\dfrac{3}{4} \div \left(3 + \dfrac{1}{3}\right) \)
  18. Write as fractions in reduced form:
    a) \(0.2 \div 0.6 \quad \) b) \(1 \div 0.4\)
  19. Dalia spends one quarter of her salary on food and beverages. She spends: - one fifth of that on soft drinks - one sixth of that on cookies
    What fraction of her salary is spent on soft drinks and cookies?
  20. James spends 2 hours/day on homework Mon–Fri. Ben spends \( \dfrac{3}{4} \) as much; Linda spends \( \dfrac{5}{4} \) as much.
    How many hours do they spend in a week?
  21. Sara made 1.5 L of juice. Her glasses hold \( \dfrac{1}{6} \) L.
    How many glasses can she fill?

    22. 6 - Exponents and Scientific Notation

  22. Evaluate:
    a) \( (-2)^3 - 5^3 + (-3)^4 \)
    b) \( (-1)^{-3} - 5^0 + \dfrac{4^2}{(-2)^4} \)
    c) \( \left(\dfrac{3}{4}\right)^2 + \left(\dfrac{4}{3}\right)^{-2} \)
  23. Write in exponential form (base ten):
    a) \(10000 \quad \) b) \(0.0000001 \quad \) c) \( \dfrac{1}{100000} \)
  24. Write in scientific notation:
    a) \(12.4 \times 10^3 \quad \) b) \(0.0023 \times 10^{-2} \quad \) c) \( \dfrac{12}{100000} \)

    25. 7 - Roots

  25. Simplify:
    a) \( \sqrt{16} \quad \) b) \( \sqrt{9} \quad \) c) \( \sqrt[3]{8} \)
  26. Reduce to simplest form:
    a) \( \sqrt{3 \times 25} \quad \) b) \( \sqrt{36 \times 5} \quad \) c) \( \sqrt[3]{8 \times 7} \)

    27. 8 - Proportionality

  27. Leila walked for 5 hours. The graph gives distance \(d\) vs. time \(t\).
    a) Write an equation \( d = k t \).
    b) If she started at 8 AM, when was she 10 km away?
  28. Does the table indicate that \(y\) is proportional to \(x\)?

    a) If yes, find \(k\) such that \( y = kx \).
    b) Find \(y\) for \(x=10.2\).
  29. A tap fills 10 L in 2 min, 20 L in 4 min, 30 L in 6 min.
    a) Plot points with \(V\) on vertical axis, \(t\) horizontal.
    b) Is \(V\) proportional to \(t\)?
    c) If yes, find \(k\) such that \(V = kt\).
    d) Find time to fill 100 L.

    30. 9 - Percent

  30. An item costs $120 and increases by 12%. What is the new price?
  31. Jimmy spends 50% of salary on rent + bills, and 15% of that amount on bills. What percent of salary is spent on bills?
  32. A meal costs $40. Tax is 15%; tip is 5% of the taxed amount. What is the total cost?
  33. Kamelea earns $5000 and spends: $400 on clothes, $1200 rent, $200 bills, $1200 food/outings, $600 car, rest saved.
    What percent is saved?
  34. \(10\%\) of one third of a number is 3. What is the number?
  35. Gas rose from $3→$4 per gallon in US and €1.5→€2 per liter in France. Which saw a larger percent increase?

    36. 10 - Unit Conversion

  36. Convert 10.5 ft to meters given \(1\,\text{m}=3.28084\,\text{ft}\).
  37. Convert 1.3 km to yards given \(1\,\text{km}=1093.61\,\text{yd}\).
  38. Convert \(1.2\,m^2\) to \(yd^2\) given \(1\,m=1.09361\,yd\).
  39. Convert \(100\,\text{km/hr}\) to m/s.

    40. 11 - Evaluate Expressions

  40. Evaluate \( \dfrac{1}{x+2} - \dfrac{1}{x-2} \) for \(x=1\).
  41. Evaluate \( \left|\dfrac{-x+1}{-6}\right| + x^2 - 1 \) for \(x=-5\).
  42. Evaluate \( 2^a - \sqrt{b^2} \) for \(a=2\), \(b=-2\).

    43. 12 - Algebra

    Review
    The distributive property: \[ a(x+y) = ax + ay \] Factoring: \[ ax + ay = a(x+y) \]

  43. Simplify:
    a) \(3(x+2) + x - 12 \quad \) b) \( \dfrac{1}{5}(15x+20) + 2x + 4 \quad \) c) \(0.2(5x+10) + 3x - 4\)
  44. Simplify:
    a) \(2x \cdot 3x \quad \) b) \( \dfrac{1}{2}x \cdot \dfrac{4}{5}x \quad \) c) \(3x^2 \cdot 5x^3\)
  45. Factor:
    a) \(21x + 7 \quad \) b) \(24 - 20x \quad \) c) \(8b - 4a + 32\)

    46. 13 - Equation with One Variable and Related Problems

  46. Solve the equations
    a) \(\; 3(x - 2 ) = 3 \quad\) b) \(\; 2(9 - x) = - (x + 5)\)

    c) \(\; \dfrac{x+1}{3} = 6 \quad\) d) \(\; 4\left(x + \dfrac{1}{4}\right) = -15 \quad\) e) \(\; x - \dfrac{x}{2} = 3\)

  47. A rectangular garden has a length of 12 meters and a width of 8 meters (diagram not to scale). A path of width \(x\) is constructed around the garden so that the outer perimeter is twice the original perimeter.
    Rectangular Garden with Path
    a) Write an equation in \(x\).
    b) Solve for \(x\).
    c) Find the length and width of the outer part.
    d) Find the total area (garden + path).
    e) Find the garden area.
    f) Find the area of the path.

  48. When 10 is subtracted from twice a number and the result is multiplied by one-half, the answer is 5. What is the original number?

    14 - Inequality with One Variable

  49. Solve the inequalities
    a) \(\; x + 2 < 4 \quad\) b) \(\; 2(x + 3) \ge 2 \quad\) c) \(\; -3x + 2 \le 11 \quad\) d) \(\; \dfrac{4x+1}{2} \ge x + 3\)

    15 - Functions

  50. Which of the following ordered pairs represents a function?
    a) \(\; \{ (1,2), (3,4), (5,7), (5,9) \} \quad\) b) \(\; \{ (-1,-2), (3,4), (5,7), (7,9) \} \quad\) c) \(\; \{ (3,3), (9,4), (5,7), (9,0) \}\)

  51. Which of the graphs below may be the graph of a linear function? Find its equation.
    Graph of Functions

  52. Given the function \(y = 2x + 1\),
    a) Find \(y\) for \(x = 0\) and \(x = 1\).
    b) Use these values to graph \(y = 2x + 1\).

  53. The graph of two functions is shown below.
    Graph of Linear Functions
    a) Without any calculations, which function has the higher rate of change?
    b) Find coordinates of two points on each graph.
    c) Use these points to find each rate of change.
    d) Compare the rates and confirm your answer to part (a).

    16 - Two-Dimensional Figures

  54. The legs of a right triangle are 6 cm and 8 cm. What is the length of the hypotenuse?

  55. In the figure below, three straight lines intersect at \(O\). Given \( \angle AOB = 31^\circ \) and \( \angle AOC = 79^\circ \), find \( \angle EOF \).
    Vertical Angles

  56. How many lines of symmetry does a square have?

  57. Use the figure below to find the measures of all eight angles \(\quad m\angle 1, m\angle 2, \ldots, m\angle 8 \quad\) given that \[ m\angle 1 = 40^\circ \]
    Parallel and Intersecting Lines

    17 - Perimeter and Area of Planar Figures

  58. Calculate the area of a circle with diameter \(20\) cm.
  59. Calculate the area of a right triangle with one leg of length \(16\) cm and hypotenuse \(20\) cm.
  60. In the figure below, ABDE is a square and FC is a line of symmetry of the blue arrow. Find the area of the arrow (shaded in blue).
    Area of Arrow
  61. Find the area of the blue-shaded shape bounded by a semicircle (diameter DE) and an isosceles triangle ABG. Round to two decimal places.
    Area of Compound Shape

    62. 18 - Volumes and Surface Area

  62. Find the volume and surface area (excluding the bottom) of a silo consisting of a cylinder of height \(h = 10\) m and a hemisphere of radius \(r = 6\) m on top.
    Cylinder and Half Sphere
  63. A rectangular prism is split by a diagonal plane (in red) into two congruent triangular prisms. Find the volume and surface area of one triangular prism obtained.
    Triangular Prism From Rectangular Prism

    19 - Data and Graphs

  64. The line plot below shows average high temperatures (°C) for 12 months in Ottawa, Canada.
    a) What is the average high temperature of the coldest month?
    b) What is the average high temperature of the hottest month?
    c) What is the temperature difference between the coldest and hottest months?
    d) What is the smallest increase between two consecutive months?
    e) What is the smallest decrease between two consecutive months?

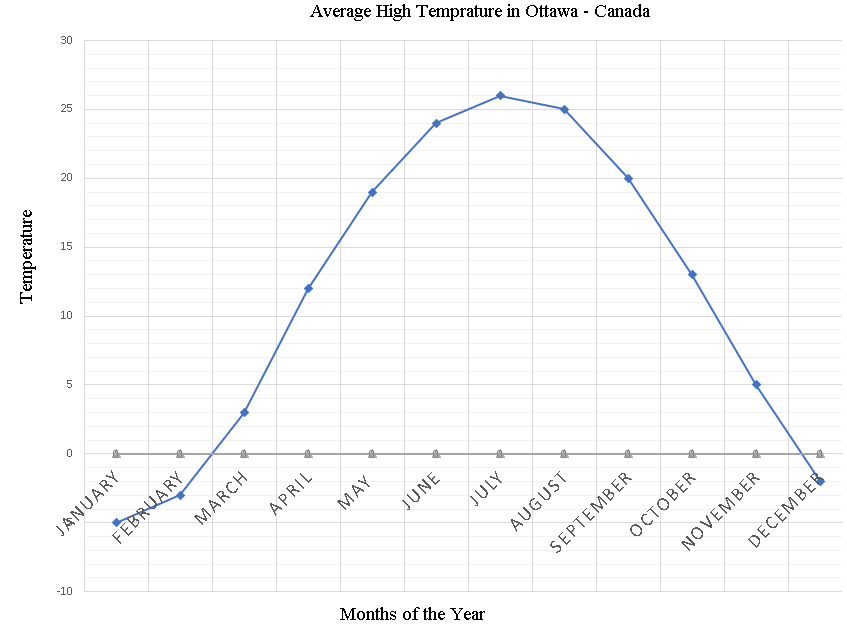
    Average High Temperature in Ottawa
  65. The scores of 25 students on a test are:
    \(31, 44, 54, 69, 45, 55, 91, 76, 76, 77, 78, 70, 79, 67, 60, 85, 84, 89, 56, 67, 86, 64, 97, 88, 92\)
    a) Order the data from smallest to largest.
    b) Find the range.
    c) Create a frequency table with classes starting at \(30–39\).
    d) Make a histogram.
    e) If scores below 60 are failing, what percent failed?

    20 - Statistics

  66. Find the median, lower quartile, and upper quartile of \(\{9, 4, 3, 2, 3, 0, 2, 3, 1, 9, 10\}\).

  67. Mark scored \(83, 94, 97, 93\) on his first four quizzes. What must he score on the fifth quiz to have an average of at least 90?

    21 - Probabilities

  68. Dalida rolls a fair six-sided die. What is the probability of getting an even number?

  69. Katya tosses a fair coin and rolls a fair six-sided die.
    a) Probability of a tail and a 4.
    b) Probability of a head and an odd number.

  70. Ben selects a card labeled 1–3 at random, replaces it, then draws again.
    a) Probability of selecting 3 twice.
    b) Probability of selecting the same number both times.

  71. Linda surveys students: 5 prefer blue, 6 prefer brown, out of 20. What is the probability the next student prefers neither blue nor brown?