Solution
If \(x\) is the number to find, its square is \(x^{2}\). \(x\) is equal to its square, hence: \[ x = x^{2} \] Solve the above equation by factoring. First, write it with the right side equal to zero: \[ x - x^{2} = 0 \] \[ x(1 - x) = 0 \] Solutions: \[ x = 0 \quad \text{and} \quad x = 1 \] Check answers:1) \(x = 0\), its square is \(0^{2} = 0\). Hence \(x\) and its square are equal.
2) \(x = 1\), its square is \(1^{2} = 1\). Hence \(x\) and its square are equal.
Solution
Let \(x\) be the number to find. Half its square is \[ \frac{1}{2} x^2 \] \(x\) is equal to half its square, hence: \[ x = \frac{1}{2} x^2 \] First, write with the right side equal to zero: \[ x - \frac{1}{2} x^2 = 0 \] Factor: \[ x \left( 1 - \frac{1}{2}x \right) = 0 \] Solutions: \[ x = 0 \quad \text{and} \quad x = 2 \] Check answers: 1) \(x = 0\), half its square is \[ \frac{1}{2} \cdot 0^2 = 0 \] Hence \(x\) and half its square are equal. 2) \(x = 2\), half its square is \[ \frac{1}{2} \cdot 2^2 = 2 \] Hence \(x\) and half its square are equal.Solution
If \(x\) is the number to find, then the quarter of its square is \[ \frac{1}{4} x^2 \] \(x\) is equal to the quarter of its square, hence: \[ x = \frac{1}{4} x^2 \] First, write the above equation with its right side equal to zero: \[ x - \frac{1}{4} x^2 = 0 \] Factor \(x\) out: \[ x \left( 1 - \frac{1}{4}x \right) = 0 \] Solutions: \[ x = 0 \quad \text{and} \quad x = 4 \] Check answers: 1) \(x = 0\), quarter of its square is \[ \frac{1}{4} \cdot 0^2 = 0 \] Hence \(x\) and the quarter of its square are equal. 2) \(x = 4\), quarter of its square is \[ \frac{1}{4} \cdot 4^2 = 4 \] Hence \(x\) and the quarter of its square are equal.Solution
The average speed is given by \[ \text{Average speed} = \frac{\text{total distance}}{\text{total time}} \] If \(x\) is the distance from A to B, then the total distance is \(2x\) (away and return). The total time \(T\) is equal to \[ t_1 = \frac{x}{40} \quad \text{(away)}, \quad t_2 = \frac{x}{60} \quad \text{(return)} \] Hence \[ T = \frac{x}{40} + \frac{x}{60} = \frac{100x}{2400} = \frac{x}{24} \] The average speed is therefore \[ \frac{2x}{x/24} = 48 \ \text{mph} \]Solution
Let \(x\) be the distance traveled to the city, then the time taken is \[ \frac{x}{60} \] and the time to return is \[ \frac{x}{50} \] The total time is 5 hours, so \[ \frac{x}{60} + \frac{x}{50} = 5 \] Solving for \(x\): \[ \frac{5x + 6x}{300} = 5 \] \[ \frac{11x}{300} = 5 \] \[ x = \frac{1500}{11} \approx 136 \ \text{miles} \]Solution
Let \(t\) be the number of hours from 11:00 a.m. when Jimmy catches up with John. Jimmy will drive for \(t - \frac14\) hours (starting later). When they meet, the distances are equal: \[ 50t = 65\left(t - \frac14\right) \] Solving: \[ 50t = 65t - \frac{65}{4} \] \[ 15t = \frac{65}{4} \] \[ t = \frac{65}{60} \approx 1.083 \ \text{hours} \] That is \(1\) hour and \(5\) minutes after 11:00 a.m., so Jimmy catches up at \[ 12{:}05 \ \text{p.m.} \]Solution
First, find the slope of the line \(5x - 3y = 4\): \[ -3y = -5x + 4 \] \[ y = \frac{5}{3}x - \frac{4}{3} \] The slope is: \[ m_{\text{given}} = \frac{5}{3} \] Let \(m\) be the slope of the perpendicular line: \[ m \cdot \frac{5}{3} = -1 \] \[ m = -\frac{3}{5} \] The equation of the line containing \((-4, 5)\) and perpendicular to \(5x - 3y = 4\) is: \[ y - 5 = -\frac{3}{5}(x - (-4)) \] \[ y = -\frac{3}{5}x + \frac{13}{5} \] \[ 5y + 3x = 13 \]Solution
Let \(L\) and \(W\) be the length and width of the rectangle. We have: \[ L \cdot W = 300 \] \[ 2(L + W) = 80 \quad \Rightarrow \quad L + W = 40 \] From \(L + W = 40\): \[ W = 40 - L \] Substitute into \(L \cdot W = 300\): \[ L(40 - L) = 300 \] Standard form: \[ L^2 - 40L + 300 = 0 \] \[ (L - 30)(L - 10) = 0 \] Thus: \[ L = 30 \quad \Rightarrow \quad W = 10 \] \[ L = 10 \quad \Rightarrow \quad W = 30 \] Assuming \(L > W\), the rectangle has: \[ L = 30\ \text{m}, \quad W = 10\ \text{m} \]Solution
The area \(A\) of a trapezoid is: \[ A = \frac{1}{2} \cdot h \cdot (b_1 + b_2) \] Here \(b_1 = 12\ \text{cm}\), \(b_2 = 23\ \text{cm}\), but \(h\) (height) is not given. Therefore, there is not enough information to find the area.Solution
Let \(x\) be the side of the swimming pool. The area of the swimming pool is \(x^2\). Since the remaining area is half of the garden's area: \[ x^2 = \frac{1}{2} \cdot (100 \cdot 50) = 2500 \] Thus: \[ x = 50\ \text{m} \]

Solution
Note that since \(ABC\) is an equilateral triangle and \(BH\) is perpendicular to \(AC\), \[ HC = \frac{50}{2} = 25 \ \text{cm}. \] Also, since \(MN\) and \(HC\) are parallel, the two triangles \(BMN\) and \(BHC\) are similar and the sizes of their sides are proportional. Hence \[ \frac{BN}{BC} = \frac{MN}{HC} = \frac{BM}{BH} = \frac{12}{25}. \] The area of triangle \(BMN\) is given by \[ A = \frac12 \cdot BM \cdot MN. \] The area of triangle \(BHC\) is given by \[ B = \frac12 \cdot BH \cdot HC. \] Note the ratio of the two areas: \[ \frac{A}{B} = \frac{\frac12 BM \cdot MN}{\frac12 BH \cdot HC} = \frac{BM}{BH} \cdot \frac{MN}{HC} = \frac{12}{25} \cdot \frac{12}{25} = \left( \frac{12}{25} \right)^2. \] Let us now find \(BH\) using Pythagoras' theorem: \[ BH = \sqrt{50^2 - 25^2} = 25\sqrt{3}. \] The area \(B\) of triangle \(BHC\) is given by: \[ B = \frac12 \cdot 25\sqrt{3} \cdot 25 = \frac12 \cdot 25^2 \sqrt{3}. \] We now use the ratio \(\frac{A}{B} = \left(\frac{12}{25}\right)^2\) to find \(A\), the area of triangle \(BMN\): \[ A = \left(\frac{12}{25}\right)^2 \cdot B = \left(\frac{12}{25}\right)^2 \cdot \frac12 \cdot 25^2 \sqrt{3} = 72\sqrt{3} \ \text{cm}^2. \]

Solution
We first find the volume of water without the stone: \[ V_1 = 10 \cdot (\pi \cdot 5^2) = 250\pi \quad (\pi \approx 3.14). \] The volume of water and stone is given by: \[ V_2 = 13.2 \cdot (\pi \cdot 5^2) = 330\pi. \] The volume of the stone is: \[ V_2 - V_1 = 330\pi - 250\pi = 80\pi \approx 251.1 \ \text{cm}^3. \]

Solution
The size of the diagonal of the square is equal to the diameter of the circle. The side \(x\) of the square is such that \[ x^2 = 400 \quad \Rightarrow \quad x = 20 \ \text{cm}. \] The diagonal \(D\) of the square is found using Pythagoras' theorem: \[ D^2 = x^2 + x^2 = 800 \quad \Rightarrow \quad D = \sqrt{800}. \] The area \(A\) of the circle is: \[ A = \pi \left(\frac{D}{2}\right)^2 = \frac{\pi D^2}{4} = 200\pi \approx 628 \ \text{cm}^2. \]Solution
The average of \(2, 3, 5, x\) is: \[ \frac{2 + 3 + 5 + x}{4}. \] It is known to be equal to 4, hence: \[ \frac{2 + 3 + 5 + x}{4} = 4. \] Solving for \(x\): \[ 10 + x = 16 \quad \Rightarrow \quad x = 6. \]Solution
The average of \(x, y, z, w\) is equal to 25. Hence \[ \frac{x + y + z + w}{4} = 25 \] The average of \(x, y, z\) is equal to 27. Hence \[ \frac{x + y + z}{3} = 27 \] This gives \[ x + y + z = 3 \times 27 = 81 \] Substitute \(x + y + z = 81\) into \(\frac{x + y + z + w}{4} = 25\): \[ \frac{81 + w}{4} = 25 \] Solving for \(w\): \[ w = 19 \]Solution
The arithmetic mean of \(41, 46, x, y, z\) is 50. Hence \[ \frac{41 + 46 + x + y + z}{5} = 50 \] Rearranging: \[ x + y + z = 163 \] The mode is the repeated value. We cannot have \(x = y = z = 45\) because their sum would not be 163. The only possibility is \(x = y = 45\). Thus: \[ 45 + 45 + z = 163 \] Solving: \[ z = 73 \]Solution
Substitute \(x = 2\) into the equation: \[ 2(2) + 1 = 2A + 3(2 + A) \] Solving for \(A\): \[ A = -\frac{1}{5} \]Solution
Since \(1\ \text{dm} = 10\ \text{cm}\), we convert: \[ r = 50\ \text{cm} = 5\ \text{dm}, \quad h = 1\ \text{m} = 10\ \text{dm} \] The volume of the cylinder is: \[ V = \pi r^2 h = 3.14 \times (5\ \text{dm})^2 \times 10\ \text{dm} = 785\ \text{dm}^3 \] Since \(1\ \text{dm}^3\) weighs \(1\ \text{kg}\), the total weight is: \[ 785\ \text{dm}^3 \times \frac{1\ \text{kg}}{\text{dm}^3} = 785\ \text{kg} \]
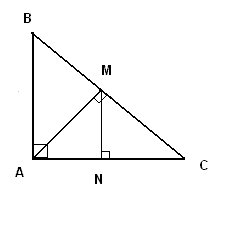
Solution
Since \(ABC\) is isosceles: \[ AB = AC \] Triangles \(ABM\) and \(ACM\) have equal sides, one common side, and equal angles, so they are congruent. Hence the area of triangle \(AMC\) is half that of \(ABC\). In triangle \(MAC\), angles \(\angle MAC\) and \(\angle MCA\) are each \(45^\circ\), so triangle \(MAC\) is isosceles right. Thus, triangles \(MAN\) and \(MCN\) are congruent. The area of triangle \(MNC\) is half the area of triangle \(AMC\). Therefore, \[ \frac{\text{Area of } MNC}{\text{Area of } ABC} = \frac{1}{4} \]Pump A can fill a tank of water in 4 hours. Pump B can fill the same tank in 6 hours. Both pumps are started at 8:00 a.m. to fill the same empty tank. An hour later, pump B breaks down and took one hour to repair and was restarted again. When will the tank be full? (round your answer to the nearest minute).
Solution
Pump A can fill 1 tank in 4 hours; hence the rate of pump A is
\[ \frac{1}{4} \ \text{(tank/hour)} \]Pump B can fill 1 tank in 6 hours; hence the rate of pump B is
\[ \frac{1}{6} \ \text{(tank/hour)} \]Let \( t \) be the number of hours it takes Pump A to fill the tank. During \( t \) hours Pump A fills
\[ t \times \frac{1}{4} \]Pump B was stopped for one hour and hence will pump water into the tank for \( t - 1 \) hours; hence during \( t - 1 \) hours Pump B fills
\[ (t - 1) \times \frac{1}{6} \]The two pumps work together to fill 1 tank; hence
\[ t \times \frac{1}{4} + (t - 1) \times \frac{1}{6} = 1 \]Multiply through by 24 and simplify:
\[ 6t + 4(t - 1) = 24 \] \[ 10t = 28 \] \[ t = 2.8 \ \text{hours} = 2 \ \text{hours} + 0.8 \times 60 \ \text{minutes} = 2 \ \text{hours} \ 48 \ \text{minutes} \]The tank is full at
\[ 8{:}00 \ \text{a.m.} + 2 \ \text{hours} \ 48 \ \text{minutes} = 10{:}48 \ \text{a.m.} \]Are the lines with equations \( 2x + y = 2 \) and \( x - 2y = 0 \) parallel, perpendicular or neither?
Solution
Write each of the given equations in the form \( y = m x + b \) and identify the slope \( m \).
From \( 2x + y = 2 \): \[ y = -2x + 2, \quad m_{1} = -2 \] From \( x - 2y = 0 \): \[ y = \frac{x}{2}, \quad m_{2} = \frac{1}{2} \]\( m_{1} \) and \( m_{2} \) are not equal and therefore the lines are not parallel. The product of the two slopes is
\[ m_{1} \times m_{2} = (-2) \times \frac{1}{2} = -1 \]The two lines are perpendicular.
What are the dimensions of the square that has the perimeter and the area equal in value?
Solution
Let \( x \) be the side of the square. The perimeter \( 4x \) and the area \( x^{2} \) are equal; hence
\[ 4x = x^{2} \]Solve the above equation:
\[ x^{2} - 4x = 0 \] \[ x(4 - x) = 0 \]Two solutions:
\[ x = 0 \quad\text{(square does not exist)} \] \[ x = 4 \quad\text{(square of side 4 units)} \]Find the dimensions of the rectangle that has a length 3 meters more than its width and a perimeter equal in value to its area.
Solution
Let \( L \) be the length and \( W \) be the width. "A length 3 meters more than its width" is written as
\[ L = W + 3 \]The perimeter of the rectangle is
\[ 2L + 2W \]The area of the rectangle is
\[ LW \]"Perimeter equal in value to its area" is written as
\[ 2L + 2W = LW \]Substitute \( L = W + 3 \) into the above equation:
\[ 2(W + 3) + 2W = (W + 3)W \] \[ 4W + 6 = W^{2} + 3W \] \[ W^{2} - W - 6 = 0 \]Solve the quadratic equation:
\[ W = 3 \quad\text{or}\quad W = -2 \]The width is positive, so \( W = 3 \) and
\[ L = W + 3 = 6 \]Find the circumference of a circular disk whose area is \(100\pi\) square centimeters.
Solution
The area is given by:
\[ A = \pi R^2 = 100 \pi, \quad \text{where } R \text{ is the radius.} \]Solving for \(R\):
\[ R^2 = 100 \quad\Rightarrow\quad R = 10 \ \text{cm} \]The circumference \(C\) is given by:
\[ C = 2 \pi R = 20 \pi \ \text{cm} \]The semicircle of area \(50 \pi\) square centimeters is inscribed inside a rectangle. The diameter of the semicircle coincides with the length of the rectangle. Find the area of the rectangle.
Solution
For a semicircle of radius \(R\), the area is:
\[ \frac{1}{2} \pi R^2 = 50 \pi \]Solving for \(R\):
\[ R^2 = 100 \quad\Rightarrow\quad R = 10 \]The length \(L\) of the rectangle equals the diameter of the semicircle:
\[ L = 2R = 20 \ \text{cm} \]The width \(W\) of the rectangle equals the radius of the semicircle:
\[ W = R = 10 \ \text{cm} \]The area of the rectangle is:
\[ \text{Area} = L \times W = 20 \times 10 = 200 \ \text{cm}^2 \]A triangle has an area of \(200 \ \text{cm}^2\). Two sides of this triangle measure 26 and 40 cm respectively. Find the exact value of the third side.
Solution
The area \(A\) of a triangle given two sides \(a\) and \(b\) with included angle \(\alpha\) is:
\[ A = \frac{1}{2} a b \sin \alpha \]Using the cosine rule to find \(\cos \alpha\):
\[ \cos \alpha = \frac{a^2 + b^2 - c^2}{2ab}, \quad c \text{ is the third side.} \]Using \(\sin \alpha = \sqrt{1 - \cos^2 \alpha}\), the area formula becomes:
\[ A = \frac{1}{2} a b \sqrt{1 - \left(\frac{a^2 + b^2 - c^2}{2ab}\right)^2} \]Simplifying:
\[ A = \frac{1}{4} \sqrt{4 a^2 b^2 - (a^2 + b^2 - c^2)^2} \]Solving for \(c\):
\[ c = \sqrt{a^2 + b^2 \pm \sqrt{4 a^2 b^2 - 16 A^2}} \]Substitute \(a = 26, b = 40, A = 200\):
\[ c_1 = \sqrt{356} = 2\sqrt{89}, \quad c_2 = \sqrt{4196} = 2\sqrt{1049} \]