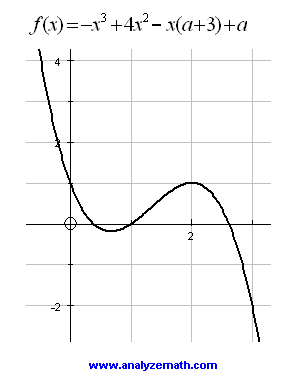Graphs of Third-Degree Polynomials

The graphs of several third-degree polynomials are shown below, along with questions and answers at the bottom of the page.

Polynomial of third degree: cuts the x-axis at one point.
Question 1: Why does the graph cut the x-axis at one point only?

Figure 1: Graph of the third-degree polynomial.
Polynomial of third degree: 3 x-intercepts.
Question 2: If the graph cuts the x-axis at \(x = -2\), what are the coordinates of the two other x-intercepts?

Figure 2: Graph of a third-degree polynomial with 3 x-intercepts.
Polynomial of third degree: 3 x-intercepts with a parameter \(a\) to determine.
Question 3: The graph below cuts the x-axis at \(x = 1\) and has a y-intercept at \(y = 1\). What are the coordinates of the two other x-intercepts?

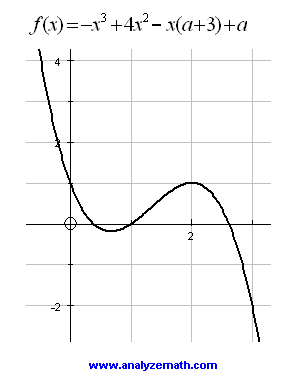
Figure 3: Graph of a third-degree polynomial with one parameter to determine.
Polynomial of third degree: one x-intercept.
Question 4: The graph below cuts the x-axis at \(x = -1\). Why does the graph of this polynomial have only one x-intercept?

Figure 4: Graph of a third-degree polynomial with one x-intercept.

Answers to Above Questions

Since \(x = 0\) is a repeated zero of multiplicity 3, the graph cuts the x-axis at only one point.
An x-intercept at \(x = -2\) implies \(x + 2\) is a factor of the polynomial. Hence, the polynomial can be written as: \[ f(x) = (x + 2)(x^2 + 3x + 1) \] The other zeros are found by solving \[ x^2 + 3x + 1 = 0 \] which gives \[ x = -\frac{3}{2} + \frac{\sqrt{5}}{2}, \quad x = -\frac{3}{2} - \frac{\sqrt{5}}{2}. \]
Use the y-intercept to find \(a = 1\). Then, similarly to Question 2, write \[ f(x) = a(x-1)(x^2 - 3x + 1) \] Solving \(x^2 - 3x + 1 = 0\) gives the other two x-intercepts: \[ x = \frac{3}{2} - \frac{\sqrt{5}}{2}, \quad x = \frac{3}{2} + \frac{\sqrt{5}}{2}. \]
Factor the polynomial as \[ f(x) = (x + 1)(x^2 + x + 1). \] Solving \[ x^2 + x + 1 = 0 \] yields complex zeros, which do not appear as x-intercepts. Therefore, there is only one real x-intercept at \(x = -1\).