Exemplo 1: Quantos números de 3 dígitos você consegue formar usando os dígitos 1, 2 e 3 sem repetições?
método (1) listando todos os números possíveis usando um diagrama de árvore.
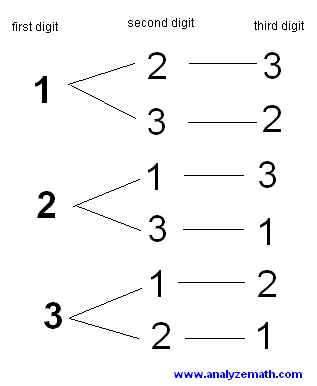
Podemos fazer 6 números usando 3 algarismos e sem repetições dos algarismos.
método (2) contagem:
OLHE O DIAGRAMA DE ÁRVORE ACIMA.
Temos 3 opções para o primeiro dígito, 2 opções para o segundo dígito e 1 escolha para o terceiro dígito.
Usando o princípio da contagem, podemos dizer:
O número total de números de 3 dígitos é dado por
3 × 2 × 1 = 6
Existe uma notação especial para o produto
3 × 2 × 1 = 3!
e é lido 3 fatorial.
Em geral n! é lido n fatorial e é dado por
\[ n! = n \times (n - 1) \times (n - 2) \times ... \times 2 \times 1 \]
Também definimos 0! = 1.
Exemplo 2: Quantas palavras diferentes podemos formar usando as letras A, B, E e L sem repetir as letras?
Solução: Temos 4 opções para a primeira letra, 3 opções para a segunda letra, 2 opções para a terceira letra e 1 escolha para a quarta letra. Portanto, o número de palavras é dado por
4 × 3 × 2 × 1 = 4! = 24
Permutações
Exemplo 3: Quantos números de 2 dígitos você pode formar usando os dígitos 1, 2, 3 e 4 sem repetir os dígitos?
Desta vez, queremos usar 2 dígitos de cada vez para formar números de 2 dígitos.
Para o primeiro dígito, temos 4 opções e para o segundo dígito, temos 3 opções (4 - 1 já usado). Usando o princípio da contagem, o número de números de 2 algarismos que podemos formar usando 4 algarismos é dado por
4 × 3 = 12
O problema acima é organizar 2 dígitos de 4 em uma ordem específica. Isso também é chamado de permutação.
A ideia mais importante nas permutações é que a ordem é importante. Quando você usa os dígitos 3 e 4 para formar um número, os números 34 e 43 são diferentes, portanto, a ordem dos dígitos 3 e 4 é importante.
Em geral, permutar r (2 dígitos no exemplo acima) itens de um conjunto de n (4 dígitos no exemplo acima) itens é escrito como \( _{n}P_{r} \) e a fórmula é dada por
\[ _{n}P_{r} = \dfrac{n!}{(n - r)!} \]
Exemplo 4: Calcular
\( _{4}P_{2} \)
\( _{6}P_{5} \)
\( _{4}P_{4} \)
Solução:
\( _{4}P_{2} = \dfrac{4!}{(4 - 2)!} = 24/2 = 12 \)
\( _{6}P_{5} = \dfrac{6!}{(6 - 5)}! = (6\times 5 \times 4 \times 3 \times 2 \times 1) / 1! = 720 \)
\( _{4}P_{4} = \dfrac{ 4! }{ (4 - 4)! } = 4! / 0! = 4! / 1 = 4 \times 3 \times 2 \times 1 = 24 \) (Agora entendemos a necessidade de definir 0! = 1)
Exemplo 5: Quantas palavras de 3 letras podemos formar com as letras da palavra LOVE?
Solução: Existem 4 letras na palavra amor e formar palavras de 3 letras é semelhante a organizar essas 3 letras e a ordem é importante, pois LOV e VOL são palavras diferentes devido à ordem das mesmas letras L, O e V. Portanto, é um problema de permutação. O número de palavras é dado por
\( _{4}P_{3} = \dfrac{4!}{(4 - 3)!} = \dfrac{4!}{1!} = 24 \)
Combinações
Exemplo 6: Quantas linhas você pode desenhar usando 3 pontos não colineares (não em uma única linha) A, B e C em um plano?
Solução:
Você precisa de dois pontos para desenhar uma linha. A ordem não é importante. A linha AB é igual à linha BA. O problema é selecionar 2 pontos de 3 para desenhar linhas diferentes. Se procedermos como fizemos com as permutações, obteremos os seguintes pares de pontos para desenhar linhas.
AB , AC
BA , BC
CA , CB
Há um problema: a linha AB é igual à linha BA, o mesmo para as linhas AC e CA e BC e CB.
As retas são: AB, BC e AC; 3 linhas apenas.
Então na verdade podemos traçar 3 retas e não 6 e isso porque neste problema a ordem dos pontos A, B e C não é importante.
Este é um problema de combinação: combinar 2 itens de 3 e é escrito da seguinte forma:
\[ _{n}C_{r} = \dfrac{n!}{(n - r)! \; r!} \]
O número de combinações é igual ao número de permutações dividido por r! eliminar aqueles contados mais de uma vez porque a ordem não é importante.
Exemplo 7: Calcular
a) \( _{3}C_{2} \)
b) \( _{5}C_{5} \)
Solution:
Use a fórmula fornecida acima para as combinações
a)
\( _{3}C_{2} = \dfrac{3!}{ (3 - 2)!2! } = \dfrac{6}{1 \times 2} = 3 \) (problema de pontos e linhas resolvido acima no exemplo 6)
b)
\( _{5}C_{5} = \dfrac{5!}{(5 - 5)! \; 5!} = \dfrac{5!}{0! \; 5!} = \dfrac{ 5! }{1 * 5!} = 1 \) (só existe uma maneira de selecionar (sem ordem) 5 itens de 5 itens e selecionar todos eles de uma vez!)
Exemplo 8:Precisamos formar uma equipe de 5 em uma turma de 12 alunos. Quantas equipes diferentes podem ser formadas?
Solução:
Não há nada que indique que a ordem em que os membros da equipe são selecionados seja importante e, portanto, seja um problema de combinação. Portanto, o número de equipes é dado por
\( _{12}C_{5} = \dfrac{12!}{(12 - 5)! \; 5!} = 792 \)
Problemas com soluções
Quantos números de 4 algarismos podemos formar usando os algarismos 3, 6, 7 e 8 sem repetições?
Quantos números de 3 algarismos podemos formar usando os algarismos 2, 3, 4, 5 e 6 sem repetições?
Quantas palavras de 6 letras podemos formar usando as letras da palavra LIBERDADE sem repetições?
De quantas maneiras você pode organizar 5 livros diferentes em uma estante?
De quantas maneiras você pode selecionar um comitê de 3 alunos entre 10 alunos?
Quantos triângulos você pode fazer usando 6 pontos não colineares em um plano?
Um comitê incluindo 3 meninos e 4 meninas será formado a partir de um grupo de 10 meninos e 12 meninas. Quantos comitês diferentes podem ser formados a partir do grupo?
Em um determinado país, a placa do carro é formada por 4 dígitos dos dígitos 1, 2, 3, 4, 5, 6, 7, 8 e 9 seguidos por 3 letras do alfabeto. Quantas placas de matrícula podem ser formadas se nem os dígitos nem as letras se repetem?
