Algebra Questions to Practice for the EmSAT
\( \) \( \) \( \) \( \)
What is the solution set to the equation \( 4 = -(x +2)(x-1) \)?
- \( \left\{-\frac{1}{2}-i\dfrac{\sqrt{7}}{2} \quad , \quad \frac{1}{2}+i\dfrac{\sqrt{7}}{2} \right\} \)
- \( \{-2 , 1\} \)
- \( \left\{\frac{1}{2}-i\dfrac{\sqrt{7}}{2} \quad , \quad \frac{1}{2}+i\dfrac{\sqrt{7}}{2} \right\} \)
- \( \left\{-\frac{1}{2}-i\dfrac{\sqrt{7}}{2} \quad , \quad -\frac{1}{2}+i\dfrac{\sqrt{7}}{2} \right\} \)
Find all solutions to the equation \( 9^{-x\left(-x+5\right)}\:= \dfrac{1}{3^{-12}} \).
- \( \{6,2\} \)
- \( \{-1 , -2\} \)
- \( \{-1 , 6\} \)
- \( \{6,1\} \)
Write the expression \( \dfrac{1}{3 + \sqrt{-4}} \) as a complex number of the form \( a + i b \).
- \( \dfrac{3}{13}- i \dfrac{2}{13} \)
- \( \dfrac{1}{3}- i \dfrac{1}{2} \)
- \( \dfrac{3}{13} + i \dfrac{2}{13} \)
- \( \dfrac{1}{3} + i \dfrac{1}{2} \)
The graph the complex number \( -2(4 - i) \) is in quadrant
- \( I \)
- \( III \)
- \( IV \)
- \( II \)
Ahmed rented a car for two days and he paid a total of 261 AED. He was charged a fixed fee of 80 AED per day plus 20 fils for every kilometer traveled.
What is the total distance traveled?
(Give your answer to the nearest kilometer)
- \( 250 \) kilometers
- \( 505 \) kilometers
- \( 1305 \) kilometers
- \( 905 \) kilometers
Solve for \( x \) and \( y \) the following system of equations.
\[
\begin{cases}
\dfrac{x}{2}+\dfrac{y}{2}=1\\\\
\dfrac{x}{3}+\dfrac{y}{4}=2
\end{cases}
\]
- \( (3 , -2) \)
- \( (-18,-16) \)
- \( (18,-16)\)
- \( (-16,18) \)
Simplify.
\(
\dfrac{x^2 - 4y^2}{2y - x}
\)
Simplify the expression \( \sqrt{200} + \sqrt{32} \).
- \( 2 \sqrt{58} \)
- \( 14 \sqrt{2} \)
- \( 6 \sqrt{2} \)
- \( 2 \sqrt{14} \)
We suppose that the point with coordinates \( (a , - 3) \) is on the graph of the curve \( y = x(x-2) \). Find the constant \( a \) if possible.
- \( a = 3 \)
- \( a = 1 \)
- No real value of \( a \), which satisfies the above conditions, exists.
- \( a = -3 \)
The solution set of the equation \( \log_4(x) - \log_4(x+10) = -\log_4(x-2)\) is
- \( \{-2,5\} \)
- \( \{-2\} \)
- \( \{2,5\} \)
- \( \{5\} \)
Find all the solutions of the equation \( 2 - \dfrac{1}{x(x+1)} = \dfrac{3}{x+1} \).
- \( \{-1/2\} \)
- \( \{1\} \)
- \( \{-1/2,1\} \)
- \( \{1/2 , - 1\} \)
Find \( f^{-1}(-2) \) if \( f(x) = \sqrt{x + 2} - 4 \).
- \( 2 \)
- \( -2 \)
- \( -4 \)
- \( 0 \)
Which of the following is equivalent to the expression \( \sin(4x) \) for all values of \( x \)?
- \( 4 \sin(x) \)
- \( 4 \sin(x) \cos (x) \cos(2x) \)
- \( 2 \sin(2x) \)
- \( \sin(x) + 4 \)
What is the magnitude of vector \( \overrightarrow v \) given by \( \overrightarrow v = 2 \overrightarrow{v_1} - 3 \overrightarrow {v_2} \) where \( \overrightarrow{v_1} = <1,-2> \) and \( \overrightarrow{v_2} = <-2,4> \)?
- \( 2 \sqrt {6} \)
- \( 8 \)
- \( 8 \sqrt {5} \)
- \( 6 \)
A factory produced 2000 toys two years ago and 2400 toys this year. If we assume that the production varies linearly with the time, what will be the production of the factory in four years?
- \( 3200 \) toys
- \( 2800 \) toys
- \( 2600 \) toys
- \( 3000 \) toys
Find the solution set of the inequality \( \quad x + 4 \le \dfrac{3}{x+2} \).
- \( (-\infty ,-5] \)
- \( (-\infty ,-5] \cup (-2,-1) \)
- \( (-\infty ,-5] \cup (-2,-1] \)
- \( (-\infty ,-5) \cup (-2,-1] \)
Simplify: \( (-x+2)(x-1) - ( x^2 - 2x +1) \)
- \( -2x^2+x-1 \)
- \( -2x^2 - x-1 \)
- \( 2x^2+5x-3 \)
- \( -2x^2+5x-3 \)
Factor \( 3x^2 + 4x - 4 \) completely.
Find two positive real numbers such that their difference is \( 2 \) and their product is \( 99 \).
Solve the equation \( \quad x y = \dfrac{y - 1}{x - 1} \) for \( y \).
The sum of three real numbers \( x , y \) and \( z \) is equal to 96. The sum of \( y \) and \( z \) is equal to \( 74 \) and the difference \( z - y \) is equal to \( 12 \). Find the three numbers.
Which of the following equation could be the equation to the third degree polynomial \( P \) whose graph is shown below?
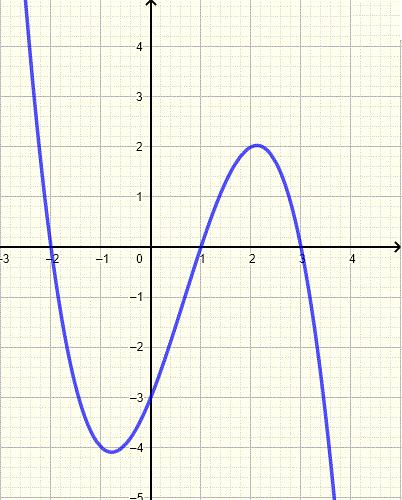
- \( P(x) = (x-2) (x+1) (x+3) \)
- \( P(x) = -0.5 (x+2) (x-1) (x-3) \)
- \( P(x) = 0.5 (x-2) (x+1) (x+3) \)
- \( P(x) = -0.5 (x-2) (x+1) (x-3) \)
Let \( f(x) = x^2 - 1 \) and \( g(x) = \dfrac{1}{x-2} \); find \( (f_o g)(0) \).
- \( -\dfrac{3}{4} \)
- \( -1 \)
- \( -\dfrac{1}{2} \)
- \( 0 \)
Mansour drank a cup of coffee with 120 milligrams of caffeine at 8:00 am. After five hours, the caffeine in Mansour's body decreased exponentially to half the initial amount. How much caffeine is left in Mansour's body at 6:00 pm?
- \( 60 \) milligrams
- \( 15 \) milligrams
- \( 45 \) milligrams
- \( 30 \) milligrams
Write the system of equations
\(
\begin{cases}
-2x + y - z = 1\\\\
5x - y = -3\\\\
-2x + 2z - 4 y = 0
\end{cases}
\)
in matrix form.
-
\(
\begin{bmatrix}
-2 & 1 & -1 \\
5 & -1 & 1 \\
-2 & - 4 & 2
\end{bmatrix}
\cdot
\begin{bmatrix}
x\\
y\\
z
\end{bmatrix}
=
\begin{bmatrix}
1 \\
-3 \\
0
\end{bmatrix}
\)
-
\(
\begin{bmatrix}
-2 & 1 & -1 \\
5 & -1 & 0 \\
-2 & - 4 & 2
\end{bmatrix}
\cdot
\begin{bmatrix}
x\\
y\\
z
\end{bmatrix}
=
\begin{bmatrix}
1 \\
-3 \\
0
\end{bmatrix}
\)
-
\(
\begin{bmatrix}
-2 & 1 & -1 \\
5 & -1 & 0 \\
-2 & 2 & -4
\end{bmatrix}
\cdot
\begin{bmatrix}
x\\
y\\
z
\end{bmatrix}
=
\begin{bmatrix}
1 \\
-3 \\
0
\end{bmatrix}
\)
-
\(
\begin{bmatrix}
-2 & 1 & -1 \\
5 & -1 & 0 \\
-2 & - 4 & 2
\end{bmatrix}
\cdot
\begin{bmatrix}
x\\
y\\
z
\end{bmatrix}
=
\begin{bmatrix}
1 \\
-3 \\
0
\end{bmatrix}
\)
Geometry Questions to Practice for the EmSAT
The circle with equation \( \quad 2(x - 2)^2 + 2(y + 2 )^2 = 32 \) has
- a center at \( (-2,2) \) and a radius \( r = 4 \)
- a center at \( (2,-2) \) and a radius \( r = 16 \)
- a center at \( (2,-2) \) and a radius \( r = 4 \)
- a center at \( (-2,2) \) and a radius \( r = 4 \)
Find \( x \) in the right triangle shown below.
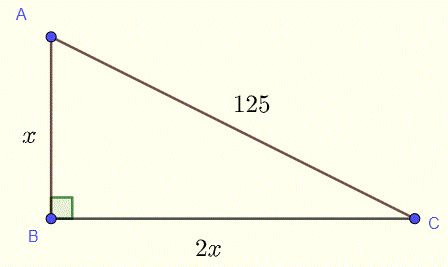
- \( 5 \)
- \( 15\)
- \( 10 \)
- \( 25\sqrt{5} \)
In the figure below AB is parallel to CD, and AD and CB intersect at the point O. Find \( x \) and \( y \).
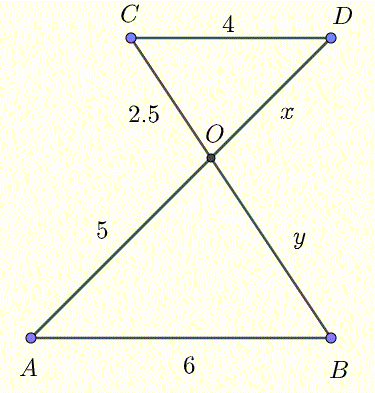
- \( x = 5 \; , \; y = 2.5\)
- \( x = 10/3 \; , \; y = 15/4\)
- \( x = 10/3 \; , \; y = 5/3\)
- \( x = 15/2 \; , \; y = 15/4\)
In the figure below, a square in inscribed in a circle. The shaded (light blue) region has an area of 10 unit2. Find the radius of the circle and round your answer to the nearest tenth.

- \( 2.5 \) units
- \( 3.0 \) units
- \( 3.5 \) units
- \( 4.0 \) units
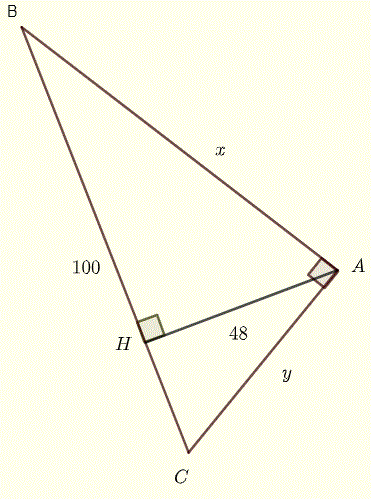
In the figure below, \( \overline{BC} = 100 \) and \( \overline{AH} = 48 \). Find \( x \) and \( y \), such that \( x \gt y \).
Find all internal angles of the parallelogram below whose area is 300 units2.

- \( \angle A = \angle C = 150^{\circ} \; , \; \angle B = \angle D = 30^{\circ} \)
- \( \angle A = \angle C = 150^{\circ} \; , \; \angle B = \angle D = 60^{\circ} \)
- \( \angle A = \angle C = 120^{\circ} \; , \; \angle B = \angle D = 60^{\circ} \)
- \( \angle A = \angle C = 140^{\circ} \; , \; \angle B = \angle D = 40^{\circ} \)
Find \( x \) so that the volume of the U-shaped rectangular structure is equal to \( 165 \) cm 3.

- \( 3 \)
- \( 4 \)
- \( 5 \)
- \( 6 \)
Statistics and Probabilities Questions to Practice for the EmSAT
The probability that Saef will watch the match on TV is 0.7 and the probability that his team wins is 0.5. What is the probability that Saef will not watch the match and his team wins the match?
- \( 0.35 \)
- \( 0.2 \)
- \( 0.1 \)
- \( 0.15 \)
A number is selected at random from the set: \( \{ -4,-1,0,2,5,6,7,10\} \). What is the probability that the number is either negative or greater than 6?
- \( 1/4 \)
- \( 1/3 \)
- \( 1/2 \)
- \( 1/8 \)
The probability that Sultan travels to Spain is 0.5. The probability that he will travel to Spain and then England is 0.3. If Sultan travels to Spain, what is the probability that he will travel to England as well?
- \( 0.6 \)
- \( 0.15 \)
- \( 0.2 \)
- \( 0.1 \)
Two brothers and 4 sisters in the same family study in high school. The average score of the 2 brother, at the end of the term, was 89 and the average of their 4 sisters was 92. What was the average of all the 6 brothers and sisters?
- \( 89 \)
- \( 91 \)
- \( 90 \)
- \( 92 \)
The scores of a test are normally distributed with a mean of 500 and a standard deviation of 100. What is the percentage of students who scored below 590 at this test? Round your answer to the nearest one percent.
- \( 75 \)
- \( 60 \)
- \( 82 \)
- \( 78 \)
Majed can either win or loose when playing a game. The probability that Majed wins a game against anyone of his friends is \( \dfrac{3}{4} \). What is the probability that Majed wins exactly 2 out of the next three games?
- \( \dfrac{1}{64} \)
- \( \dfrac{3}{64} \)
- \( \dfrac{9}{64} \)
- \( \dfrac{27}{64} \)
Calculus Questions to Practice for the EmSAT
Find the first derivative of the function \( f(x) = - 4x^3 + 3x^2 - 2x - 2 \).
Find the first derivative of the function \( f(x) = (x^3 - 2x^2 + x)(2x - 7) \).
Find the first derivative of the function \( f(x) = \sqrt{-3x+3} \).
Find the second derivative of the function \( f(x) = (x^2+1)^5 \).
Find the first derivative of the function \( f(x) = \dfrac{1}{x-1} \).
Find \( f'(2) \) if \( f(x) = \dfrac{x-1}{x+3} \).
- \( 1 \)
- \( 4 / 25 \)
- \( 1 / 5\)
- \( 4/5 \)
Find \( f'(x) \) if \( f(x) = \cos(2x - 2) \).
- \( - \sin(2x - 2) \)
- \( - 2x \sin(2x - 2) \)
- \( 2\sin \left(2x-2\right) \)
- \( -2\sin \left(2x-2\right) \)
Find the value of the constant \( k \) if \( f'(1) = 0 \) and \( f(x) = k x^2 + 2x -1 \).
- \( -1 \)
- \( -2 \)
- \( 0 \)
- \( 1 \)
Find all values of \( x \) that make the first derivative of the function \( f(x) = \dfrac{2x^2 + x}{x^2-1} \) equal to zero.
- \( -1/2 \; , \; 0 \)
- \( x=2-\sqrt{3} \; , \; x=2+\sqrt{3} \)
- \( x=-2-\sqrt{3} \; , \; x=-2+\sqrt{3} \)
- \( -1 \; , \; 1 \)
Find the limit \( \lim_{x\to\infty} \dfrac{x^3-2x+4}{-2x^3+x^2-1} \).
- \( + \infty \)
- \( -1/2 \)
- \( 0 \)
- \( -4 \)
Find the limit \( \lim_{x\to + 4} \dfrac{\sqrt{x} - 2}{x - 4} \).
- \( 0 \)
- \( 2 \)
- \( 4 \)
- \( 1/4 \)
Find the limit \( \lim_{x\to - 3} \dfrac{x^2 + 4x + 3}{x^2 - 9} \).
- \( 0 \)
- \( -1 \)
- \( 1/3 \)
- \( \infty \)