Free Compass Math Test Practice Questions
Solutions with Explanations - Sample 1
Solutions with explanations to compass math test practice questions in sample 1.

    A - Numerical Skills/Pre-Algebra


  1. compass problem 1

    Solution

    Use order of operation to evaluate multiplication and division first from left to right 9 ÷ 3 · 2 = 6
    Insert the result in the whole expression 72 - 6 + 2
    Evaluate addition and subtraction from left to right to obtain final value of expression 72 - 6 + 2 = 68

  2. In scientific notation, 3.0 x 10-5 + 0.0000022 =

    Solution

    We first rewrite 0.0000022 using 10-5 as follows  0.0000022 = 0.22 ×10-5
    We now add 3.0 x 10-5 and  0.22 ×10-5   as follows 3.0 x 10-5 +  0.22 ×10-5

    = 10-5 (3.0 + 0.22)

    = 3.22 x 10-5



  3. If

    compass problem 3.


    is calculated and the fraction obtained reduced to simplest form, then what is its numerator?

    Solution

    Reduce all fractions to the least common denominator 12, add, subtract and reduce the final result. 2 / 3 + (1 / 2 - 1 / 6) + (1 / 3 - 3 / 4)

    = 8 / 12 + (6 / 12 - 2 / 12) + (4 / 12 - 9 / 12)

    = (8 + 6 - 2 + 4 - 9) / 12

    = 7 / 12
    The numerator after reduction is

    7


  4. compass problem 4.



    Solution

    Evaluate expressions inside brackets 4 / 3 × 3 / 5 = 4 / 5

    1 / 4  ÷ 4 / 5 = 1 / 4 × 5 / 4 = 5 / 16
    Substitute expressions inside brackets by their values found above

    1 / 4 + (4 / 3 × 3 / 5) - (1 / 4 ÷ 4 / 5)

    =  1 / 4 + 4 / 5 - 5 / 16
    Reduce to the least common  denominator 80 and evaluate from left to right to obtain the final answer.

    = 20 / 80 + 64 / 80 - 25 / 80

    =  59 / 80


  5. A shop owner increased the selling price of a shirt from $20 to $26. By what percentage was the price increased?

    Solution

    Original price 20
    Selling price 26
    Difference / change 26 - 20 = 6
    Relative change change / original price = 6 / 20
    Change fraction into percent 6 / 20 = 30 / 100 = 30 %



  6. 3/4+0.85+20% =


    Solution

    Given expression 3 / 4 + 0.85 + 20 %
    Change fraction into decimal number (divide) 3 / 4 = 0.75
    Change 20% to decimal 20% = 20 / 100 = 0.2
    Evaluate the given express using decimal forms 3 / 4 + 0.85 + 20 %

    = 0.75 + 0.85 + 0.2

    = 1.8

  7. Tom worked for 6 hours and was paid $5.50 per hour. He then went shopping and bought two magazines at $9.50 each and a pen at $8.25. How much money does Tom have left?

    Solution

    Tom worked 6 hours at $5.50 per hour; he earned 6 × $5.50 = $33
    Shopping 2 magazines at $9.50 each 2 × $9.50 = $19
    Shopping a pen at $8.25 $8.25
    Total Shopping (he spent) $19 + $8.25 = $27.25
    Tom has left = what he earned - what he spent  $33 -  $27.25 = $5.75

  8. Bill bought 1(3/4) pounds of Cheddar cheese, 3.75 pounds of blue cheese and 4(1/2) pounds of goat cheese. How many pounds of cheese did Bill buy?

    Solution

    Change the mixed number 1 (3/4) into decimal number 1 (3/4) = 1.75
    Change the mixed number 4 (1/2) into decimal number 4 (1/2) = 4.5
    Total amount of cheese bought 1 (3/4) + 3.75 + 4 (1/2)

    = 1.75 + 3.75 + 4.5

    = 10 pounds

  9. In a certain school, 40% of all students are 8 years old or younger. The number of the remaining students is 120. How many students are 8 years old or younger?

    Solution

    Let x be the total number of students x
    Number of students that are 8 years old or younger is given by 40% x
    Remaining students 120 students

    or 100% - 40% = 60%  of total

    or 60% x
    Hence 60% x = 120 or x = 120 / 60%
    Number of students that are 8 years old or younger is given by 40% x = 40% (120 / 60%) = 80

  10. 1/5 of students in a school have no brothers or sisters. Of the remaining students, 40% have 1 brother or sister. What percent of all students have more than 1 brother or sister?

    Solution

    Let x be the total number of students x
    Number of students with no brothers or sisters 1/5 of x = x(1/5)
    Number of students with brothers or sisters (1 - 1/5) = (4/5) x
    40% of those with brothers or sisters have only one brother or sister 40% of (4 / 5) x = 40% (4/5) x
    Students with more than one brother or sister (100% - 40%) of (4 / 5) x = 60% (4 / 5) x = 48 % x
    Percent of all students with more than one brother or sister is 48 %

  11. A car hire company offers two plans A and B. In plan A, a customer pays a flat fee of $20 for the day plus 5 cents for each kilometer. In plan B, a customer pays a flat fee of $15 for the day plus 7 cents for each kilometer. For how many kilometers would a customer pay the same amount for the two plans?

    Solution

    Let x be the number of km x
    The cost CA for plan A is given by CA = 20 + 0.05 x
    The cost CB for plan B is given by CB = 15 + 0.07 x
    Same amount paid CA = CB

    20 + 0.05 x = 15 + 0.07 x
     Solve the above equation to find x which is the number of km so that a customer would pay the same amount. 20 - 15 = 0.07 x - 0.05 x

    x = 250

  12. Joe worked part time for x hours and earned y dollars. How much does he earn if he works z hours?

    Solution

    Earn y dollars in x hours, earn per hour y / x
    Earn in z hours z (y / x) = z y / x

  13. In a science test, a class of 30 students had an average of 80. The 20 girls in the class had an average of 85. What is the average of the 10 boys in the class?

    Solution

    Let T be the total of marks for the 30 students. If average is 80, then T / 30 = 80

    T = 30 * 80 = 2400
    Let TG be the total marks for the 20 girls. If average is 85, then TG / 20 = 85

    TG = 20 * 85 = 1700
    Let TB be the total marks for the 10 boys, then TB = 2400 - 1700 = 700
    Average for boys is given by 700 / 10 = 70

  14. Find y if y / 5 = 10 / 25.

    Solution

    Given equation y / 5 = 10 / 25
    Cross product gives 25 y = 5 * 10
    Solve for y y = 2

  15. √(32 + 42) =

    Solution

    Given expression √(32 + 42)
    Simplify expression inside radical 32 +  42 = 9 + 16 = 25
    Simplify given expression by taking square root √(32 + 42) = √25 = 5

    B - Algebra

  16. If a = -2 and b = -2, what is the value of (a3 - 1) / (b - 1)

    Solution

    Given expression (a3 - 1) / (b - 1)
    Substitute a by -2 and b by -2 in given expression ((-2)3 - 1) / ((-2) - 1)
    Simplify expression above (-8 - 1) / (-2 - 1) = 3

  17. If -2(x + 9) = 20, then - 4x =

    Solution

    Given equation -2(x + 9) = 20
    Solve for x -2x - 18 = 20

    -2x = 38

    x = -19
    Substitute x in - 4x by  - 19 - 4 x = - 4 (-19) = 76

  18. x is a variable such that if 20% of it is added to its fifth the result is equal to 12 subtracted from seven tenths of x. Find x.

    Solution

    x is a variable x
    20% of it 20% x
    its fifth (1 / 5) x
    x is a variable such that if 20% of it is added to its fifth 20% x + (1 / 5) x
    seven tenths of x (7 / 10) x = 0.7 x
    the result is equal to 12 subtracted from seven tenths of x 20% x + (1 / 5) x = 0.7x - 12
    Change % and fractions to decimal numbers 0.2 x + 0.2 x = 0.7x - 12
    Solve for x 12 = 0.3 x

    x = 40

  19. The area A of a trapezoid is given by the formula A = 0.5 (b + B) h, where b and B are the sizes of the bases and h the size of the height of the trapezoid. Express B in terms of A, b and h.

    Solution

    Given formula A = 0.5 (b + B) h
    Divide both sides of the formula by 0.5 h and simplify (A / 0.5 h) = b + B
    Solve for B B = (A / 0.5 h) - b
    Note that 1 / 0.5 = 2, hence B = 2 A / h - b

  20. Tom, Linda and Alex have $120 dollars. Alex has the third of what Tom has and Linda has twice as much as Alex. How much money, in dollars, does Linda have?

    Solution

    Let x be the amount of money in dollars that Tom has x
    Alex has the third of Tom (1 / 3) x
    Linda has twice as much as Alex 2 (1 / 3) x
    All together they have 120 dollars, hence x + x / 3 + 2 x / 3 = 120
    Multiply all terms of the above equation, simplify and solve for x 3 x + x + 2 x  = 360

    x = 60
    Linda has 2 (1 / 3) x = (2 / 3) 60 = $40

  21. Which of the following is equivalent to 6x2 - 11x - 2?

    Solution

    Given 6x2 - 11x - 2
    The linear terms that will make the factors has coefficients 6 and 1 (since 6*1 = 6) or 2 and 3 (since 2*3=6) (6x     )(x       )

    (2x      )(3x     )
    The constant terms should -1 and 2 or 1 and -2 (6x - 1)(x + 2) 
    If (6x - 1)(x + 2) is expanded, it does not give 6x2 - 11x - 2. (6x - 1)(x + 2) = 6x2 + 11x - 2
    We now try (6x + 1)(x - 2) which when expanded gives 6x2 - 11x - 2 (6x + 1)(x - 2) = 6x2 - 11x - 2

  22. Which of the following is a factor of x2 - 7x - 8?

    Solution

    Given x2 - 7x - 8
    Factor (x + 1)(x - 8)
    One of the factors is x + 1

  23. (2xy2 - 3x2y) - (2x2y2 - 4x2y) =

    Solution

    Given (2xy2 - 3x2y) - (2x2y2 - 4x2y)
    Eliminate brackets taking signs into consideration = 2xy2 - 3x2y - 2x2y2 + 4x2y
    Group like terms - 3x2y and 4x2y = 2xy2  - 2x2y2 + x2y

  24. During the same journey, Stuart drove x miles for 2 hours, and 200 miles for 3 hours. Find x if the average speed for the entire journey is 70 miles per hour.

    Solution

    Average speed  = Total distance / total time = 70 miles/hour
    Total distance = x + 200   miles
    Total time = 2 + 3 = 5 hours
    Substitute in formula above (x + 200) / 5 = 70
    Solve above equation for x x + 200 = 350

    x = 150 miles

  25. Given the equations of the lines
    (I) 2y + 3x = 3
    (II) -3y - 2x = 5
    (III) -6y + 4x = 9,
    (IV) 2y + 6x = 9
    which two lines are perpendicular?

    Solution

    Rewrite all 4 equations in slope intercept form (I) y = (- 3 / 2) x + 3 / 2

    (II) y = (-2 / 3) x - 5 / 3

    (III) y = (2 / 3) x - 3 / 2

    (IV) y = - 3x + 9 / 2
    The slopes of all 4 lines are (I) -3/2

    (II) -2/3

    (III) 2/3

    (IV) -3
    For two lines with slopes m and n to be perpendicular, the product of their slopes must equal -1 or m*n = -1. The product of the slopes of (I) and (III) gives -1; and hence (I) and (III) are perpendicular. (-3 / 2)*(2 / 3) = -1

  26. If f(x) = (x + 1)2, then f(t + 2) =

    Solution

    Given f (x) = (x + 1)2
    To find f (t + 2), we substitute x by t + 2 in f (x); hence f (t + 2) = ((t + 2)+ 1)2

    = (t + 3)2

    = t 2 + 6t + 9

  27. For x > 0 and y > 0,
    (√x + √y) (√x - √y) - (√x - √y)2 =


    Solution

    Given (√x + √y) (√x - √y) - (√x - √y)2
    Expand (√x + √y) (√x - √y) (√x + √y) (√x - √y) = x - y
    Expand (√x - √y)2 (√x - √y)2 = x + y - 2√x √y
    Hence (√x + √y) (√x - √y) - (√x - √y)2

    = (x - y) - (x + y - 2√x √y)

    = - 2 y + 2√x √y

  28. What is the slope of the line whose equation is given by
    x / 2 - y / 4 = 7


    Solution

    Equation of line given in standard form x / 2 - y / 4 = 7

    To determine the slope, we need to write in slope intercept form. Multiply all terms by 4 and simplify and solve for y.

    		 2 x - y = 38

    y = 2x - 38
    Slope is the coefficient of x 2

  29. For x > 3,
    (x / (x - 3) + 1 / 2)(2/(x - 1)) =


    Solution

    Given (x / (x - 3) + 1 / 2) (2 / (x - 1))

    We first simplify, if possible, the expression on the left side. Reduce to the lowest common denominator.

    ( x / (x - 3) + 1 / 2)

    =  2x / ( 2 (x - 3) ) + ( x- 3)  / (2 (x - 3))

    = (3x - 3) / (2(x - 3))

    Hence x / (x - 3) + 1 / 2) (2 / (x - 1))

    = (3x - 3) (2/(x - 1))) / (2(x - 3))

    = 3(x - 1)(2 / (x - 1)) / (2(x- 3))
    Simplify

    = 3 / (x - 3)

  30. In a standard rectangular system of axes, point A has the coordinates (2 , 1). What must be the coordinates of point B if M(3 , 2) is the midpoint of the segment AB?

    Solution

    Let a and b be the x and y coordinates of point B, hence M is the midpoint of A and B
    Since the midpoint M(3,2) is known and point A(2,1) is also known, we can write (3,2) = ( (2 + a)/2 , (1 + b)/2 )
    Two equations may be written as follows 3 = (2 + a) / 2 and 2 = (1 + b) / 2
    Solve for a and b a = 4 and b = 3

    C - College Algebra

  31. What is the value of X in the following geometric sequence
    X , 64 , ___ , ___ , 8


    Solution

    Let r be the common ratio of the geometric sequence. Hence the terms of the sequence may be written as X , 64 , __ , ___ , 8

    or

    X , r X , r 2 X , r 3 X , r 4 X
    Two terms are known, the second and the last. Hence r X = 64 and  r 4 X = 8
    Divide the left hand side and the right hand side of the two equations in order to eliminate X, simplify and solve for r. r 4 X / r X = 8 / 64

    r 3 = 1 / 8

    r = 1 / 2
    The second term is equal to 64 and also given by r X; write the equation and solve for X. (1/2) X = 64

    X = 128

  32. For what value of K will the system of equations given below have no solution?

    2x + 5y = 9
    -3x - K y = 4


    The given system of equations will not have solutions if its determinant is equal to 0. Hence 2(-K) - 5 (-3) = 0
    Solve the above for K K = 15 / 2

  33. If f(x) and g(x) are two functions defined by

    f(x) = √(x + 1)
    g(x) = | x - 1 |,

    then what is the value of f(g(9))?

    Solution

    f and g given f (x) = √(x + 1) and g (x) = | x - 1 |
    Hence f (g(9)) = f(|9 - 1|)

    = f(|8|)

    = f(8)

    = √(8 + 1) = 3

  34. The range of

    f(x) = x2 -2x + 1
    is given by the interval

    Solution

    Given f (x) = x2 -2x + 1

    f is a quadratic function and its graph is a parabola that opens up since its leading coefficient is positive and therefore has a minimum point which is also the vertex. The coordinates of the vertex V of the graph of is given by

    		V (h , k) = (-b/2a , f(-b/2a))

    = (1 , 0)
    Since (1 , 0) is a minimum point, the range of values of f(x) is given by the interval [ 0 , + infinity)

  35. If f(x) is a linear function such that f(-1) = 11 and f(2) = 5,
    then f(0) =

    Solution

    f(x) is a linear function which may be written as f (x) = m x + b , where m and b are real numbers

    f(-1) = 11 and f(2) = 5 give the following equations

    		 - m + b = 11

    2m + b = 5
    We need to find f(0) = b. Hence solve the above system of equations for b. Multiply all terms in the equation - m + b = 11 by 2 and rewrite the system as follows -2m + 2 b = 22

    2m + b = 5
    Add the sides of the two equations, solve and evaluate f(0). 3 b = 27

    b = 9

    f(0) = 9

  36. Which of these functions is(are) always increasing?
    (I) f(x) = -x2 + 2x + 1
    (II) f(x) = 2x - 1000
    (III) f(x) = |x - 4| + 255
    (IV) f(x) = -e-x,

    Solution

    Given
    (I) f(x) = -x2 + 2x + 1
    (II) f(x) = 2x - 1000
    (III) f(x) = |x - 4| + 255
    (IV) f(x) = - e -x,

    Function (I) is a quadratic one and therefore is not always increasing.
    Function (II) is a linear function with positive slope and therefore always increasing.
    Function (III) contains an absolute value and its graph is V shaped and therefore is not always increasing.
    Function (IV): e -x is an exponential function with base equal to 1/e and therefore less than 1 and hence always decreasing but when multiplied by -1 it becomes always increasing. Hence f(x) = - e -x is always increasing.

    		Of all the functions given the ones in (II) and (IV) are always increasing.

  37. i is the imaginary unit such that i = √-1. What is the value if i99?

    Solution

    Note that
    i 4 = 1 , where i is the imaginary unit

    We need to evaluate i 99. Divide 99 by 4 and write 99 as follows

    		 99 = 4 * 24 + 3

    Hence

    		 i 99 = i (4*24 + 3)

    = (i 4) 24  i3

    = 1 * i3 = - i



  38. If

    compass test problem 38.

    Find a, b and c.

    Solution

    Multiply row [3 , 2] in the first matrix by column [0 , b] in the second matrix and equate it to the corresponding term in the third matrix.
    3*0 + 2*b = - 4

    Multiply row [3 , 2] in the first matrix by column [a , c] in the second matrix and equate it to the corresponding term in the third matrix.

    		 3*a + 2*c = 9
    Multiply row [-1 , - 2] in the first matrix by column [a , c] in the second matrix and equate it to the corresponding term in the third matrix. - a - 2 c = - 7
    Solve the first equation to find b and solve simultaneously the second and third equations to find a and c. Hence a = 1, b = -2 and c = 3


  39. In an arithmetic series, the 3rd term is equal to 114 and the last term is equal to -27. The sum of all terms in the series is equal to 2325. What are the last three terms in the series?

    Solution

    Let a be the first term of the series, d be the common difference. The third term given by a + 2d is equal to 114. Hence
    (I)  a + 2 d = 114

    Let n be the number of terms in the series. The last term is given by a + (n - 1)d and is equal to - 27. Hence

    		(II)  a + (n - 1) d = -27
    The sum of the n terms is given by (n / 2)(a - 27) and is equal to 2325. Hence (III)  (n / 2)(a - 27) = 2325
    Equation (I) gives a = 114 - 2d
    Substitute a by 114 - 2d in equations II and III (II)  114 - 2d + (n - 1)d = -27

    (III)  (n / 2)(114 - 2d - 27) = 2325
    Group multiply all terms of equation (III) group like terms and simplify to obtain (II) n d - 3d = -141

    (III) 87n - 2 n d = 4650
    Solve equation (II) for d d = -141 / (n - 3)
    Substitute d by -141 / (n - 3) in equation (III) 87n - 2n (-141 / (n - 3)) = 4650
    Expand and simplify and set the numerator equal to zero to obtain the quadratic equation. 87n2 - 4629 n + 13950 = 0
    Solve the above equation for integer n to find n = 50 and n = 93 / 29
    Only n = 50 is a solution since it is an integer. Find d using the above equation d = -141 / (n - 3) = -141 / (50 - 3) = - 3
    Last term is equal to -27 and hence the last three terms are equal to -27

    -27 - d = -24

    -24 - d = -21

    D - Geometry


  40. In the figure below, line T1 is parallel to line T2 and line L1 is parallel to line L2. The pair of lines T1 , T2 are not perpendicular to L1,L2. Which of the set of angles below has all 4 angles equal in measurement?

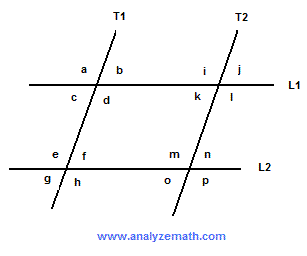    compass test problem 40.


    A) {a,b,c,d}
    B) {e,f,g,h}
    C) {e,f,m,h}
    D) {j,k,f,g}
    E) {a,b,f,g}

    Solution

    Angles j and k are verticcal angles and therefore are equal in size. Angles f and g are also vertical angles and equal in size. Angles j and f are corresponding angles to the same angle n and are therofore equal in size. Hence all angles in the set {j,k,f,g} in D) are equal in size.


  41. A cube with edge length x and a right cylinder with circular base have the same volume. Find x ,in cm, if the radius of the cylinder is 5 cm and its height is 5 cm.

    Solution

    Volume V of cylinder is given by

    V = height*area of base = 5 * (pi*52) = 125 pi

    Volume W of cube with edge x is given by

    W = x3

    The two volumes are equal

    x3 = 125 Pi

    Solve above for x

    x = 5 (Pi)1/3


  42. Find, in square cm, the area of an equilateral triangle of side 20 cm.

    Solution

    Draw the altitude from one vertex and make a right triangle of legs h and x/2 and hypotenuse x. The altitude h of the triangle

    h = √ (x2 - (x/2)2) = (x/2) √3

    The area A of the triangle is given by

    A = (1/2) x (x/2) √3 = 100 √3


  43. The two circles shown below have diameters AB and BD and are tangent at B. ABC and BDE are isosceles triangles inscribed inside the circles. What is the measurement, in degrees, of angle CBE?

    compass test problem 43.

    Solution

    Since AB is the diameter of the circle, then ABC is a right triangle. Since it is isosceles the size of angle CBA is 45 degrees. Since BD is the diameter of the circle, then BDE is a right triangle. Since it is isosceles, the size of angle EBD is 45 degrees.

    Since the circles are tangent at B, the points A, B and D are collinear and therefore the sum of the sizes of angles CBA, CBE and EBD is equal to 180 degrees which gives the size of angle CBE of 90 degrees.


  44. In the figure below, EB and FC are both perpendicular to AC and x is the length of AB. If the length of AC is 11, what is x?

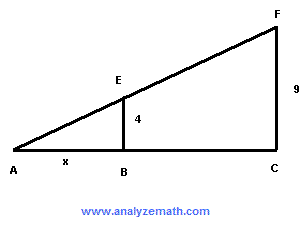    compass test problem 44.


    Solution

    Since EB and FC are perpendicular to the same line, they are parallel and therefore triangles ABE and ACF are similar and the proportionality of the corresponding sides gives

    x / 11 = 4 / 9

    solve for x: x = 44 / 9


  45. ABC is a right triangle such that the length of BC is 5 units. The legs have length x and 2x. Find x.

    compass test problem 45.

    Solution

    Since the triangle is right we use Pythagora's theorem

    x2 + (2x)2 = 52

    5 x2 = 52

    solve for x: x = √5


  46. AB is tangent to the circle with center O and radius 10 cm. The length of OA is 15 cm and the length of OB is 20 cm. Find the area, in square cm, of triangle ABO.

    compass test problem 46.


    Solution

    If the altitude from vertex o to the base AB is drawn, we end up with two right triangles of hypotenuses 15 and 20 cm. Let T being the point of tangency of AB and the circle. The remaining legs of the two triangles may be found using Pythagora's theorem.

    AT2 = 152 - 102 = 125

    BT2 = 202 - 102 = 300

    AT = 5 √ 5

    BT = 10 √ 3

    The area of triangle ABO is given by

    (1/2)*OT*(AT + BT) = (1/2)*10*(5 √ 5 + 10 √ 3)

    = 25 √ 5 + 50 √ 3


  47. The area of the trapezoid shown below is 128 square cm. Find x in cm.

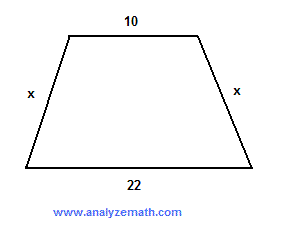    compass test problem 47.

    Solution

    If h is the altitude of the trapezoid, then the area is given by

    (1/2)*h*(10 + 22) = 128

    solve for h: h = 8

    If we draw an altitude so that side x, the altitude and part of the lower base form a right triangle, then the length of that part of the lower base is equal to

    (22 - 10) / 2 = 6

    We now use Pythagora's theorem to find x

    x2 = 82 + 62

    solve for x: x = 10


  48. C1, C2 and C3 are three tangent circles with their centers on the same line. If R is the radius of the large circle and the diameter of circle C1 is twice the diameter of circle C3, then what is the area of the shaded region?

    compass test problem 48.

    Solution

    The area of the largest circle is given by.

    Pi R2

    The sum of the diameters of C1 and C3 is equal to the diameter of the largest circle which is 2R. The diameter of C1 is twice that of C3. Hence the diameter of C3 is given by

    2 R / 3 and its radius is 2 R / 6

    and the diameter of C1 is given by

    4 R / 3 and its radius is 4 R / 6

    Area of C1 is given by

    Pi (4 R / 6)2

    Area of C3 is given by

    Pi (2 R / 6)2

    Area of shaded region is given by area of largest circle minus area of C1 and area of C3

    Pi R2 - Pi (4 R / 6)2 - Pi (2 R / 6)2

    = (4 / 9)R2Pi

    E - Trigonometry


  49. If x is a positive angle smaller than 90° and cos(x) = 1/3, then sin(x) =

    Solution

    Use the identity sin2x + cos2x = 1 to find sin x as follows

    sin2x = 1 - cos2x

    Solve for sin x

    sin x = + or - √(1 - cos2x)

    Since x is positive and less than 90 degrees, sin x is positive and hence

    sin x = + √(1 - cos2x)

    = √( 1 - (1/3)2 ) = 2 √2 / 3


  50. Convert 135° into radians.
    Solution

    135° = (135° * Pi) / 180° = 3 Pi / 4

  51. The measurement of an angle of a right triangle is 40° and the leg opposite to this angle is 5 cm long. What is the length, in cm, of the other leg?

    Solution

    Let us use the definition of the tangent

    tan(40°) = opposite side / adjacent side = 5 / adjacent side

    solve to find adjacent side

    adjacent side (second leg) = 5 / tan(40°)


  52. Which of these graphs is the graph of y = cos(2x)?

    compass test problem 52.

    Solution

    Graphs C and E do not satisfy the fact that y = 1 at x = 0. The period of y = cos(2x) is given by

    2 Pi / 2 = Pi

    Graphs B has a period equal to Pi and is the graph of y = cos(2x).

  53. What is the smallest positive value of x for which y = cos(3x) has a minimum value?

    Solution

    The smallest positive value of A that makes cos(A) minimum is Pi. If instead of cos(A) we have cos(3x), then the smallest value of 3x that makes cos(3x) minimum is also Pi. Hence

    3x = Pi

    x = Pi / 3 is the smallest positive value of x that makes cos(3x) minimum.


  54. If you put 6 equilateral triangles together as shown below, you can make a regular hexagon. What is the area, in square units, of a regular hexagon of side lenght 6 units?

    compass test problem 54.


    Solution

    The altitude h of an equilateral triangle of side 6 is given by

    h = √(62 - 32) = 3 √ 3

    The area of an equilateral triangle of side 6 is given by

    (12)*6*3 √ 3 = 9 √ 3

    The area of the hexagon is given by

    6*9 √ 3 = 54 √ 3

More ACT, SAT and Compass practice