Definición y ecuación de una hipérbola con eje transversal horizontal
Una yperbola es el conjunto de todos los puntos \( M(x,y)\) en un plano tal que la diferencia de las distancias de \( M \) a los puntos fijos \( F_1 \) y \( F_2 \) llamados focos (plural de foco) es igual a una constante.
\( \overline{MF_2} - \overline{MF_1} = \sqrt{(x+c)^2+y^2} - \sqrt{(x-c)^2+y^2} = \pm 2 a \)
Eliminando las raíces cuadradas elevando al cuadrado y simplificando usando la relación \( c^2 = a^2 + b^2\), la ecuación estándar de una hipérbola se puede escribir como:
\( \dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1 \)
donde \( a \gt 0\), \( b \gt 0\) y \( c \gt 0\).
El punto \(O(0,0)\) es el centro de la hipérbola.
Los puntos \( V_1(a,0) \) y \( V_2(-a,0) \) se llaman vértices de la elipse.
Los focos están en \( F_1(c,0) \) y \( F_2(-c,0) \)
Asíntotas de la hipérbola
Si resolvemos la ecuación de la hipérbola para \( y \), obtenemos
\( y = \pm \dfrac{b}{a} \sqrt{x^2 - a^2} \)
A medida que \( |x| \) aumenta indefinidamente, \( y \) se aproxima a \(\pm \dfrac{b}{a} x \). Por lo tanto, las rectas con ecuaciones \( y = \pm \dfrac{b}{a} x \) se llaman asíntotas de la hipérbola.
A continuación se muestra la gráfica de una hipérbola y sus asíntotas (líneas discontinuas).
Ejemplo 1
Una hipérbola, con eje transversal horizontal, centrada en \( (0,0) \) tiene x intercepta en \( (3,0) \) y \( ( -3 ,0) \) y focos en \( (5 ,0) \) y \( (-5,0) \). Encuentra la ecuación de la hipérbola y sus asíntotas.
Solución al ejemplo 1
Las intersecciones x de una hipérbola con eje transversal horizontal son los vértices dados por \( (a , 0) \) y \( (-a , 0) \) . Por lo tanto \( a = 3 \)
Los focos están dados por \( F_1(c,0) = F_1(5,0)\) y \( F_2(-c,0) = F_2(-5,0)\). Por lo tanto \( c = 5 \)
\(a \), \(b \) y \(c \) están relacionados por \( c^2 = a^2 + b^2\) lo que da la ecuación
\( 5^2 = 3^2 + b^2\)
resolver para obtener
\( segundo = 4 \)
La ecuación de la hipérbola viene dada por
\( \dfrac{x^2}{3^2} - \dfrac{y^2}{4^4} = 1 \)
Ecuación general
Podemos generalizar y escribir la ecuación de una hipérbola cuyo centro está en \( O(h,k) \) de la siguiente manera
con focos en \( F_1(c+h,k) \) y \( F_2(-c+h,k) \) y vértices en \( V_1(a+h,k) \) y \( V_2(- a+h,k) \), y la relación \( c^2 = a^2 + b^2\).
Las asíntotas están dadas por \( y = \pm \dfrac{b}{a} (x - h) + k\)
Ejemplo 2
Encuentra la ecuación de la hipérbola con vértices en \( V_1(2,2) \) y \( V_2(-4,2) \) y cuyas asíntotas están dadas por las ecuaciones \( y = \pm \dfrac{2} {5} (x - h) + k_0 \) donde K_0 es una constante. Encuentra las ecuaciones de las asíntotas y traza la gráfica de la hipérbola dada y sus asíntotas.
Solución al ejemplo 2
Los vértices están dados por \( V_1(a+h,k) = V_1(2,2) \) y \( V_2(-a+h,k) = V_2(-4,2) \)
lo que da \( k = 2 \) y \( a+h = 2 \) y \( -a+h = - 4 \)
Resuelva las dos últimas ecuaciones en \( a \) y \( h \) para obtener
\(a = 3\) y \(h = -1 \)
Las asíntotas están dadas por \( y = = \pm \dfrac{2}{5} (x - h) + K_0 = \pm \dfrac{b}{a} (x - h) + k \)
Por lo tanto \( \dfrac{b}{a} = \dfrac{2}{5} \)
Sustituya \( a \) por \( 3 \) en la ecuación anterior y resuelva para \( b \) para obtener
\(b = \dfrac{6}{5}\)
\( K_0 = k = 2 \)
Las ecuaciones de las asíntotas están dadas por
\( y = = \pm \dfrac{2}{5} (x - h) + 2 \)
Ecuación de una hipérbola con eje transversal vertical
La ecuación de una hipérbola con eje transversal vertical cuyo centro está en \( O(h,k) \) está dada por
con focos en \( F_1(h,k+c) \) y \( F_2(h,k-c) \) y vértices en \( V_1(h,k+a) \) y \( V_2(h,k-a) \), y la relación \( c^2 = a^2 + b^2\).
Las asíntotas están dadas por \( y = \pm \dfrac{a}{b} (x - h) + k\)
Ejemplo 3
La ecuación de una hipérbola viene dada por \( \dfrac{(y-2)^2}{3^2} - \dfrac{(x+3)^2}{2^2} = 1 \). Encuentra su centro, focos, vértices y asíntotas y grafica.
Solución al ejemplo 3
La ecuación dada es la de una hipérbola con un eje transversal vertical. Compárelo con la ecuación general dada arriba, podemos escribir
\( h = -3, k = 2, a = 3\) y \( b = 2, c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 2^2} = \sqrt{13}\)
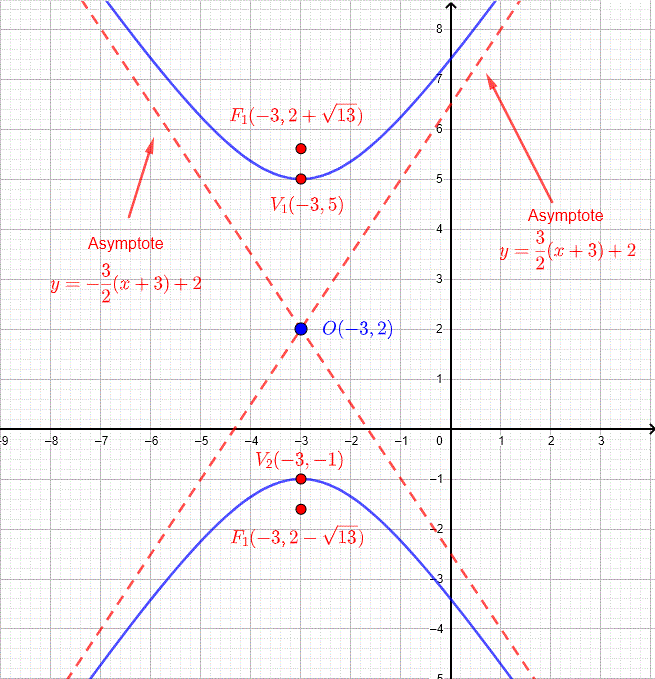
El centro está en \( O(h,k) = O(-3,2) \)
Los focos están en \( F_1(h,k+c) = F_1(-3,2+\sqrt{13})\) y \( F_2(-3,2-\sqrt{13}) \)
Los vértices están en \( V_1(h,k+a) = V_1(-3,5) \) y \( V_2(h,k-a) = V_2(-3,-1) \)
Las ecuaciones de las asíntotas están dadas por
\( y = \dfrac{3}{2}(x + 3) + 2 \) y \( y = - \dfrac{3}{2}(x + 3) + 2 \)
A continuación se muestra la gráfica de la ecuación dada de la hipérbola, su centro, focos, vértices y asíntotas.
Tutorial interactivo sobre la ecuación de una hipérbola con eje transversal horizontal
Ahora se presenta una aplicación para explorar la ecuación de una hipérbola y sus propiedades. La ecuación utilizada es la ecuación estándar que tiene la forma
La exploración se lleva a cabo cambiando los parámetros \( a, b, h \) y \( k \) incluidos en la ecuación anterior de la hipérbola. Los valores predeterminados, al abrir esta página, son: \( a = 2, b = 3, h = -1 \) y \( k = 2 \).
Algunas actividades se enumeran a continuación, pero se pueden generar muchas otras actividades.
Haga clic en el botón "Plot Equation" para comenzar.
Pase el cursor del mouse sobre el gráfico del punto trazado para leer las coordenadas.
Haga clic en el botón encima de "Plot Equation". Puede pasar el cursor sobre el gráfico para rastrear las coordenadas. También puede colocar el cursor mousse en la parte superior derecha del gráfico para tener la opción de descargar el gráfico como un archivo png.
1 - Selecciona un punto M en la gráfica de la hipérbola, pasa la mousse sobre él y lee las coordenadas. Lea las coordenadas de F1 y F2 (leyenda de la derecha) o coloque el mouse sobre la mousse y lea sus coordenadas y muestre que la diferencia de las distancias \( \overline{MF_1} - \overline{MF_2} \) está cerca de \( 2a\) si \( \overline{MF_1} \gt \overline{MF_2} \) o \( - 2a\) si \( \overline{MF_1} \lt \overline{MF_2} \).
Puedes realizar la actividad anterior para diferentes valores de \( a, b, h\) y \( k \) con tantos puntos como sean necesarios para comprender mejor la definición de hipérbola.
2 - Usa los valores de \( a \) y \( b \) para encontrar \( c \) usando la relación entre \( a, b\) y \( c \) dada por \( c^2 = a ^2 + b^2\).
Utilice los resultados anteriores para encontrar las coordenadas de \( F_1, F_2, V_1 \) y \( V_2 \) y verifique los resultados gráficamente.
3 - Establezca \( a, b, h\) y \( k \) en algunos valores. Encuentre las intersecciones xey y verifique sus resultados gráficamente.
4 - Ejercicio:
Demuestre mediante cálculos algebraicos que la siguiente ecuación \( \dfrac{(x + 2)^2}{5} - 5(y-3)^2 = 5 \) es la de una hipérbola y encuentre el centro, focos y vértices de la elipse dada por la ecuación, luego usa la aplicación para graficarla y verificar tus respuestas.
Más referencias y enlaces a temas relacionados con la ecuación de la hipérbola
