Cómo graficar y bosquejar funciones logarítmicas: un tutorial paso a paso. Se estudian en detalle propiedades como el dominio, el rango, las asíntotas verticales y los interceptos de las gráficas de estas funciones. También está disponible papel cuadriculado gratuito.
Comenzamos con las propiedades de la gráfica de la función logarítmica básica de base \( a \),
\[ f(x) = \log_a(x), \quad a > 0 \text{ y } a \neq 1 \]El dominio de la función \( f \) es el intervalo \( (0, +\infty) \). El rango de \( f \) es el intervalo \( (-\infty, +\infty) \).
La función \( f \) tiene una asíntota vertical dada por la recta \( x = 0 \). Esta función tiene un intercepto en \( x \) en el punto \( (1, 0) \), y \( f \) es creciente cuando \( x \) aumenta.
Puedes repasar todas estas propiedades de la función logarítmica de forma interactiva.
\( f \) es una función definida por
\[ f(x) = \log_2(x + 2) \]a – El dominio de \( f \) es el conjunto de todos los valores de \( x \) tales que
\[ x + 2 > 0 \]Al resolver la desigualdad se obtiene el dominio:
\[ x > -2 \]El rango de \( f \) es
\[ (-\infty, +\infty) \]b – La asíntota vertical se obtiene resolviendo la ecuación
\[ x + 2 = 0 \]lo que da
\[ x = -2 \]Cuando \( x \) se aproxima a \(-2\) por la derecha (\( x \to -2^+ \)), la función \( f(x) \) decrece sin límite.
c – Para encontrar el intercepto en \( x \), resolvemos \( f(x) = 0 \):
\[ \log_2(x + 2) = 0 \] \[ x + 2 = 2^0 \] \[ x = -1 \]El intercepto en \( x \) es \( (-1, 0) \).
El intercepto en \( y \) es \( (0, f(0)) \):
\[ f(0) = \log_2(2) = 1 \]Por lo tanto, el intercepto en \( y \) es \( (0, 1) \).
d – Con la información obtenida, se trazan más puntos y se dibuja la gráfica con una curva suave.
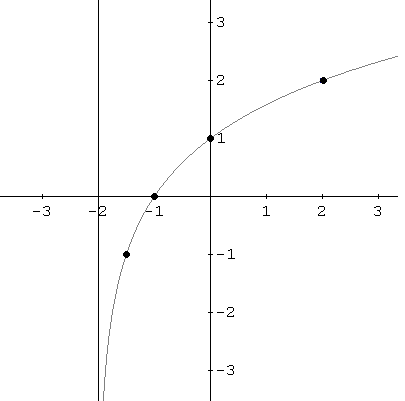
Sea \( f(x) = \log_2(x + 3) \).
Sea \( f \) una función definida por
\[ f(x) = -3 \ln(x - 4) \]a – El dominio de \( f \) es el conjunto de todos los valores de \( x \) tales que
\[ x - 4 > 0 \]Al resolver la desigualdad se obtiene el dominio:
\[ x > 4 \]El rango de \( f \) es el intervalo
\[ (-\infty, +\infty) \]b – La asíntota vertical se obtiene resolviendo la ecuación
\[ x - 4 = 0 \]lo que da
\[ x = 4 \]Cuando \( x \) se aproxima a 4 por la derecha (\( x > 4 \)), la función \( f(x) \) crece sin límite.
Algunos valores ilustrativos son:
\[ f(5) = -3 \ln(1) = 0 \] \[ f(4.001) = -3 \ln(0.001) \approx 20.72 \] \[ f(4.000001) = -3 \ln(0.000001) \approx 41.45 \]c – Para encontrar el intercepto en \( x \), resolvemos \( f(x) = 0 \):
\[ -3 \ln(x - 4) = 0 \] \[ \ln(x - 4) = 0 \] \[ x - 4 = e^0 \] \[ x = 5 \]El intercepto en \( x \) es \( (5, 0) \).
El intercepto en \( y \) no existe, ya que \( x = 0 \) no pertenece al dominio de \( f \).
d – Usamos puntos adicionales para trazar la gráfica:
\[ f(4.5) \approx 2.08,\quad f(8) \approx -4.16,\quad f(14) \approx -6.91 \]Se trazan los puntos, la asíntota vertical y se unen con una curva suave.

Sea \( f(x) = 2 \ln(x + 5) \).
Sea \( f \) una función definida por
\[ f(x) = 2 \ln(|x|) \]a – El dominio de \( f \) es el conjunto de todos los números reales tales que \( |x| > 0 \). Por lo tanto, el dominio es \( \mathbb{R} \setminus \{0\} \).
El rango de \( f \) es
\[ (-\infty, +\infty) \]b – La asíntota vertical se obtiene resolviendo
\[ |x| = 0 \]lo que da
\[ x = 0 \]Cuando \( x \to 0^+ \), \( f(x) \) decrece sin límite:
\[ f(1) = 0,\quad f(0.1) \approx -4.61,\quad f(0.0001) \approx -18.42 \]De manera similar, cuando \( x \to 0^- \), \( f(x) \) también decrece sin límite.
c – Para encontrar los interceptos en \( x \), resolvemos:
\[ 2 \ln(|x|) = 0 \] \[ |x| = 1 \]Las soluciones son \( x = -1 \) y \( x = 1 \). Por lo tanto, los interceptos en \( x \) son \( (-1,0) \) y \( (1,0) \).
No existe intercepto en \( y \) porque \( x = 0 \) no pertenece al dominio.
La función es par, ya que
\[ f(-x) = f(x) \]Su gráfica es simétrica respecto del eje \( y \).
Usamos puntos adicionales:
\[ f(4) \approx 2.77,\quad f(0.5) \approx -1.39 \]Se trazan los puntos, la asíntota vertical y se une con una curva suave.
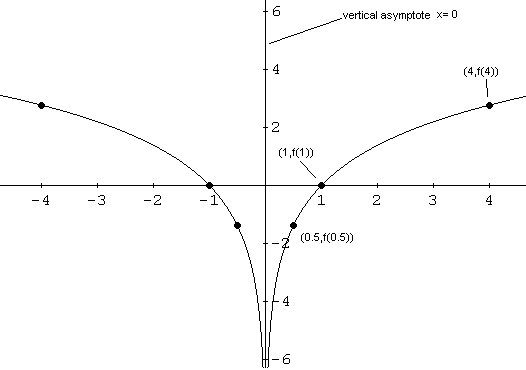
Sea \( f(x) = -2 \ln(x^2) \).