¿Cómo se grafica una función racional? Este tutorial paso a paso explica cómo hacerlo y analiza propiedades importantes como el dominio y las asíntotas verticales y horizontales. También está disponible papel milimetrado gratuito.
Una función racional \( f \) tiene la forma
\[ f(x) = \dfrac{g(x)}{h(x)} \]donde \( g(x) \) y \( h(x) \) son funciones polinómicas.
El dominio de \( f \) es el conjunto de todos los números reales excepto aquellos valores de \( x \) que hacen que el denominador \( h(x) \) sea igual a cero.
En lo que sigue, suponemos que \( g(x) \) y \( h(x) \) no tienen factores comunes.
Sea
\[ f(x) = \dfrac{2}{x - 3} \]El dominio de \( f \) es el conjunto de todos los números reales excepto \( 3 \), ya que este valor hace que el denominador sea cero, y la división por cero no está permitida en matemáticas.
Sin embargo, podemos estudiar cómo se comporta la gráfica de \( f \) cerca de \( x = 3 \).
Evaluemos la función \( f \) en valores de \( x \) cercanos a \( 3 \) tales que \( x < 3 \).
\[ \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x & 1 & 2 & 2.5 & 2.8 & 2.9 & 2.99 & 2.999 & 2.99999 \\ \hline f(x) & -1 & -2 & -4 & -10 & -20 & -200 & -2000 & -2 \times 10^5 \\ \hline \end{array} \]Ahora evaluemos \( f \) para valores de \( x \) cercanos a \( 3 \) tales que \( x > 3 \).
\[ \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x & 5 & 4 & 3.5 & 3.2 & 3.1 & 3.01 & 3.001 & 3.00001 \\ \hline f(x) & 1 & 2 & 4 & 10 & 20 & 200 & 2000 & 2 \times 10^5 \\ \hline \end{array} \]La gráfica de \( f \) se muestra a continuación.

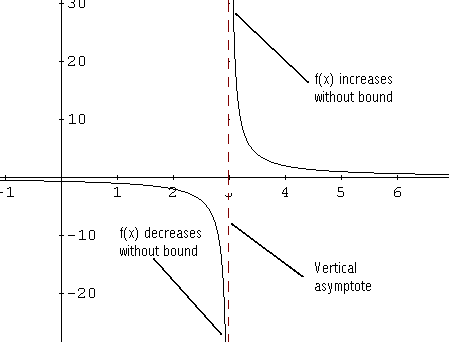
Observa que:
1) Cuando \( x \) se aproxima a 3 por la izquierda (valores menores que 3), \( f(x) \) decrece sin límite.
2) Cuando \( x \) se aproxima a 3 por la derecha (valores mayores que 3), \( f(x) \) crece sin límite.
Decimos que la recta \( x = 3 \), representada como línea discontinua, es una asíntota vertical de la gráfica de \( f \).
En general, la recta \( x = a \) es una asíntota vertical de la gráfica de \( f \) si \( f(x) \) crece o decrece sin límite cuando \( x \) se aproxima a \( a \) por la derecha o por la izquierda.

Sea
\[ f(x) = \dfrac{2x + 1}{x} \]1) Hacemos que \( x \) aumente y calculamos los valores de \( f(x) \).
\[ \begin{array}{|c|c|c|c|c|} \hline x & 1 & 10 & 10^3 & 10^6 \\ \hline f(x) & 3 & 2.1 & 2.001 & 2.000001 \\ \hline \end{array} \]2) Hacemos que \( x \) disminuya y calculamos los valores de \( f(x) \).
\[ \begin{array}{|c|c|c|c|c|} \hline x & -1 & -10 & -10^3 & -10^6 \\ \hline f(x) & 1 & 1.9 & 1.999 & 1.999999 \\ \hline \end{array} \]A medida que \( |x| \) aumenta, el numerador está dominado por el término \( 2x \) y el denominador contiene únicamente el término \( x \).
Por lo tanto, los valores de \( f(x) \) se aproximan a \( 2 \).
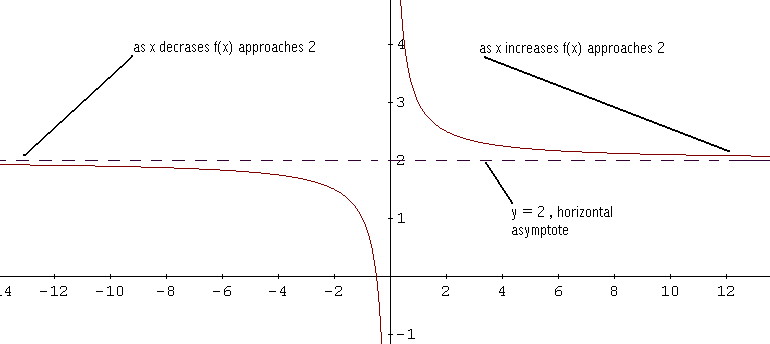
En general, la recta \( y = b \) es una asíntota horizontal de la gráfica de \( f \) si \( f(x) \) se aproxima al valor constante \( b \) cuando \( x \) aumenta o disminuye sin límite.
Sea \( m \) el grado del polinomio del numerador y \( n \) el grado del polinomio del denominador.
Caso 1: Si \( m < n \), la asíntota horizontal es la recta \( y = 0 \).
Caso 2: Si \( m = n \), la asíntota horizontal es la recta \( y = \dfrac{a_m}{b_n} \).
Caso 3: Si \( m > n \), la gráfica no tiene asíntota horizontal.
Sea \( f \) una función racional definida por
\[ f(x) = \dfrac{x + 1}{x - 1} \]a – Encuentre el dominio de \( f \).
b – Encuentre las intersecciones con los ejes \( x \) y \( y \) de la gráfica de \( f \).
c – Encuentre las asíntotas verticales y horizontales de la gráfica de \( f \), si existen.
d – Use sus respuestas de los incisos a, b y c para esbozar la gráfica de la función \( f \).
a – El dominio de \( f \) es el conjunto de todos los números reales excepto \( x = 1 \), ya que este valor de \( x \) hace que el denominador sea cero.
b – La intersección con el eje \( x \) se obtiene resolviendo \( f(x) = 0 \), es decir, \( x + 1 = 0 \). La intersección con el eje \( x \) es el punto \( (-1, 0) \).
La intersección con el eje \( y \) es el punto \( (0, f(0)) = (0, -1) \).
c – La asíntota vertical está dada por el cero del denominador: \( x = 1 \).
El grado del numerador es 1 y el grado del denominador es 1. Como son iguales, y de acuerdo con el teorema anterior, la asíntota horizontal es la recta \( y = \dfrac{1}{1} = 1 \).
d – Aunque los incisos a, b y c proporcionan información importante sobre la gráfica de \( f \), todavía necesitamos construir una tabla de signos para poder esbozar la gráfica con mayor facilidad.
El signo de \( f(x) \) cambia en los ceros del numerador y del denominador. Para construir la tabla de signos, procedemos como al resolver inecuaciones racionales.
Los ceros del numerador y del denominador, que son \( -1 \) y \( 1 \), dividen la recta real en tres intervalos:
\[ (-\infty, -1), \quad (-1, 1), \quad (1, +\infty) \]Seleccionamos un valor de prueba en cada intervalo y determinamos el signo de \( f(x) \).
En el intervalo \( (-\infty, -1) \), elegimos \( -2 \) y calculamos \( f(-2) = \dfrac{-2 + 1}{-2 - 1} = \dfrac{1}{3} > 0 \).
En el intervalo \( (-1, 1) \), elegimos \( 0 \) y calculamos \( f(0) = -1 < 0 \).
En el intervalo \( (1, +\infty) \), elegimos \( 2 \) y calculamos \( f(2) = \dfrac{2 + 1}{2 - 1} = 3 > 0 \).
Coloquemos toda la información sobre la función \( f \) en una tabla.
\[ \begin{array}{|c|c|c|c|c|c|} \hline x & -\infty & -1 & & 1 & +\infty \\ \hline f(x) & + & 0 \ (\text{intersección con } x) & - & \text{A.V.} & + \\ \hline \end{array} \]En la tabla anterior, A.V. significa asíntota vertical.
Para esbozar la gráfica de \( f \), comenzamos trazando las intersecciones con los ejes \( x \) y \( y \), así como las asíntotas vertical y horizontal, utilizando líneas discontinuas. Véase el esquema a continuación.
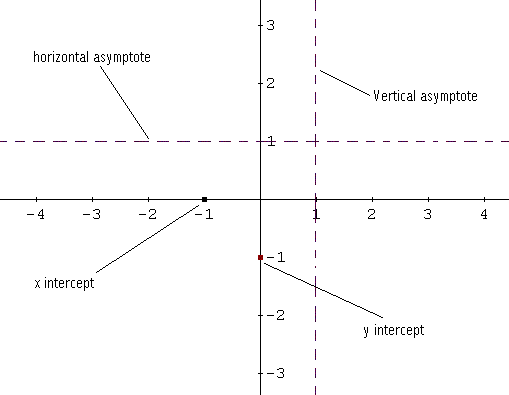
Ahora comenzamos a dibujar la gráfica de \( f \) empezando por la izquierda.
En el intervalo \( (-\infty, -1) \), \( f(x) \) es positiva, por lo que la gráfica está por encima del eje \( x \). Al avanzar desde la izquierda, dibujamos la gráfica teniendo en cuenta que \( y = 1 \) es una asíntota horizontal; la gráfica de \( f \) se aproxima a esta recta.

Entre \( -1 \) y \( 1 \), \( f(x) \) es negativa, por lo que la gráfica está por debajo del eje \( x \). El punto \( (0, -1) \) es una intersección con el eje \( y \) y \( x = 1 \) es una asíntota vertical.
Cuando \( x \) se aproxima a 1 por la izquierda, \( f(x) \) decrece sin límite, ya que \( f(x) < 0 \) en el intervalo \( (-1, 1) \).
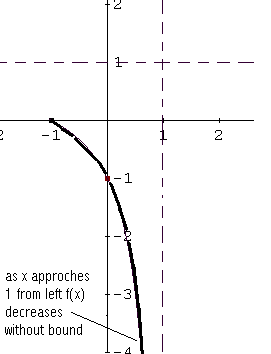
Para \( x > 1 \), \( f(x) > 0 \), por lo que la gráfica está por encima del eje \( x \). Cuando \( x \) se aproxima a 1 por la derecha, la gráfica de \( f \) crece sin límite.
Además, cuando \( x \) aumenta, la gráfica de \( f \) se aproxima a la recta \( y = 1 \), que es la asíntota horizontal.
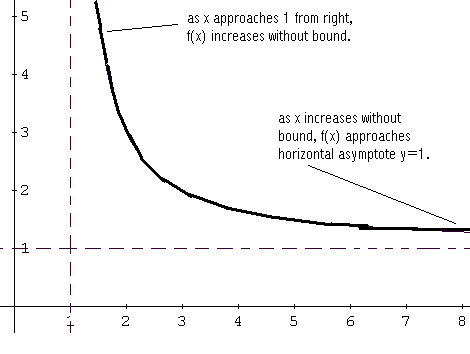
Finalmente, unimos todas las “partes” de la gráfica para obtener la gráfica completa de \( f \).

Sea \( f \) una función racional definida por
\[ f(x) = \dfrac{-x + 2}{x + 4} \]a – Encuentre el dominio de \( f \).
b – Encuentre las intersecciones con los ejes \( x \) y \( y \).
c – Encuentre las asíntotas verticales y horizontales de la gráfica de \( f \), si existen.
d – Use sus respuestas de los incisos a, b y c para esbozar la gráfica de \( f \).
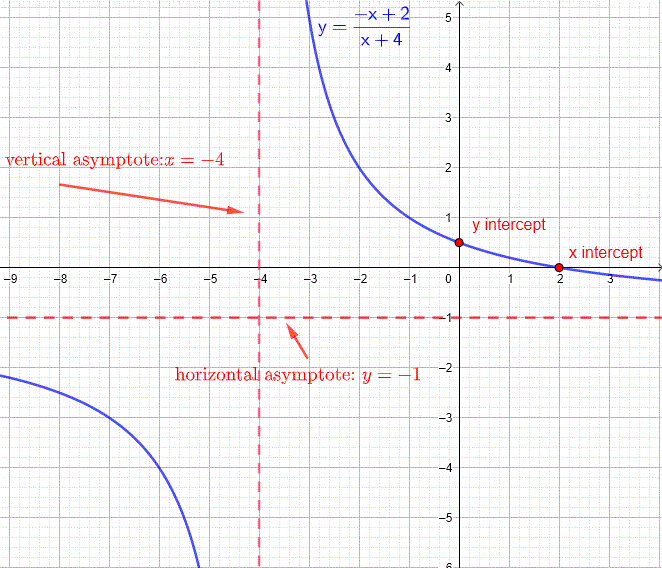
a) Todos los números reales excepto \( x = -4 \).
b) Intersección con el eje \( x \): \( (2, 0) \); intersección con el eje \( y \): \( (0, \tfrac{1}{2}) \).
c) Asíntota vertical: \( x = -4 \); asíntota horizontal: \( y = -1 \).
d) La gráfica se muestra a continuación.