Graficar mediante Traslación, Escalado y Reflexión
Se presenta un tutorial paso a paso sobre las propiedades de las transformaciones, tales como la
traslación vertical y
traslación horizontal, el
escalado
y las reflexiones respecto al
eje x y al
eje y
de las gráficas de funciones.
Traslación / Desplazamiento Horizontal
Para cualquier función \( f(x) \), si reemplazamos \( x \) por \( x + c \), la gráfica de \( f(x + c) \) será la gráfica de \( f(x) \) desplazada horizontalmente \( c \) unidades.
Más específicamente:
\[
f(x + c) \text{ es la gráfica de } f(x) \text{ desplazada } c \text{ unidades hacia la izquierda si } c \gt 0
\]
O equivalentemente:
\[
f(x - c) \text{ es la gráfica de } f(x) \text{ desplazada } c \text{ unidades hacia la derecha si } c \gt 0
\]
El ejemplo de las gráficas de \( f(x) = x^2 \) y \( g(x) = (x - 2)^2 \) se muestra a continuación. Se observa fácilmente que la gráfica de \( (x - 2)^2 \) es la de \( x^2 \) desplazada 2 unidades hacia la derecha.
\[
\begin{array}{c@{\hspace{4cm}}c}
\text{\( f(x) = x^2 \)} \quad & \quad \text{\( g(x) = (x - 2)^2 \)} \\
\end{array}
\]

Si \( c \) es positivo, la gráfica se desplaza hacia la izquierda. El ejemplo de las gráficas de \( f(x) = \sqrt{x} \) y \( g(x) = \sqrt{x + 2} \) se muestra a continuación. Se observa que la gráfica de \( \sqrt{x + 2} \) es la de \( \sqrt{x} \) desplazada 2 unidades hacia la izquierda.
\[
\begin{array}{c@{\hspace{4cm}}c}
\text{\( f(x) = \sqrt{x} \)} \quad & \quad \text{\( g(x) = \sqrt{x + 2} \)} \\
\end{array}
\]

Traslación / Desplazamiento Vertical
Si sumamos una constante \( c \) a \( f(x) \), la gráfica de \( f(x) + c \) será la gráfica de \( f(x) \) trasladada verticalmente.
Si \( c \) es positivo, la gráfica se desplaza hacia arriba.
Si \( c \) es negativo, la gráfica se desplaza hacia abajo, como se muestra a continuación.
\[
\begin{array}{c@{\hspace{3cm}}c}
f(x) = x^2 \quad & \quad g(x) = x^2 + 2
\end{array}
\]

Si \( c \) es negativo, la gráfica se traslada hacia abajo, como se muestra en la siguiente gráfica.
\[
\begin{array}{c@{\hspace{3cm}}c}
f(x) = x^2 \quad & \quad g(x) = x^2 - 1
\end{array}
\]

Reflexión respecto al eje y
Tome cualquier función \( f(x) \) y cambie \( x \) por \( -x \).
La gráfica de \( f(-x) \) será la gráfica de \( f(x) \) reflejada respecto al eje y.
\[
\begin{array}{c c}
f(x) = \sqrt{x} \quad & \quad g(x) = \sqrt{-x}
\end{array}
\]

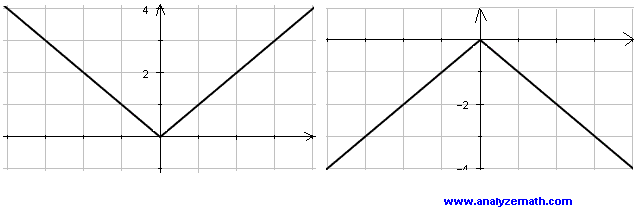
Reflexión respecto al eje x
Tome cualquier función \( f(x) \) y cámbiela por \( -f(x) \).
La gráfica de \( -f(x) \) será la gráfica de \( f(x) \) reflejada respecto al eje x.
\[
\begin{array}{c@{\hspace{3cm}}c}
f(x) = |x| \quad & \quad g(x) = -|x| \\
\end{array}
\]
Escalado Vertical
Tome cualquier función \( f(x) \).
La gráfica de \( kf(x) \) (con \( k \gt 0 \)) será la gráfica de \( f(x) \) estirada verticalmente si \( k \gt 1 \), y comprimida verticalmente si \( 0 < k < 1 \).
La gráfica en azul corresponde a \( f(x) = |x| \) y la gráfica en rojo corresponde a \( g(x) = 2|x| \).

Más Referencias y Enlaces sobre Gráficas
Graficar funciones.







