Este tutorial explica cómo graficar funciones definidas por tramos paso a paso. Analizamos sus gráficas, dominios, rangos y propiedades principales. También puedes usar papel milimetrado gratuito para dibujar las gráficas a mano.
Una función definida por tramos es una función que está definida por diferentes fórmulas en distintos intervalos de su dominio.
El dominio de esta función es el conjunto de todos los números reales, ya que hay una fórmula definida para cada valor de \(x\).
Esta es una función constante definida por tramos. El dominio son todos los números reales excepto \(x = -3\).
Usando la definición del valor absoluto:
\[ f(x) = \begin{cases} x, & x \ge 0 \\ -x, & x < 0 \end{cases} \]El dominio es el conjunto de todos los números reales.
Esta función está definida para todos los números reales.
La función está no definida en el intervalo \((-2, 2]\) y en \(x = 4\).
El dominio es el conjunto de todos los números reales. El rango es: \[ \{-1,\, 2\} \]
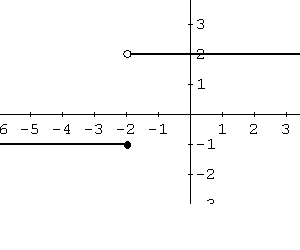
El dominio es el conjunto de todos los números reales y el rango es: \[ (-\infty, +\infty) \]
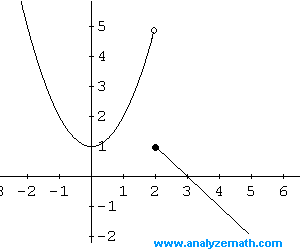
La asíntota horizontal es \(y = 0\).
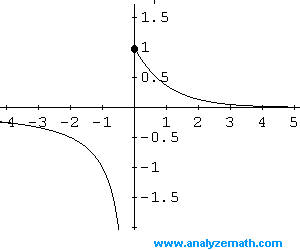
El dominio es el conjunto de todos los números reales y el rango es: \[ \{-1\} \cup [1, +\infty) \]
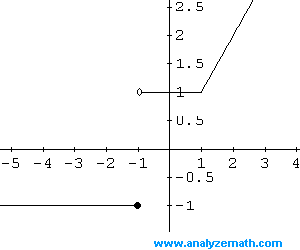
Más referencias: Gráfica de funciones