Problema 1
Cada lado de la pirámide cuadrada que se muestra a continuación mide $10$ pulgadas. La altura inclinada, $H$, de esta pirámide mide $12$ pulgadas.
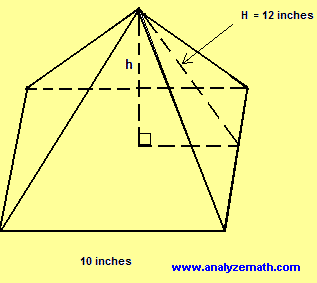
- ¿Cuál es el área, en pulgadas cuadradas, de la base de la pirámide?
- ¿Cuál es el área superficial total, en pulgadas cuadradas, de la pirámide?
- ¿Cuál es $h$, la altura, en pulgadas, de la pirámide?
- Usando la altura que determinaste en la parte (c), ¿cuál es el volumen, en pulgadas cúbicas, de la pirámide?
Ver Solución
a) Área de un cuadrado: $10 \times 10 = 100$ pulgadas cuadradas.
b) Área Total = Base + 4 Triángulos:
$$100 + 4 \left( \frac{1}{2} \times 12 \times 10 \right) = 340 \text{ pulgadas cuadradas.}$$
c) Usando el teorema de Pitágoras con la altura inclinada y la mitad de la base:
$$h = \sqrt{12^2 - 5^2} = \sqrt{119} \text{ pulgadas.}$$
d) Volumen:
$$\text{Volumen} = \frac{1}{3} \times 100 \times \sqrt{119} \approx 363.6 \text{ pulgadas cúbicas.}$$
Problema 2
El paralelogramo que se muestra en la figura a continuación tiene un perímetro de $44$ cm y un área de $64$ cm2. Encuentra el ángulo $T$ en grados.
Ver Solución
Establece la ecuación del perímetro:
$$44 = 2(3x + 2) + 2(5x + 4)$$
Resuelve para $x$:
$$x = 2$$
La longitud de la base es $5(2) + 4 = 14$. El lado inclinado es $3(2) + 2 = 8$.
Encuentra la altura del paralelogramo usando el área:
$$\text{altura} = \frac{\text{área}}{\text{base}} = \frac{64}{14} = \frac{32}{7} \text{ cm}$$
Usa trigonometría para encontrar el ángulo $T$:
$$\sin(T) = \frac{\text{Opuesto}}{\text{Hipotenusa}} = \frac{32/7}{8} = \frac{32}{56} = \frac{4}{7}$$
$$T = \arcsin\left(\frac{4}{7}\right) \approx 34.8^\circ$$
Problema 3
Encuentra el área del cuadrilátero que se muestra en la figura. (NOTA: la figura no está dibujada a escala)
Ver Solución
El triángulo $\triangle ABD$ es un triángulo rectángulo; por lo tanto, por el teorema de Pitágoras:
$$BD^2 = 15^2 + 15^2 = 450$$
Para el triángulo $\triangle BCD$, prueba si es un triángulo rectángulo verificando la suma de los cuadrados de sus lados más cortos:
$$BC^2 + CD^2 = 21^2 + 3^2 = 441 + 9 = 450$$
Dado que $BC^2 + CD^2 = BD^2$, el triángulo $\triangle BCD$ también es un triángulo rectángulo.
El área total del cuadrilátero es la suma de las áreas de los dos triángulos rectángulos:
$$\text{Área} = \left(\frac{1}{2} \times 15 \times 15\right) + \left(\frac{1}{2} \times 21 \times 3\right) = 112.5 + 31.5 = 144$$
Problema 4
En la figura a continuación, el triángulo OAB tiene un área de $72$ unidades cuadradas y el triángulo ODC tiene un área de $288$ unidades cuadradas. Encuentra $x$ como la longitud del segmento BC e $y$ como la longitud del segmento AD.
Ver Solución
Usando la fórmula del seno para el área de un triángulo, evalúa $\triangle OAB$:
$$\text{Área del } \triangle OAB = 72 = \frac{1}{2} \sin(\angle AOB) \cdot OA \cdot OB$$
Dado que $OA = 18$ y $OB = 16$, resuelve para $\sin(\angle AOB)$:
$$\sin(\angle AOB) = \frac{2 \cdot 72}{18 \cdot 16} = \frac{1}{2}$$
Dado que $\angle DOC$ y $\angle AOB$ son ángulos opuestos por el vértice, $\sin(\angle DOC) = \sin(\angle AOB) = \frac{1}{2}$.
Ahora evalúa el área del $\triangle ODC$:
$$\text{Área del } \triangle ODC = 288 = \frac{1}{2} \sin(\angle DOC) \cdot OD \cdot OC$$
$$288 = \frac{1}{2} \left(\frac{1}{2}\right) \cdot (18 + y)(16 + x)$$
$$1152 = (18 + y)(16 + x)$$
Los puntos A, B, C y D se encuentran en un círculo. Por el Teorema de las Secantes Intersecantes:
$$OA \cdot OD = OB \cdot OC$$
$$18(18 + y) = 16(16 + x)$$
Ahora tenemos un sistema de ecuaciones:
1) $(18 + y)(16 + x) = 1152$
2) $18(18 + y) = 16(16 + x) \Rightarrow (18 + y) = \frac{8}{9}(16 + x)$
Sustituye la ecuación 2 en la ecuación 1:
$$\left(\frac{8}{9}(16 + x)\right)(16 + x) = 1152$$
$$(16 + x)^2 = 1152 \times \frac{9}{8} = 1296$$
$$16 + x = 36 \Rightarrow x = 20$$
Sustituye $x = 20$ de nuevo en la ecuación 2:
$$18 + y = \frac{8}{9}(16 + 20) = \frac{8}{9}(36) = 32$$
$$y = 14$$
Problema 5
Encuentra las dimensiones del rectángulo que tiene una longitud $3$ metros mayor que su ancho y un perímetro igual en valor a su área.
Ver Solución
Sea $L$ la longitud y $W$ el ancho del rectángulo. Dado: $L = W + 3$
Perímetro: $2L + 2W = 2(W + 3) + 2W = 4W + 6$
Área: $LW = (W + 3)W = W^2 + 3W$
Dado que el área y el perímetro son iguales en valor:
$$W^2 + 3W = 4W + 6$$
Resuelve la ecuación cuadrática:
$$W^2 - W - 6 = 0$$
$$(W - 3)(W + 2) = 0$$
El ancho no puede ser negativo, así que $W = 3$. Sustituye para encontrar la longitud:
$$L = 3 + 3 = 6$$
Respuesta: Ancho = $3$ metros, Longitud = $6$ metros.
Problema 6
Encuentra la circunferencia de un disco circular cuya área es $100 \pi$ centímetros cuadrados.
Ver Solución
Sea $r$ el radio del disco. El área es $100\pi$; por lo tanto,
$$100\pi = \pi r^2$$
Resuelve para $r$:
$$r = 10$$
La circunferencia es:
$$C = 2\pi r = 20\pi \text{ cm}$$
Problema 7
Un semicírculo de área $1250 \pi$ centímetros cuadrados está inscrito dentro de un rectángulo. El diámetro del semicírculo coincide con la longitud del rectángulo. Encuentra el área del rectángulo.
Ver Solución
Sea $r$ el radio del semicírculo. El área es:
$$1250\pi = \frac{1}{2} \pi r^2$$
Resolviendo para $r$:
$$2500 = r^2 \Rightarrow r = 50$$
La longitud del rectángulo es $2r = 100$ (ya que el semicírculo está inscrito).
El ancho del rectángulo es $r = 50$ (ya que el semicírculo está inscrito).
El área del rectángulo es:
$$\text{Área} = 100 \times 50 = 5000 \text{ cm}^2$$