Problema 1
Encuentre $x$ y $H$ en el triángulo rectángulo de abajo.
Ver solución
$$ x = \frac{10}{\tan(51^\circ)} = 8.1 \; \text{ (2 cifras significativas)} $$
$$ H = \frac{10}{\sin(51^\circ)} = 13 \; \text{ (2 cifras significativas) } $$
Problema 2
Encuentre las longitudes de todos los lados del triángulo rectángulo de abajo si su área es 400.
Ver solución
El área viene dada por:
$$ \frac{1}{2}(2x)(x) = 400 $$
Resuelva para $x$:
$$ x = 20, \quad 2x = 40 $$
Use el teorema de Pitágoras:
$$ (2x)^2 + (x)^2 = H^2 $$
Resuelva para $H$:
$$ H = x \sqrt{5} = 20 \sqrt{5} $$
Problema 3
$BH$ es perpendicular a $AC$. Encuentre $x$, la longitud de $BC$.
Ver solución
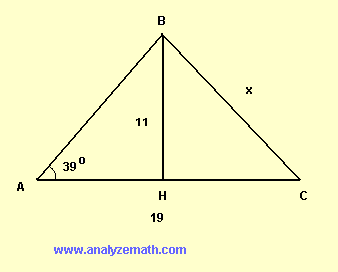
$BH$ perpendicular a $AC$ significa que los triángulos $\triangle ABH$ y $\triangle HBC$ son triángulos rectángulos. Por lo tanto:
$$ \tan(39^\circ) = \frac{11}{AH} \quad \Rightarrow \quad AH = \frac{11}{\tan(39^\circ)} $$
$$ HC = 19 - AH = 19 - \frac{11}{\tan(39^\circ)} $$
Aplique el teorema de Pitágoras al triángulo $\triangle HBC$:
$$ 11^2 + HC^2 = x^2 $$
Sustituya $HC$ y resuelva para $x$:
$$ x = \sqrt{11^2 + \left(19 - \frac{11}{\tan(39^\circ)}\right)^2} $$
$$ x \approx 12.3 \quad \text{(redondeado a 3 cifras significativas)} $$
Problema 4
ABC es un triángulo rectángulo con un ángulo recto en $A$. Encuentre $x$, la longitud de $DC$.
Ver solución
Dado que $\angle A$ es recto, ambos triángulos $\triangle ABC$ y $\triangle ABD$ son rectángulos, y por lo tanto podemos aplicar el teorema de Pitágoras:
$$ 14^2 = 10^2 + AD^2, \quad 16^2 = 10^2 + AC^2 $$
Resuelva para $AD$ y $AC$:
$$ AD = \sqrt{14^2-10^2}, \quad AC = \sqrt{16^2 - 10^2} $$
Además, $x = AC - AD$:
$$ x = \sqrt{16^2 - 10^2} - \sqrt{14^2 - 10^2} $$
$$ x \approx 2.69 \quad \text{(redondeado a 3 cifras significativas)} $$
Problema 5
En la figura de abajo, $AB$ y $CD$ son perpendiculares a $BC$, y el tamaño del ángulo $\angle ACB$ es $31^\circ$. Encuentre la longitud del segmento $BD$.
Ver solución
Use el triángulo rectángulo $\triangle ABC$ para escribir:
$$ \tan(31^\circ) = \frac{6}{BC} \quad \Rightarrow \quad BC = \frac{6}{\tan(31^\circ)} $$
Use el teorema de Pitágoras en el triángulo rectángulo $\triangle BCD$ para escribir:
$$ 9^2 + BC^2 = BD^2 $$
Resuelva para $BD$ y sustituya $BC$:
$$ BD = \sqrt{9^2 + \left( \frac{6}{\tan(31^\circ)} \right)^2} $$
$$ BD \approx 13.4 \quad \text{(redondeado a 3 cifras significativas)} $$
Problema 6
El área de un triángulo rectángulo es 50. Uno de sus ángulos es $45^\circ$. Encuentre las longitudes de los lados y la hipotenusa del triángulo.
Ver solución
El triángulo es rectángulo y uno de sus ángulos es $45^\circ$. El tercer ángulo también es $45^\circ$, y por lo tanto el triángulo es rectángulo e isósceles.
Sea $x$ la longitud de uno de los catetos, y $H$ la hipotenusa.
$$ \text{Área} = \frac{1}{2}x^2 = 50 \quad \Rightarrow \quad x = 10 $$
Use el teorema de Pitágoras:
$$ x^2 + x^2 = H^2 $$
$$ \Rightarrow \quad H = 10\sqrt{2} $$
Problema 7
En un triángulo rectángulo $\triangle ABC$, $\tan(A) = \frac{3}{4}$. Encuentre $\sin(A)$ y $\cos(A)$.
Ver solución
Sea $a$ la longitud del lado opuesto al ángulo $A$, $b$ la longitud del lado adyacente al ángulo $A$ y $h$ la longitud de la hipotenusa.
$$ \tan(A) = \frac{\text{lado opuesto}}{\text{lado adyacente}} = \frac{a}{b} = \frac{3}{4} $$
Podemos escribir que: $a = 3k$ y $b = 4k$, donde $k$ es un coeficiente de proporcionalidad.
Encontremos $h$. Usando el teorema de Pitágoras, escribimos:
$$ h^2 = (3k)^2 + (4k)^2 $$
$$ h^2 = 9k^2 + 16k^2 = 25k^2 \quad \Rightarrow \quad h = 5k $$
$$ \sin(A) = \frac{a}{h} = \frac{3k}{5k} = \frac{3}{5}, \quad \cos(A) = \frac{b}{h} = \frac{4k}{5k} = \frac{4}{5} $$
Problema 8
En un triángulo rectángulo $\triangle ABC$ con ángulo $A = 90^\circ$, encuentre los ángulos $B$ y $C$ tales que $\sin(B) = \cos(B)$.
Ver solución
Sea $b$ la longitud del lado opuesto al ángulo $B$, $c$ la longitud del lado opuesto al ángulo $C$, y $h$ la hipotenusa.
$$ \sin(B) = \frac{b}{h}, \quad \cos(B) = \frac{c}{h} $$
$$ \sin(B) = \cos(B) \quad \Rightarrow \quad \frac{b}{h} = \frac{c}{h} \quad \Rightarrow \quad b = c $$
Dado que los dos lados son iguales en longitud, el triángulo es isósceles, y los ángulos $B$ y $C$ son iguales, cada uno midiendo $45^\circ$.
Problema 9
Un rectángulo tiene dimensiones de 10 cm por 5 cm. Determine las medidas de los ángulos en el punto donde se intersectan las diagonales.
Ver solución
El diagrama de abajo muestra un rectángulo con diagonales y la mitad de uno de los ángulos etiquetada como $x$.
$$ \tan(x) = \frac{5}{2.5} = 2 \quad \Rightarrow \quad x = \arctan(2) $$
El ángulo mayor formado por las diagonales es $2x$:
$$ 2x = 2 \arctan(2) \approx 127^\circ \quad \text{(3 cifras significativas)} $$
$$ \text{Ángulo menor formado por las diagonales: } 180^\circ - 2x \approx 53^\circ $$
Problema 10
Las longitudes del lado AB y del lado BC de un triángulo escaleno ABC son 12 cm y 8 cm respectivamente. El tamaño del ángulo C es $59^\circ$. Encuentre la longitud del lado AC.
Ver solución
Sea $x$ la longitud del lado AC. Use la ley del coseno:
$$ 12^2 = 8^2 + x^2 - 2 \cdot 8 \cdot x \cdot \cos(59^\circ) $$
Resuelva la ecuación cuadrática para $x$:
$$ x = 14.0 \quad \text{y} \quad x = -5.7 $$
Dado que $x$ no puede ser negativo, la solución es:
$$ x = 14.0 \quad \text{(redondeado a un decimal)} $$
Problema 11
Desde la cima de un edificio de 200 metros de altura, el ángulo de depresión hacia la base de un segundo edificio es de 20 grados. Desde el mismo punto, el ángulo de elevación hacia la cima del segundo edificio es de 10 grados. Calcule la altura del segundo edificio.
Ver solución
$$ \tan(20^\circ) = \frac{200}{L} \quad \Rightarrow \quad L = \frac{200}{\tan(20^\circ)} $$
$$ \tan(10^\circ) = \frac{H_2}{L} \quad \Rightarrow \quad H_2 = L \cdot \tan(10^\circ) $$
$$ = \frac{200 \cdot \tan(10^\circ)}{\tan(20^\circ)} $$
$$ \text{Altura del segundo edificio} = 200 + H_2 = 200 + \frac{200 \cdot \tan(10^\circ)}{\tan(20^\circ)} \approx 297 \text{ metros} $$
Problema 12
Karla está ascendiendo verticalmente en un globo aerostático, directamente sobre un punto P en el suelo. Karla observa un automóvil estacionado en el suelo con un ángulo de depresión de $30^\circ$. El globo asciende 50 metros. Ahora el ángulo de depresión hacia el automóvil es de $35^\circ$. ¿A qué distancia está el automóvil del punto P?
Ver solución
Sea $h$ la altura inicial del globo sobre el punto $P$. Después de ascender, la nueva altura es $h + 50$ metros.
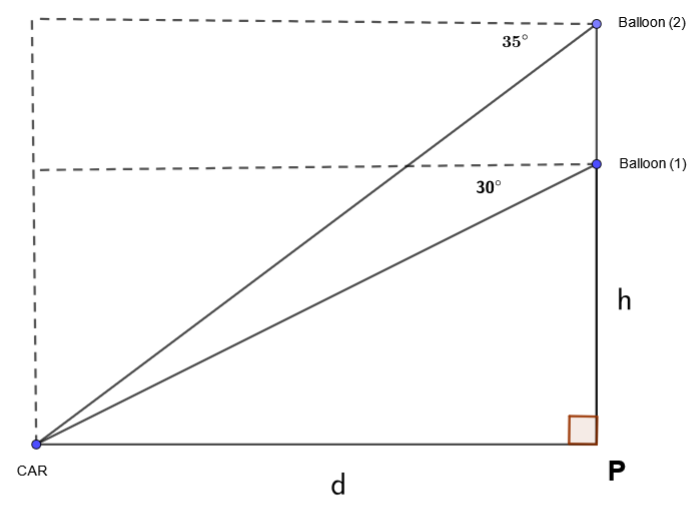La distancia horizontal desde el automóvil hasta $P$ es $d$ (que permanece constante).
El ángulo de depresión desde el globo hasta el automóvil es igual al ángulo de elevación desde el automóvil hasta el globo (por ángulos alternos internos).
Entonces, para la posición inicial:
$$ \tan(30^\circ) = \frac{h}{d} $$
$$ \frac{1}{\sqrt{3}} = \frac{h}{d} \quad \text{(ya que } \tan(30^\circ) = \frac{1}{\sqrt{3}} \text{)} $$
Por lo tanto,
$$ h = \frac{d}{\sqrt{3}} \tag{1} $$
Después de ascender 50 metros, la nueva altura es $h + 50$, y el ángulo de depresión es $35^\circ$:
$$ \tan(35^\circ) = \frac{h + 50}{d} $$
Entonces,
$$ h + 50 = d \cdot \tan(35^\circ) \tag{2} $$
Ahora sustituya la ecuación (1) en la ecuación (2):
$$ \frac{d}{\sqrt{3}} + 50 = d \cdot \tan(35^\circ) $$
Reorganice para resolver para $d$:
$$ 50 = d \cdot \tan(35^\circ) - \frac{d}{\sqrt{3}} $$
$$ 50 = d \left( \tan(35^\circ) - \frac{1}{\sqrt{3}} \right) $$
$$ d = \frac{50}{\tan(35^\circ) - \frac{1}{\sqrt{3}}} $$
Use los valores numéricos: $\tan(35^\circ) \approx 0.7002$ y $\frac{1}{\sqrt{3}} \approx 0.57735$ para obtener:
$$ d = \frac{50}{0.7002 - 0.57735} = \frac{50}{0.12285} \approx 406.97 $$
Por lo tanto, el automóvil está aproximadamente a $407$ metros del punto $P$.
Problema 13
Si la sombra de un edificio aumenta 10 metros cuando el ángulo de elevación de los rayos del sol disminuye de $70^\circ$ a $60^\circ$, ¿cuál es la altura del edificio?
Ver solución
Sea $h$ la altura del edificio. Inicialmente, cuando el ángulo de elevación es de $70^\circ$, la longitud de la sombra es $s$.
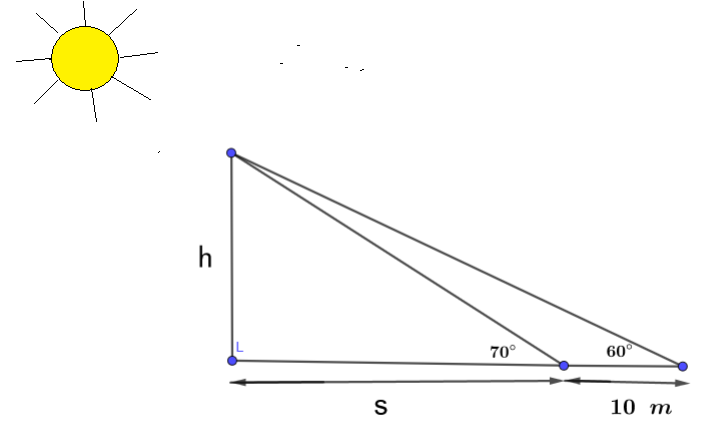
Cuando el ángulo de elevación disminuye a $60^\circ$, la longitud de la sombra se convierte en $s + 10$.
Para el caso inicial (ángulo $70^\circ$):
$$ \tan(70^\circ) = \frac{h}{s} $$
Por lo tanto,
$$ s = \frac{h}{\tan(70^\circ)} \tag{1} $$
Para el nuevo caso (ángulo $60^\circ$):
$$ \tan(60^\circ) = \frac{h}{s + 10} $$
Por lo tanto,
$$ s + 10 = \frac{h}{\tan(60^\circ)} \tag{2} $$
Ahora, reste la ecuación (1) de la ecuación (2):
$$ (s + 10) - s = \frac{h}{\tan(60^\circ)} - \frac{h}{\tan(70^\circ)} $$
$$ 10 = h \left( \frac{1}{\tan(60^\circ)} - \frac{1}{\tan(70^\circ)} \right) $$
Por lo tanto,
$$ h = \frac{10}{ \frac{1}{\tan(60^\circ)} - \frac{1}{\tan(70^\circ)} } $$
Simplifique la expresión:
$$ h = \frac{10}{ \cot(60^\circ) - \cot(70^\circ) } $$
Evalúe numéricamente:
$$ h \approx 46.86474 $$
Por lo tanto, la altura del edificio es de aproximadamente $46.9$ metros.