Problemas de Geometría con Soluciones y Respuestas

Resuelva la ecuación lineal \( x - y = 1 \) para \( x \): \( x = 1 + y \)

Sustituya en la ecuación estándar del círculo dado: \[ (1 + y)^2 + 2(1 + y) + y^2 + 4y = -1 \]

Expanda y simplifique la expresión. Combine términos semejantes y reescriba la ecuación cuadrática resultante en forma estándar: \[ 2y^2 + 8y + 4 = 0 \]

Resuelva la ecuación cuadrática para obtener los valores de \( y \): \[ y = -2 \pm \sqrt{2} \]

Use la sustitución \( x = 1 + y \) para encontrar los valores de \( x \) correspondientes.

Por lo tanto, los puntos de intersección entre la línea y el círculo son: \[ (-1 + \sqrt{2},\ -2 + \sqrt{2}) \quad \text{y} \quad (-1 - \sqrt{2},\ -2 - \sqrt{2}) \]

Para encontrar el área del triángulo formado por las líneas \( y = x \) y \( y = -2x + 3 \), primero grafique ambas líneas.

Resuelva el sistema de ecuaciones para encontrar el punto de intersección: \[ y = x \quad \text{y} \quad y = -2x + 3 \]

Resolviendo, encontramos que el punto de intersección es \( (1,\ 1) \). La altura del triángulo es 1 (la coordenada y).

La intersección en x de \( y = -2x + 3 \) se encuentra estableciendo \( y = 0 \): \[ 0 = -2x + 3 \Rightarrow x = \dfrac{3}{2} \]

La base del triángulo es \( \dfrac{3}{2} \). Entonces, el área es: \[ \text{Área} = \dfrac{1}{2} \times \text{base} \times \text{altura} = \dfrac{1}{2} \times \dfrac{3}{2} \times 1 = \dfrac{3}{4} \]

La fórmula del seno para el área de un triángulo usando dos lados y el ángulo incluido se puede escribir como: \[ 18 = \dfrac{1}{2} \times 5 \times 10 \times \sin(A) \]

Resolviendo para \( \sin(A) \), obtenemos: \[ \sin(A) = \dfrac{18}{25} \]

Ahora usamos la ley del coseno para encontrar la longitud \( x \) del tercer lado opuesto al ángulo \( A \): \[ x^2 = 5^2 + 10^2 - 2 \times 5 \times 10 \times \cos(A) \]

Dado que \( \cos(A) = \sqrt{1 - \sin^2(A)} \), sustituimos: \[ \cos(A) = \sqrt{1 - \left(\dfrac{18}{25}\right)^2} \]

Sustituya \( \cos(A) \) en la expresión de la ley del coseno y resuelva para \( x \): \[ x \approx 7.46 \quad \text{(redondeado a 3 dígitos significativos)} \]

El área del triángulo BOC es 15 y está dada por \[ \text{Área}_{\triangle BOC} = \dfrac{1}{2} \cdot BO \cdot OC \cdot \sin(\angle BOC) \]

El área del triángulo AOD está dada por \[ \text{Área}_{\triangle AOD} = \dfrac{1}{2} \cdot AO \cdot OD \cdot \sin(\angle AOD) \]

Nótese que los ángulos \( \angle BOC \) y \( \angle AOD \) son iguales.

Por el teorema de las cuerdas intersectantes, tenemos: \[ AO \cdot OC = BO \cdot OD \]

Esto se puede escribir como: \[ \dfrac{AO}{BO} = \dfrac{OD}{OC} = \dfrac{10}{5} = 2 \]

Las razones \( \dfrac{AO}{BO} \) y \( \dfrac{OD}{OC} \) son ambas iguales a 2, por lo tanto su producto es: \[ \dfrac{AO \cdot OD}{BO \cdot OC} = 4 \]

Lo que da: \[ AO \cdot OD = 4 \cdot (BO \cdot OC) \]

Por lo tanto, el área del triángulo AOD es 4 veces el área del triángulo BOC: \[ \text{Área}_{\triangle AOD} = 4 \cdot 15 = 60 \]

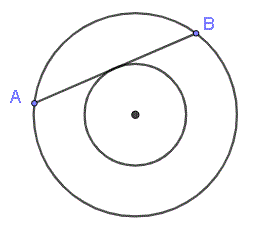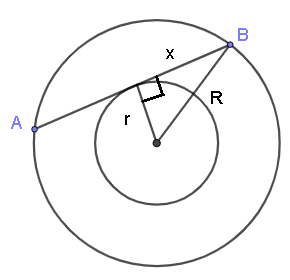
Si dibujamos un radio en el círculo pequeño hasta el punto de tangencia, este será perpendicular a la cuerda (ver figura siguiente). Si \( x \) es la mitad de la longitud de \( AB \), \( r \) es el radio del círculo pequeño y \( R \) es el radio del círculo grande, entonces por el Teorema de Pitágoras, tenemos: \[ r^2 + x^2 = R^2 \] \[ 6^2 + x^2 = 10^2 \]

Resuelva para \( x \): \( x = 8 \)

Longitud de \( AB = 2x = 16 \)

Use la ley del coseno en el triángulo ABE: \[ 13^2 = 20^2 + 9^2 - 2(20)(9)\cos(T) \tag{I} \]

Use la ley del coseno en el triángulo ACB:

\[ x^2 = 20^2 + 9^2 - 2(20)(9)\cos(90^\circ - T) \]

Note que \( \cos(90^\circ - T) = \sin(T) \) y reescriba la segunda ecuación como:

\[ x^2 = 20^2 + 9^2 - 2(20)(9)\sin(T) \tag{III} \]

Resuelva la ecuación (I) para \( \cos(T) \):

\[ \cos(T) = \dfrac{13}{15} \]

Use la identidad trigonométrica \( \sin(T) = \sqrt{1 - \cos^2(T)} \) para encontrar: \[ \sin(T) = \dfrac{2\sqrt{14}}{15} \]

Sustituya \( \sin(T) = \dfrac{2\sqrt{14}}{15} \) en la ecuación (III) y resuelva para \( x \):

\[ x = \sqrt{481 - 48\sqrt{14}} \approx 17.4 \]

(Aproximado a 3 dígitos significativos.)

a) Volumen del Sólido Compuesto

1. Volumen del cilindro: \[ V_{\text{cilindro}} = \pi r^2 h = \pi (5)^2 (12) = 300\pi \, \text{cm}^3 \]

2. Volumen del hemisferio: \[ V_{\text{hemisferio}} = \frac{1}{2} \left( \frac{4}{3} \pi r^3 \right) = \frac{2}{3} \pi (5)^3 = \frac{250}{3} \pi \, \text{cm}^3 \]

3. Volumen total: \[ V_{\text{total}} = V_{\text{cilindro}} + V_{\text{hemisferio}} = 300\pi + \frac{250}{3}\pi = \frac{1150}{3} \pi \, \text{cm}^3 \]

b) Masa del Objeto \[ \text{Masa} = \text{Densidad} \times \text{Volumen} = 7.8 \times \frac{1150}{3} \pi \]

Aproximando usando \( \pi \approx 3.1416 \): \[ \text{Masa} \approx 7.8 \times \frac{1150}{3} \times 3.1416 \approx 9396.66 \, \text{g} \]

a) Área del Jardín

1. Área del rectángulo: \[ A_{\text{rect}} = \text{largo} \times \text{ancho} = 12 \times 8 = 96 \, \text{m}^2 \]

2. Área del semicírculo (con radio \( r = 4 \) metros): \[ A_{\text{semi}} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (4)^2 = 8\pi \, \text{m}^2 \]

3. Área total: \[ A_{\text{total}} = A_{\text{rect}} + A_{\text{semi}} = 96 + 8\pi \, \text{m}^2 \]

Usando \( \pi \approx 3.1416 \): \[ A_{\text{total}} \approx 96 + 8(3.1416) = 121.13 \, \text{m}^2 \]

b) Perímetro del Jardín

Nota: Excluimos el borde compartido entre el semicírculo y el rectángulo.

1. Tres lados del rectángulo (excluyendo el lado de 8 m): \[ P_{\text{rect}} = 12 + 8 + 12 = 32 \, \text{m} \]

2. Parte curva del semicírculo: \[ P_{\text{semi}} = \frac{1}{2} (2\pi r) = \pi r = \pi \cdot 4 = 4\pi \, \text{m} \]

3. Perímetro total: \[ P_{\text{total}} = 32 + 4\pi \approx 32 + 12.566 = 44.57 \, \text{m} \]