
Se introducen los vectores 3D junto con operaciones como la suma, diferencia y multiplicación escalar. También se incluyen propiedades como la magnitud. Se incluyen preguntas con soluciones detalladas.
Un vector es una cantidad que tiene tanto magnitud como dirección. Se representa geométricamente por un segmento de recta cuya longitud es la magnitud y una flecha que indica su dirección, como se muestra en la figura. Los vectores se usan en física para modelar cantidades con tamaño y dirección como velocidades, fuerzas, aceleraciones; en ingeniería, química, gráficos por computadora, robótica y muchos otros campos.

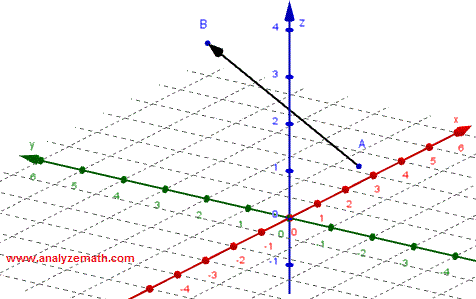
En la figura, el vector se define usando un punto inicial A y un punto terminal B. Por lo tanto, el vector puede denotarse como \( \vec{AB} \).
Los vectores con magnitudes iguales y misma dirección son vectores equivalentes.

Dados dos vectores \( \vec{v_1} \) y \( \vec{v_2} \), su suma es un vector obtenido al posicionar primero el vector \( \vec{v_2} \) de modo que su punto inicial coincida con el punto terminal de \( \vec{v_1} \). La suma \( \vec{v_1} + \vec{v_2} \) es el vector cuyo punto inicial es el de \( \vec{v_1} \) y su punto terminal es el de \( \vec{v_2} \). Nota: \( \vec{v_1} + \vec{v_2} = \vec{v_2} + \vec{v_1} \). Además, la suma de dos vectores coincide con la diagonal del paralelogramo determinado por \( \vec{v_1} \) y \( \vec{v_2} \).

Dados dos vectores \( \vec{v_1} \) y \( \vec{v_2} \), la diferencia \( \vec{v_2} - \vec{v_1} \) puede definirse como la suma \( \vec{v_2} + (- \vec{v_1}) \) y se representa geométricamente como se muestra.

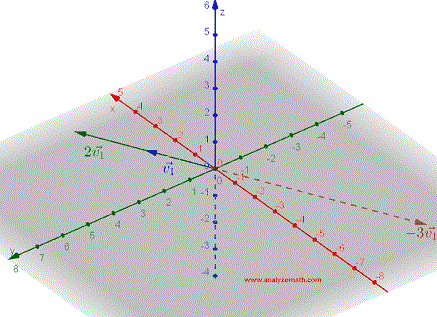
Un vector \( \vec{v_1} \) multiplicado por un escalar \( k \) se define como un vector \( k\vec{v_1} \) paralelo a \( \vec{v_1} \) y cuya dirección es la misma que la de \( \vec{v_1} \) si \( k > 0 \) y opuesta si \( k < 0 \). La magnitud (longitud) de \( k\vec{v_1} \) es \( | k | \) veces la magnitud de \( \vec{v_1} \). La figura muestra vectores \( \vec{v_1} \), \( 2\vec{v_1} \) y \( -3 \vec{v_1} \).
Un vector unitario es un vector con magnitud igual a 1. A continuación se muestra un sistema de coordenadas rectangular 3D con vectores unitarios \(\vec{i} \), \(\vec{j} \) y \(\vec{k} \) en la dirección positiva de los ejes x, y y z respectivamente. Los vectores \(\vec{i} \), \(\vec{j} \) y \(\vec{k} \) pueden definirse por sus componentes de la siguiente manera:
\(\vec{i} = \lt 1 , 0 , 0 >\), una unidad a lo largo del eje x.
\(\vec{j} = \lt 0,1,0> \), una unidad a lo largo del eje y.
\(\vec{k} = \lt 0 ,0,1> \), una unidad a lo largo del eje z.

Las componentes de cualquier vector \(\vec{v} \) se definen expresando \(\vec{v} \) como una suma de múltiplos de los vectores unitarios \(\vec{i} \), \(\vec{j} \) y \(\vec{k} \) de la siguiente manera: \[ \vec{v} = 3\vec{i} + 4\vec{j} + 5\vec{k}\] o en forma de componentes como: \[ \vec{v} = \lt 3,4,5> \]

Las componentes de un vector \(\vec{v} \) definido por su punto inicial \( A = (x_1 , y_1 ,z_1)\) y su punto terminal \( B = (x_2 , y_2 ,z_2) \) vienen dadas por: \[ \vec{v} = \lt x_2-x_1,y_2-y_1,z_2-z_1> \]
Dado el vector \( \vec{v} = \lt a,b,c> \), su magnitud (o longitud) viene dada por: \[ ||\vec{v}|| = \sqrt{a^2+b^2+c^2} \] El vector unitario \( \vec{u} \), definido como un vector de magnitud igual a 1, en la misma dirección que \( \vec{v} \) viene dado por: \[ u = \dfrac{1}{||\vec{v}||} \vec{v} \]
Dados los vectores \( \vec{v_1} = \lt a_1,b_1,c_1> \) y \( \vec{v_2} = \lt a_2,b_2,c_2> \), la suma \( \vec{v_1} + \vec{v_2}\), la diferencia \( \vec{v_1} - \vec{v_2}\) y la multiplicación escalar \( k \vec{v_1} \), donde k es un número real, vienen dadas por: \[ \vec{v_1} + \vec{v_2} = \lt a_1+a_2,b_1+b_2,c_1+c_2> \] \[ \vec{v_1} - \vec{v_2} = \lt a_1 - a_2,b_1 - b_2,c_1 - c_2> \] \[ k \vec{v_1} = \lt k a_1,k b_1,k c_1> \]
Se incluyen soluciones y explicaciones detalladas a las siguientes preguntas.
1) Encuentra las componentes de los vectores \( \vec{AB} \) y \( \vec{BA}\) donde A y B son puntos dados por sus coordenadas A(2,6,7) y B(0,-3,1) y muestra que \( \vec{AB} = -1 \vec{BA}\).
2) Dados los vectores \(\vec{v_1} = \lt 0,-3,2>\) y \( \vec{v_2} = \lt-3,4,5> \), encuentra:
3) Dado el vector \(\vec{v} = \lt 0,-3,2>\), encuentra el vector unitario en la misma dirección que \(\vec{v} \) y verifica que su magnitud es igual a 1.
4) Dados los puntos A(2,6,7), B(0,-3,1) y C(0,3,4), encuentra las componentes de los vectores \( \vec{AB} \), \( \vec{AC}\) y \( \vec{BC}\) y muestra que \( \vec{AB} + \vec{BC} = \vec{AC}\).
5) Dados los puntos A(-1,2,1), B(2,4,2) y C(5,6,3), encuentra las componentes de los vectores \( \vec{AB} \), \( \vec{BC}\) y \( \vec{AC}\) y determina cuáles de estos vectores son equivalentes y cuáles son paralelos.
6) Dados los vectores \(\vec{v_1} = \lt -4,0,2>\) y \( \vec{v_2} = \lt -1,-4,2> \), encuentra el vector \( \vec{v} \) tal que \(\vec{v_1} - 2 \vec{v} = 3 \vec{v} - 3 \vec{v_2} \).
7) Encuentra un vector en la misma dirección que el vector \( \vec{v} = \lt-4,2,2> \) pero con el doble de longitud.
8) Encuentra un vector en dirección opuesta al vector \( \vec{v} = \lt -1,2,2> \) pero con una longitud de 5 unidades.
9) Dado el vector \( \vec{v} = \lt -1,2,2> \), encuentra un número real \( k \) tal que \( ||k \vec{v} || = 1/5 \).
10) Encuentra \( b \) y \( c \) tales que los vectores \(\vec{v_1} = \lt -4,6,2>\) y \( \vec{v_2} = \lt 2,b,c> \) sean paralelos.
11) ¿Son colineales los tres puntos A(2,6,7), B(1,4,5) y C(0,2,3)?
12) Se muestra un cubo de lado 2 unidades.
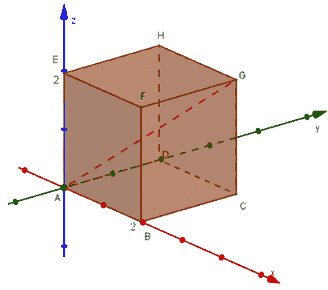
Soluciones y explicaciones detalladas a estas preguntas.