Problemas y Preguntas de Álgebra con Soluciones - Grado 12

Reescribimos las expresiones dadas a la misma potencia y las comparamos: \[ 25^{100} \] \[ 2^{300} = (2^3)^{100} = 8^{100} \] \[ 3^{400} = (3^4)^{100} = 81^{100} \] \[ 4^{200} = (4^2)^{100} = 16^{100} \] \[ 2^{600} = (2^6)^{100} = 64^{100} \] Ahora, las ordenamos de mayor a menor: \[ 3^{400} , \quad 2^{600}, \quad 25^{100} , \quad 4^{200} , \quad 2^{300} \]

Según el Teorema de la Raíz Racional, los posibles ceros racionales del polinomio \[ P(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0 \] vienen dados por: \[ \dfrac{\text{factores del término constante } a_0}{\text{factores del coeficiente principal } a_n}. \]

El coeficiente principal es \( 1 \), y sus factores son: \( \pm 1 \).

El término constante es \( 6 \), y sus factores son: \( \pm 1, \pm 2, \pm 3, \pm 6 \).

Los posibles ceros racionales son: \( \pm 1, \pm 2, \pm 3, \pm 6 \).

Probando con sustitución directa:

\[ P(1) = 0, \quad P(2) = 0, \quad P(-3) = 0 \]

Como estos valores satisfacen \( P(x) = 0 \), son los ceros de \( P(x) \).

Los ceros racionales son: \( x = 1, \quad x = 2, \quad x = -3 \).

Así, el polinomio puede factorizarse como:

\[ P(x) = (x-1)(x-2)(x+3) \]

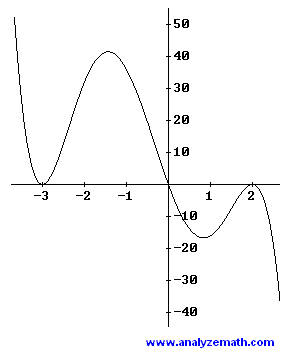
De la gráfica, \(x = -3 \) es un cero de multiplicidad \(2\), \(x = 0\) es un cero de multiplicidad 1 y \(x = 2\) es un cero de multiplicidad 2.

El polinomio tiene grado 5 y su gráfica cae a la derecha y sube a la izquierda, por lo tanto el coeficiente principal es negativo e igual a \(-1\). Así, \( P(x) \) viene dado por:

\[ P(x) = - x (x + 3)^2 (x - 2)^2 \]

Como los coeficientes de \( P(x) \) son reales, las raíces complejas deben aparecer en pares conjugados. Así, \( 2 + i \) también es un cero de \( P(x) \).

Encontramos el factor cuadrático correspondiente a estas dos raíces:

\[ (x - (2 - i))(x - (2 + i)) = (x - 2)^2 - i^2 = (x - 2)^2 + 1 = x^2 - 4x + 5. \]

Como \( P(x) \) es divisible por \( x^2 - 4x + 5 \), realizamos la división polinómica:

\[ (x^4 - 4x^3 + 3x^2 + 8x - 10) \div (x^2 - 4x + 5) = x^2 - 2. \]

Que se factoriza como:

\[ x^2 - 2 = (x - \sqrt{2})(x + \sqrt{2}). \]

Así, el conjunto completo de ceros de \( P(x) \) es:

\[ \mathbf{2 - i, \quad 2 + i, \quad -\sqrt{2}, \quad \sqrt{2}.} \]

Usamos la forma vértice de una función cuadrática:

\[ f(x) = a (x + 2)^2 + 1 \]

Sustituimos el punto \( (0, -3) \):

\[ -3 = a(0 + 2)^2 + 1 \Rightarrow -3 = 4a + 1 \Rightarrow a = -1. \]

Sustituyendo \( a = -1 \):

\[ f(x) = -(x + 2)^2 + 1 = -x^2 - 4x - 3. \]

Comparando con \( f(x) = ax^2 + bx + c \), tenemos:

\[ a = -1, \quad b = -4, \quad c = -3. \]

Como \( f(1) = 3 \) y \( f(5) = 3 \), los puntos \( (1, 3) \) y \( (5, 3) \) están en la parábola. Dado que la función es cuadrática, la coordenada \( x \) del vértice es el punto medio de estos dos puntos (ya que tienen la misma coordenada \( y \)):

\[ x_{\text{vértice}} = \dfrac{1 + 5}{2} = \dfrac{6}{2} = 3. \]

Por lo tanto, la coordenada \( x \) del vértice es \( \boxed{3} \).

La asíntota oblicua es el cociente de la división larga de \( a x^4 + b x^3 + 3 \) entre \( x^3 - 2 \).

Realizando la división:

\[ \dfrac{ax^4 + bx^3 + 3}{x^3 - 2} = ax + b + \dfrac{2ax + (3 + 2b)}{x^3 - 2} \]

El cociente \( ax + b \) debe ser igual a \( 2x - 3 \). Igualando coeficientes:

\[ a = 2, \quad b = -3. \]

Simplificamos el lado derecho:

\[ \log_2(8) = \log_2 (2^3) = 3 \]

La ecuación queda:

\[ \log_9 (x^3) = 3 \]

Reescribimos en forma exponencial:

\[ 9^3 = x^3 \Rightarrow x^3 = 9^3 \Rightarrow x = 9. \]

De \( \log_x(y^3) = 2 \), tenemos:

\[ x^2 = y^3 \]

Elevando al cuadrado ambos lados:

\[ x^4 = y^6 \]

Tomando logaritmo en base \( y \):

\[ \log_y(x^4) = \log_y(y^6) = 6. \]

Reescribiendo en forma exponencial:

\[ x^3 = 8e^3 \]

Tomando la raíz cúbica:

\[ x = \sqrt[3]{8e^3} = 2e. \]

Reescribimos:

\[ 16^x + \frac{16^x}{16} = 10 \Rightarrow 16^x \left(1 + \frac{1}{16}\right) = 10 \Rightarrow 16^x = \frac{160}{17} \]

Como \( 16^x = (2^4)^x = 2^{4x} \), tenemos:

\[ 2^{4x} = \frac{160}{17} \]

Tomando raíz cuadrada:

\[ 2^{2x} = \sqrt{\frac{160}{17}} = \frac{4\sqrt{10}}{\sqrt{17}}. \]

De \( a^2 - b^2 = 8 \), elevando al cuadrado:

\[ a^4 + b^4 - 2a^2b^2 = 64 \]

Como \( ab = 2 \), entonces \( a^2b^2 = 4 \). Sustituyendo:

\[ a^4 + b^4 - 2(4) = 64 \Rightarrow a^4 + b^4 = 72. \]

El rango de \( \sin\left( 2x - \dfrac{\pi}{3} \right) \) es \([-1, 1]\). Entonces:

\[ -2 \leq 2\sin\left( 2x - \dfrac{\pi}{3} \right) \leq 2 \] \[ -7 \leq 2\sin\left( 2x - \dfrac{\pi}{3} \right) - 5 \leq -3 \]

Tomando valor absoluto (los valores están entre -7 y -3, por lo que el valor absoluto estará entre 3 y 7):

\[ 3 \leq \left| 2\sin\left( 2x - \dfrac{\pi}{3} \right) - 5 \right| \leq 7 \]

Sumando 3:

\[ 6 \leq \left| 2\sin\left( 2x - \dfrac{\pi}{3} \right) - 5 \right| + 3 \leq 10 \]

Por lo tanto, el valor máximo es 10 y el mínimo es 6.

Para \( x < -7 \), tenemos \( x + 3 < -4 < 0 \), luego \( |3 + x| = -(3 + x) \).

Sustituyendo:

\[ |4 - (-(3 + x))| = |x + 7| \]

Como \( x + 7 < 0 \), entonces \( |x + 7| = -(x + 7) = -x - 7 \).

Sea \( d \) la distancia entre \( A \) y \( B \). El tiempo de ida es \( \frac{d}{50} \). Sea \( v \) la velocidad de retorno. El tiempo de retorno es \( \frac{d}{v} \).

La velocidad promedio total es:

\[ \frac{2d}{\frac{d}{50} + \frac{d}{v}} = 60 \]

Simplificando:

\[ \frac{2}{\frac{1}{50} + \frac{1}{v}} = 60 \Rightarrow \frac{1}{50} + \frac{1}{v} = \frac{1}{30} \Rightarrow \frac{1}{v} = \frac{1}{30} - \frac{1}{50} = \frac{2}{150} = \frac{1}{75} \]

Por lo tanto, \( v = 75 \) km/h.

Factorizando:

\[ x^2 - y^2 = (x - y)(x + y) = -12 \]

Sustituyendo \( x + y = 6 \):

\[ 6(x - y) = -12 \Rightarrow x - y = -2 \]

Resolviendo el sistema:

\[ x + y = 6, \quad x - y = -2 \Rightarrow x = 2, \quad y = 4. \]

Para \( x = 2 \):

\[ f(2) + 3f(6) = 2 \quad \text{(A)} \]

Para \( x = 6 \):

\[ f(6) + 3f(2) = 6 \quad \text{(B)} \]

Despejando \( f(6) \) de (B): \( f(6) = 6 - 3f(2) \). Sustituyendo en (A):

\[ f(2) + 3(6 - 3f(2)) = 2 \Rightarrow f(2) + 18 - 9f(2) = 2 \Rightarrow -8f(2) = -16 \Rightarrow f(2) = 2. \]

Para \( x = 0 \):

\[ f(1) = 2f(0) + 1 = 2(2) + 1 = 5 \]

Para \( x = 1 \):

\[ f(3) = 2f(1) + 1 = 2(5) + 1 = 11. \]

Sustituyendo \( y = 2x + b \) en la ecuación de la circunferencia:

\[ x^2 + (2x + b)^2 = 4 \Rightarrow 5x^2 + 4bx + b^2 - 4 = 0 \]

Para que sea tangente, el discriminante debe ser cero:

\[ \Delta = (4b)^2 - 4(5)(b^2 - 4) = 16b^2 - 20b^2 + 80 = -4b^2 + 80 = 0 \] \[ b^2 = 20 \Rightarrow b = \pm 2\sqrt{5}. \]

El divisor es \( D(x) = (x-1)(x-2) \). El resto será de la forma \( r(x) = ax + b \).

Evaluamos \( P(x) = x^{100} - x^{99} - x + 1 \) en las raíces del divisor:

\[ P(1) = 0 \Rightarrow a + b = 0 \] \[ P(2) = 2^{99}(2-1) - 2 + 1 = 2^{99} - 1 \Rightarrow 2a + b = 2^{99} - 1 \]

Resolviendo: \( a = 2^{99} - 1 \), \( b = 1 - 2^{99} \).

El resto es \( r(x) = (2^{99} - 1)x + 1 - 2^{99} \).

Sea \( y = \sqrt{\dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \sqrt{\dfrac{1}{3} + \cdots}}} \). Entonces:

\[ y^2 = \frac{1}{3} + y \Rightarrow y^2 - y - \frac{1}{3} = 0 \]

Resolviendo la cuadrática (tomando la raíz positiva):

\[ y = \frac{1 + \sqrt{1 + \frac{4}{3}}}{2} = \frac{1 + \sqrt{\frac{7}{3}}}{2} = \frac{3 + \sqrt{21}}{6}. \]

Calculamos el determinante de la matriz de coeficientes:

\[ \det(A) = \begin{vmatrix} 2 & 1 & -3 \\ -5 & 3 & 2 \\ 3 & -4 & 1 \end{vmatrix} = 2(3 \cdot 1 - 2 \cdot (-4)) - 1((-5) \cdot 1 - 2 \cdot 3) + (-3)((-5) \cdot (-4) - 3 \cdot 3) \] \[ = 2(3+8) - 1(-5-6) - 3(20-9) = 22 + 11 - 33 = 0. \]

Como el determinante es cero, el sistema no tiene solución única. Además, calculamos el determinante al reemplazar la primera columna con el vector de términos independientes:

\[ \det(A_x) = \begin{vmatrix} 5 & 1 & -3 \\ 7 & 3 & 2 \\ 8 & -4 & 1 \end{vmatrix} \neq 0 \]

Por lo tanto, el sistema es inconsistente y no tiene soluciones.