Problemas de Círculo y Trigonometría con Soluciones | Matemáticas 12º Grado
Bienvenidos a esta colección de problemas de sectores y círculos de trigonometría diseñados para estudiantes de matemáticas de 12º grado. Cada problema se enfoca en conceptos importantes como longitud de arco, ángulos centrales, coordenadas de puntos en un círculo y aplicaciones de funciones trigonométricas. Se proporcionan soluciones detalladas paso a paso para ayudar a los estudiantes a fortalecer su comprensión de la geometría del círculo y la trigonometría.
Coordenadas y Ángulos en Posición Estándar
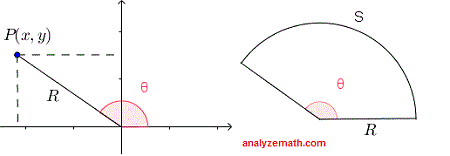
Al resolver los problemas a continuación, utilizaremos la definición de las funciones trigonométricas del ángulo \( \theta \) en términos de las coordenadas del punto \( P(x , y) \) que está en el lado terminal de un ángulo \( \theta \).
\[ \cos(\theta) = \dfrac{x}{R} \quad \tan(\theta) = \dfrac{y}{x} \quad \sec(\theta) = \dfrac{R}{x} \]
\[ \sin(\theta) = \dfrac{y}{R} \quad \cot(\theta) = \dfrac{x}{y} \quad \csc(\theta) = \dfrac{R}{y} \]
\[ R = \sqrt{x^2 + y^2} \]
También usaremos la relación entre la longitud del arco \( S \), el radio \( R \) y el ángulo central \( \theta \) de un
sector: \[ S = R \theta \quad , \quad \text{con } \theta \text{ en radianes} \]
Problema 1 - Longitud de Arco y Coordenadas en un Círculo
Dado que las coordenadas del punto \( A \), ubicado en el círculo a continuación, son \( (8, 0) \), y el arco \( s \) tiene una longitud de 20 unidades, determine las coordenadas del punto \( P \) como se muestra en el diagrama.
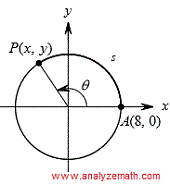
Paso 1: Usar la fórmula de longitud de arco para encontrar el ángulo \( \theta \) en radianes.
El radio \( R \) del círculo es 8. La fórmula para la longitud del arco \( s \) es:
\[ s = R \theta \]Se nos da \( s = 20 \), entonces:
\[ 20 = 8 \theta \] \[ \theta = \dfrac{20}{8} = 2.5 \text{ radianes} \]Paso 2: Usar seno y coseno para encontrar las coordenadas del punto \( P \).
\[ x = R \cos(\theta) = 8 \cos(2.5) \approx -6.40 \] \[ y = R \sin(\theta) = 8 \sin(2.5) \approx 4.79 \]Conclusión: Las coordenadas del punto \( P \) son aproximadamente:
\[ P(-6.40, \, 4.79) \]Problema 2 - Longitud de Arco Usando Tangente y Radio
En un sistema de coordenadas rectangular, un círculo con centro en el origen pasa por el punto \((4\sqrt{2},\ 5\sqrt{2})\).
¿Cuál es la longitud del arco \( S \) mostrado en la figura?

Usamos la definición de tangente para encontrar el ángulo \( \theta \).
\[ \tan(\theta) = \dfrac{y}{x} = \dfrac{5\sqrt{2}}{4\sqrt{2}} = \dfrac{5}{4} \] \[ \theta = \arctan\left(\dfrac{5}{4}\right) \]Ahora, usamos la fórmula para la longitud del arco \( s \) en términos de \( \theta \) y el radio \( R \).
\[ s = R\theta = \sqrt{(4\sqrt{2})^2 + (5\sqrt{2})^2} \cdot \arctan\left(\dfrac{5}{4}\right) \approx 8.11 \text{ unidades} \]Problema 3 - Manecilla del Minutero y Longitud de Arco
La longitud de la manecilla del minutero de un reloj es \( 4.5 \, \text{cm} \). Encuentre la longitud del arco trazado por la punta de la manecilla entre las 11:10 PM y las 11:50 PM.
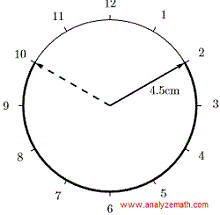
De 11:10 a 11:50, hay una diferencia de tiempo de:
\[ 40 \text{ minutos} \]Una rotación completa de la manecilla del minutero corresponde a 60 minutos y un ángulo de \( 360^{\circ} \), por lo que el desplazamiento angular por minuto es:
\[ \dfrac{360^\circ}{60} = 6^\circ \text{ por minuto} \] \[ \theta = 6^\circ \times 40 = 240^\circ \] \[ S = R \theta = 4.5 \times \left( \dfrac{240 \pi}{180} \right) = 6\pi \, \text{cm} \]Problema 4 - Geometría del Círculo con Múltiples Puntos
Los puntos \( P(a, b) \), \( Q(5, 0) \), y \( M(c, -1) \) están en un círculo centrado en \( O(0, 0) \) con radio \( R = 5 \) unidades, como se ilustra.

a) Las coordenadas \( (a,b) \) del punto \( P \).
b) La longitud del arco entre \( Q \) y \( P \) en sentido antihorario.
c) La coordenada \( c \) del punto \( M \).
d) El ángulo \( \theta \).
a)
\[ a = R \cos(35^\circ) = 5 \cos(35^\circ), \quad b = R \sin(35^\circ) = 5 \sin(35^\circ) \]b)
\[ \text{arco } PQ = R \cdot \dfrac{35 \pi}{180} = 5 \cdot \dfrac{35 \pi}{180} \approx 3.05 \, \text{ unidades} \]c)
\[ \sqrt{c^2 + (-1)^2} = 5 \quad \Rightarrow \quad c^2 + 1 = 25 \quad \Rightarrow \quad c^2 = 24 \] \[ c = \pm 2\sqrt{6} \] Dado que \( M \) está en el cuadrante III: \[ M(-2\sqrt{6}, -1) \]d)
\[ \tan(\theta + 35^\circ) = \dfrac{-1}{-2\sqrt{6}} = \dfrac{1}{2\sqrt{6}} \] \[ \theta + 35^\circ = 180^\circ + \tan^{-1}\left(\dfrac{1}{2\sqrt{6}}\right) \] \[ \theta = 180^\circ + \tan^{-1}\left(\dfrac{1}{2\sqrt{6}}\right) - 35^\circ \approx 156.54^\circ \]Problema 5 - Longitud de Arco y Distancia en un Círculo
Se muestra un círculo con radio \( R = 4 \) unidades y centro \( O \).
a) Encuentre la longitud del arco entre los puntos \( D \) y \( P \) en sentido horario.
b) Encuentre las coordenadas \( (a , b) \) del punto \( P \).
c) Encuentre la longitud del segmento \( PD \).

a)
\[ \text{Arco } DP = R \cdot \dfrac{130\pi}{180} = 4 \cdot \dfrac{130\pi}{180} \approx 9.08 \, \text{ unidades} \]b)
\[ a = 4 \cos(130^\circ), \quad b = 4 \sin(130^\circ) \]c)
\[ PD = \sqrt{(4 \cos(130^\circ) - 4)^2 + (4 \sin(130^\circ))^2} \approx 7.25 \]Problema 6 - Longitud de Arco y Coordenadas en un Círculo
En un círculo con centro \( O \) y radio \( R = 3 \), la longitud del arco \( S \) entre los puntos \( A \) y \( B \) es \[ S = 12.5 \, \text{ unidades}. \] Encuentre las coordenadas \( (a, b) \) del punto \( B \).

Problema 7 - Longitud de Arco a partir de Coordenadas
El punto \( P \) tiene coordenadas \( (4.1 , b) \) y está ubicado en el círculo, de centro \( O \) y radio \( R = 5 \), en el cuadrante I. Encuentre la longitud del arco \( S \).
