Encontrar un Polinomio Dada su Gráfica: Preguntas con Soluciones

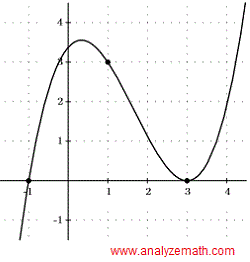
La gráfica de la función tiene un cero de multiplicidad 1 en \( x = -1 \), que corresponde al factor \( x + 1 \), y un cero de multiplicidad 2 en \( x = 3 \) (la gráfica toca pero no corta el eje x), que corresponde al factor \( (x - 3)^2 \). Por lo tanto, la función \( g \) tiene la ecuación:

\[ g(x) = k(x + 1)(x - 3)^2 \]

donde \( k \) es una constante.

La constante \( k \) se puede encontrar usando el punto con coordenadas \( (1, 3) \) que se muestra en la gráfica.

\[ g(1) = k(1 + 1)(1 - 3)^2 = 3 \]

Simplifica y resuelve para \( k \).

\[ k = \dfrac{3}{8} \]

\( g(x) \) está dada por:

\[ g(x) = \dfrac{3}{8}(x + 1)(x - 3)^2 \]

La gráfica del polinomio tiene un cero de multiplicidad 1 en \( x = 2 \) (corresponde al factor \( (x - 2) \)), otro cero de multiplicidad 1 en \( x = -2 \) (corresponde al factor \( (x + 2) \)), y un cero de multiplicidad 2 en \( x = -1 \) (la gráfica toca pero no corta el eje x, corresponde al factor \( (x + 1)^2 \)). Por lo tanto, el polinomio \( f \) tiene la ecuación:

\[ f(x) = k(x - 2)(x + 2)(x + 1)^2 \]

donde \( k \) es una constante.

La constante \( k \) se puede encontrar usando el intercepto en y \( f(0) = -1 \) que se muestra en la gráfica.

\[ f(0) = k(0 - 2)(0 + 2)(0 + 1)^2 = -1 \]

Simplifica y resuelve para \( k \).

\[ k = \dfrac{1}{4} \]

\( f(x) \) está dada por:

\[ f(x) = \dfrac{1}{4}(x - 2)(x + 2)(x + 1)^2 \]

La gráfica tiene interceptos en x en \( x = 0 \) y \( x = \dfrac{5}{2} \). Estos interceptos son los ceros del polinomio \( f(x) \). Dado que la gráfica cruza el eje x en \( x = 0 \) y \( x = \dfrac{5}{2} \), ambos ceros tienen multiplicidad impar. La gráfica en \( x = 0 \) tiene forma cúbica, por lo que el cero en \( x = 0 \) tiene multiplicidad 3. La forma de la gráfica en \( x = \dfrac{5}{2} \) es casi lineal, por lo que el cero en \( x = \dfrac{5}{2} \) tiene multiplicidad igual a 1. Usando los ceros en \( x = 0 \) y \( x = \dfrac{5}{2} \), \( f(x) \) puede escribirse como:

\[ f(x) = k(x - 0)^3 \left(x - \dfrac{5}{2}\right), \quad \text{donde } k \text{ es una constante.} \]

Ahora usamos el punto \( (2, -4) \) para encontrar \( k \).

\[ -4 = k(2)^3 \left(2 - \dfrac{5}{2}\right), \quad \text{resolviendo para } k \text{ obtenemos} \quad k = 1 \]

La ecuación del polinomio \( f(x) \) está dada por:

\[ f(x) = x^3 \left(x - \dfrac{5}{2}\right) \]

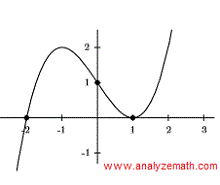
El polinomio tiene grado 3. La gráfica del polinomio tiene un cero de multiplicidad 1 en \( x = -2 \) (corresponde al factor \( x + 2 \)) y un cero de multiplicidad 2 en \( x = 1 \) (corresponde al factor \( (x - 1)^2 \)). Por lo tanto, el polinomio puede escribirse como:

\[ y = k(x + 2)(x - 1)^2 \]

Ahora necesitamos encontrar \( k \) usando el intercepto en y \( (0 , 1) \) que se muestra en la gráfica.

\[ 1 = k(0 + 2)(0 - 1)^2 = 2k \]

Resuelve para \( k \).

\[ k = \dfrac{1}{2} \]

Ahora expandimos el polinomio, lo escribimos en forma estándar e identificamos los coeficientes \( a \), \( b \), \( c \), y \( d \).

\[ y = \dfrac{1}{2}(x + 2)(x - 1)^2 = 0.5x^3 - 1.5x + 1 \]

Comparamos la expresión del polinomio encontrada arriba con:

\[ y = ax^3 + bx^2 + cx + d \]

y obtenemos los valores de los coeficientes:

\[ a = 0.5, \quad b = 0, \quad c = -1.5, \quad d = 1 \]

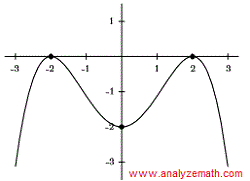
La gráfica del polinomio es simétrica con respecto al eje y, por lo tanto, la función polinómica dada debe ser una función par. Los términos \( b x^3 \) y \( d x \) incluidos en la expresión dada del polinomio no son pares, por lo que sus coeficientes son iguales a 0. Por lo tanto:

\[ b = 0 , \quad d = 0 \]

y entonces \( y \) está dada por:

\[ y = a x^4 + c x^2 + e \]

El coeficiente \( e \) se encuentra usando el intercepto en y \( (0 , -2) \) de la gráfica.

\[ -2 = a (0)^4 + c (0)^2 + e \] \[ e = -2 \]