Resuelve la desigualdad:
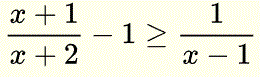
y presenta el conjunto solución usando intervalos, recta numérica y símbolos de desigualdad.
Solución en video en: desigualdad racional, pregunta 1
Resuelve la ecuación:
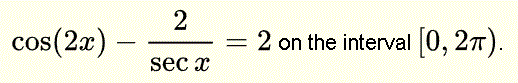
Solución en video en: ecuación trigonométrica, pregunta 2
Resuelve la ecuación:

Solución en video en: ecuación con logaritmos, pregunta 3
Resuelve la ecuación:
Solución en video en: ecuación con exponenciales, pregunta 4
Verifica la identidad:

Solución en video en: verificar identidades trigonométricas, pregunta 5
Encuentra el valor exacto de: \( \displaystyle \quad \tan \left(\dfrac{13\pi}{12}\right) \)
Solución en video en: encontrar valor exacto de función trigonométrica, pregunta 6
Cuando el polinomio \( P(x) \) se divide por \( x + 1 \), el resto es igual a \( 4 \), y cuando \( P(x) \) se divide por \( x - 2 \) da un resto igual a \( 4 \). El polinomio \( P(x) \) tiene grado \( 3 \) y tiene a \( x - 1 \) como factor. El coeficiente principal de \( P(x) \) es igual a \( 1 \). Encuentra \( P(x) \).
Solución en video en: encontrar polinomio dados restos y un factor, pregunta 7
La función \( f \) está definida por \( f(x) = - x^4 - 5x^3 - 3x^2+9x \).
a) Factoriza \( f(x) \) completamente.
b) Usa los ceros para esbozar la gráfica de \( f \).
Solución en video en: factorizar completamente y esbozar un polinomio, pregunta 8
Encuentra la ecuación de la función polinómica \( g \) cuyo grado es igual a \( 4 \) y cuya gráfica se muestra a continuación, y que toca (no corta) el eje x en \( x = -1 \).

Solución en video en: encontrar la ecuación de un polinomio dada su gráfica, pregunta 9
Para la función \( y = - 0.5 \sin \left( 4(x+\dfrac{\pi}{16}) \right) + 2.5 \), haz una tabla de valores durante 1 período y esboza la gráfica durante 2 períodos.
Solución en video en: hacer tabla de valores y esbozar gráfica, pregunta 10
La velocidad \( V \) en metros (\( m \)) de un objeto está dada por la gráfica de abajo. Escribe \( V \) como función del tiempo \( t \) en segundos (\( s \)) como una función coseno.

Solución en video en: encontrar ecuación de función trigonométrica dada por su gráfica, pregunta 11
Dada la función \[ y = \dfrac{2 x - 4}{x+2} \]
a) Encuentra el dominio de la función.
b) Encuentra las intersecciones x e y de la gráfica de la función.
c) Encuentra las ecuaciones de todas las asíntotas de la función y cualquier intersección con la gráfica de la función.
d) Haz una tabla de signos y esboza la gráfica de la función.
Solución en video en: esbozar gráfica de función racional y = (2x - 4) / (x + 2), pregunta 12
Dada la función \[ y = \dfrac{x^2-9}{x+2} \]
a) Encuentra el dominio de la función.
b) Encuentra las intersecciones x e y de la gráfica de la función.
c) Encuentra las ecuaciones de todas las asíntotas de la función.
d) Haz una tabla de signos y esboza la gráfica de la función.
Encuentra la ecuación de la función racional \( h(x) \) cuya gráfica se muestra a continuación y cuyo denominador tiene un polinomio de grado 2.

AN: (2x-4)/[(x-1)(x-2)] con discontinuidad evitable
Dada la función \( f(x) = -0.5 \log_2(x^2 - 1)-1 \).
a) Encuentra el dominio de la función.
b) Encuentra las intersecciones x e y, si las hay, de la gráfica de la función.
c) Encuentra las ecuaciones de todas las asíntotas, si las hay, de la función.
d) Haz una tabla de valores y esboza la gráfica de la función.
Dada la función \( h(x) = 2 + e^{(x-2)} \).
a) Encuentra el dominio de la función.
b) Encuentra las intersecciones x e y, si las hay, de la gráfica de la función.
c) Encuentra las ecuaciones de todas las asíntotas, si las hay, de la función.
d) Haz una tabla de valores y esboza la gráfica de la función.
Dada la función \( h(x) = \ln (2x - 1) + 2 \).
a) Encuentra el dominio y rango de la función \( h \).
b) Encuentra la inversa de la función \( h \) y especifica su dominio y rango.