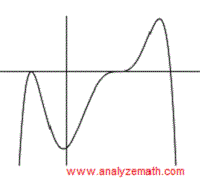
Dale cuatro razones diferentes por las cuales el gráfico a continuación no puede ser el gráfico de la función polinómica \( p(x) = x^4-x^2+1 \).
 .
.
Solución
Las cuatro razones son:
1) La función polinómica dada es par y, por lo tanto, su gráfico debe ser simétrico respecto al eje y. El gráfico dado no es simétrico respecto al eje y.
2) La función polinómica dada no tiene ceros reales (discriminante = -3: negativo). El gráfico dado tiene interceptos x que deben corresponder a ceros reales.
3) El intercepto y calculado usando p(x)( p(0) = 04 - 02 + 1 = 1) es positivo. El intercepto y del gráfico es negativo.
4) Teniendo un coeficiente principal ( = 1) positivo y un grado par ( = 4), el polinomio debe tener un gráfico que sube tanto a la derecha como a la izquierda. En el gráfico dado, ambos están cayendo.
Empareja las funciones polinómicas con sus gráficos donde se muestran todos los interceptos x.
$$f(x) = (x+1)(x-1)^2(x+2)^2$$
$$g(x) = -(x+1)(x-1)^4$$
$$h(x) = (x+1)(x-1)^3(x-3)$$
$$i(x) = (x+1)^2(x-2)^3$$
$$j(x) = (x+1)^2(1-x)(x-2)^2$$
$$k(x) =-(x+1)^2(x-1)^2(x-3)$$
 .
.
Solución
Según sus ecuaciones, todas las 6 funciones polinómicas dadas son de grado 5. Sin embargo, sus coeficientes principales son de signos diferentes. Clasificamos las 6 funciones polinómicas en 2 grupos: I y II
Grupo I - Funciones polinómicas dadas con coeficientes principales positivos
f(x) = (x + 1)(x - 1)2(x + 2)2
h(x) = (x + 1)(x - 1)3(x - 3)
i(x) = (x + 1)2(x - 2)3
Al tener grado 5 (impar) y coeficientes principales positivos, cada uno de los gráficos de las funciones anteriores (f, h e i) tiene las siguientes propiedades gráficas:
como x ____> ∞ , y ____> ∞ (el lado derecho de los gráficos sube)
como x ____> - ∞ y , ____> - ∞ (el lado izquierdo del gráfico baja)
Los gráficos dados en las partes a), c) y e) tienen las propiedades anteriores con diferentes interceptos x y sus multiplicidades. Por lo tanto,
Polinomio f(x) = (x + 1)(x - 1)2(x + 2)2 tiene un cero de multiplicidad 1 en x = -1 , un cero de multiplicidad 2 en x = 1 y un cero de multiplicidad 2 en x = - 2 y debería corresponder al gráfico en la parte e).
Polinomio h(x) = (x + 1)(x - 1)3(x - 3) tiene un cero de multiplicidad 1 en x = -1 , un cero de multiplicidad 3 en x = 1 y un cero de multiplicidad 1 en x = 3 y debería corresponder al gráfico en la parte a).
Polinomio i(x) = (x + 1)2(x - 2)3 tiene un cero de multiplicidad 2 en x = -1 y un cero de multiplicidad 3 en x = 2 y debería corresponder al gráfico en la parte c).
Grupo II - Funciones polinómicas dadas con coeficientes principales negativos
Las funciones polinómicas g, j y k, al expandirse, tienen coeficientes principales que son negativos.
g(x) = - (x + 1)(x - 1)4
j(x) = (x + 1)2(1 - x)(x - 2)2
k(x) = - (x + 1)2(x - 1)2(x - 3)
Al tener grado 5 (impar) y coeficientes principales negativos, cada uno de los gráficos de las funciones anteriores (g, j y k) tiene las siguientes propiedades gráficas:
como x ____> ∞ , y ____> - ∞ (el lado derecho de los gráficos baja)
como x ____> - ∞ y , ____> ∞ (el lado izquierdo del gráfico sube)
Los gráficos dados en las partes b), d) y f) tienen las propiedades anteriores con diferentes interceptos x y sus multiplicidades. Por lo tanto
Polinomio g(x) = - (x + 1)(x - 1)4 tiene un cero de multiplicidad 1 en x = -1 , un cero de multiplicidad 4 en x = 1 y debería corresponder al gráfico en la parte f).
Polinomio j(x) = (x + 1)2(1 - x)(x - 2)2 tiene un cero de multiplicidad 2 en x = -1 , un cero de multiplicidad 1 en x = 1 y un cero de multiplicidad 2 en x = 2 y debería corresponder al gráfico en la parte d).
Polinomio k(x) = - (x + 1)2(x - 1)2(x - 3) tiene un cero de multiplicidad 2 en x = -1 , un cero de multiplicidad 2 en x = 1 y un cero de multiplicidad 1 en x = 3 y debería corresponder al gráfico en la parte b).