Cómo usar las propiedades de las gráficas de polinomios para identificar polinomios. Se presentan preguntas de matemáticas de 12º grado con soluciones detalladas e interpretaciones gráficas.
Da cuatro razones diferentes por las cuales la gráfica a continuación no puede ser la gráfica de la función polinómica \( p(x) = x^4 - x^2 + 1 \).

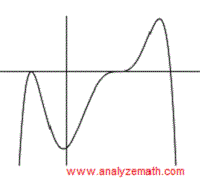
Empareja las funciones polinómicas con sus gráficas, donde se muestran todas las intersecciones con el eje x.
\[ f(x) = (x+1)(x-1)^2(x+2)^2 \]
\[ g(x) = -(x+1)(x-1)^4 \]
\[ h(x) = (x+1)(x-1)^3(x-3) \]
\[ i(x) = (x+1)^2(x-2)^3 \]
\[ j(x) = (x+1)^2(1-x)(x-2)^2 \]
\[ k(x) = -(x+1)^2(x-1)^2(x-3) \]

Según sus ecuaciones, las 6 funciones polinómicas dadas son de grado 5. Sin embargo, sus coeficientes principales tienen signos diferentes. Clasificamos los 6 polinomios en 2 grupos: I y II.
Grupo I - Polinomios dados con coeficientes principales positivos:
\[ f(x) = (x + 1)(x - 1)^2(x + 2)^2 \]
\[ h(x) = (x + 1)(x - 1)^3(x - 3) \]
\[ i(x) = (x + 1)^2(x - 2)^3 \]
Al tener grado 5 (impar) y coeficientes principales positivos, cada una de las gráficas de los polinomios anteriores \( f, h \) e \( i \) tiene las siguientes propiedades gráficas:
Cuando \( x \to \infty \), \( y \to \infty \) (el lado derecho de la gráfica sube).
Cuando \( x \to -\infty \), \( y \to -\infty \) (el lado izquierdo de la gráfica baja).
Las gráficas dadas en las partes a), c) y e) tienen las propiedades anteriores con diferentes intersecciones con el eje x y multiplicidades. Por lo tanto:
Grupo II - Polinomios dados con coeficientes principales negativos:
Las funciones polinómicas \( g \), \( j \) y \( k \), cuando se expanden, tienen coeficientes principales negativos.
\[ g(x) = - (x + 1)(x - 1)^4 \]
\[ j(x) = (x + 1)^2(1 - x)(x - 2)^2 \]
\[ k(x) = - (x + 1)^2(x - 1)^2(x - 3) \]
Al tener grado 5 (impar) y coeficientes principales negativos, cada una de las gráficas de los polinomios \( g \), \( j \) y \( k \) tiene las siguientes propiedades gráficas:
Cuando \( x \to \infty \), \( y \to -\infty \) (el lado derecho de la gráfica baja).
Cuando \( x \to -\infty \), \( y \to \infty \) (el lado izquierdo de la gráfica sube).
Las gráficas dadas en las partes \( b \), \( d \) y \( f \) exhiben las propiedades de comportamiento final anteriores, pero difieren en las intersecciones con el eje x y sus multiplicidades. Por lo tanto: