Problemas de Matemáticas de Grado 12 con Soluciones y Respuestas

Sea \(R\) y \(r\) la tasa de trabajo de las bombas grandes y pequeñas respectivamente.

\(4(2R + r) = 1\): 2 grandes y 1 pequeña trabajan 4 horas para hacer 1 trabajo

\(4(R + 3r) = 1\): 1 grande y 3 pequeñas trabajan 4 horas para hacer 1 trabajo

\(T(4R + 4r) = 1\): Encuentra el tiempo \(T\) si 4 grandes y 4 pequeñas hacen un trabajo.

Resuelve para \(R\) y \(r\) el sistema de las dos primeras ecuaciones, luego sustituye en la tercera y resuelve para \(T\) para encontrar el tiempo: \(T = \dfrac{5}{3}\) horas = 1 hora 40 minutos.

\(x + y + H = 60\): perímetro, \(x\), \(y\) y \(H\) son los dos catetos y la hipotenusa del triángulo rectángulo

\(\dfrac{1}{2}xy = 150\): área

\(x^2 + y^2 = H^2\): teorema de Pitágoras

3 ecuaciones con 3 incógnitas.

\((x + y)^2 - 2xy = H^2\): completando el cuadrado en la tercera ecuación.

\(x + y = 60 - H\): expresa \(x + y\) usando la primera ecuación y usa la segunda para encontrar \(xy = 300\) y sustituye en la ecuación 5.

\((60 - H)^2 - 600 = H^2\): una ecuación con una incógnita.

Resuelve para \(H\) para encontrar \(H = 25\) cm. Sustituye y resuelve para \(x\) y \(y\) para encontrar \(x = 15\) cm y \(y = 20\) cm.

\(\sqrt{((-6 + 2)^2 + (0 + 3)^2)} = \sqrt{((a + 3)^2 + (0 + 2)^2)}\): las distancias del centro a cualquier punto del círculo son iguales.

\(25 = (a + 3)^2 + 4\): Simplifica y eleva al cuadrado ambos lados

\((a + 3)^2 = 21\): Reescribe la ecuación anterior

Resuelve para \(a\):

\(a = -3 + \sqrt{21}\) o \(a = -3 - \sqrt{21}\)

(-2, -1): centro del círculo

\(m = \dfrac{2 - (-1)}{0 - (-2)} = \dfrac{3}{2}\): pendiente de la línea que pasa por el centro y el punto de tangencia (0, 2)

La línea que pasa por el centro y el punto de tangencia (0, 2) es perpendicular a la tangente.

\(M = -\dfrac{2}{3}\): pendiente de la tangente

\(y = -\dfrac{2}{3}x + 2\): ecuación de la tangente dada su pendiente y punto (0, 2).

\(_{3}C_{2} \times _{8}C_{6} \times 1 = 84\): Uso del teorema fundamental de conteo

\( x^2 - 3|x - 2| - 4x = - 6 \) : dada

Sea \( Y = x - 2 \) lo que da \( x = Y + 2 \)

\( (Y + 2)^2 - 3|Y| - 4(Y + 2) = - 6 \) : sustituye \( x \) por \( Y + 2 \) en la ecuación dada

\( Y^2 - 3|Y| + 2 = 0 \)

\( Y^2 = |Y|^2 \) : nota

\( |Y|^2 - 3|Y| + 2 = 0 \): reescribe la ecuación como

\( (|Y| - 2)(|Y| - 1) = 0 \): factoriza

\( |Y| = 2 , |Y| = 1 \) : resuelve para \( |Y| \)

\( Y = 2, -2 , 1 , -1 \) : resuelve para \( Y \)

\( x = 4 , 0 , 3 , 1 \) : resuelve para \( x \) usando \( x = Y + 2\)

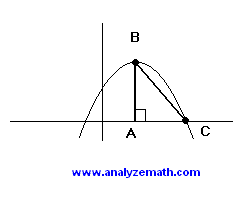
\( h = \dfrac{-b}{2a} = 2 \): coordenada x del vértice de la parábola

\( k = -(2)^2 + 4(2) + C = 4 + C \): coordenada y del vértice

\( x = \left(2 + \sqrt{4 + C} \right), \quad x = \left(2 - \sqrt{4 + C} \right) \): las dos intersecciones x de la parábola.

Longitud de \( BA = k = 4 + C \)

Longitud de \( AC = (2 + \sqrt{4 + C}) - 2 = \sqrt{4 + C} \)

\( \text{Área} = \dfrac{1}{2} BA \times AC = \dfrac{1}{2} (4 + C) \times \sqrt{4 + C} \)

\( \dfrac{1}{2} (4 + C) \times \sqrt{4 + C} = 32 \): el área es igual a 32

\( C = 12 \): resuelve lo anterior para \( C \).

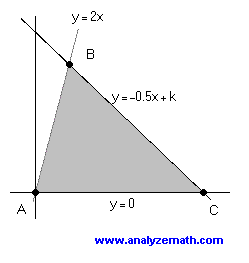
\( A(0,0) \) , \( B(2k/5 , 4k/5) \) , \( C(2k ,0) \) : puntos de intersección de las 3 líneas

Área = \( (1/2) \times (4k/5) \times (2k) = 80 \) : dado

\( k = 10 \) : resuelve la ecuación anterior para \( k \) positivo. (condición dada).

\(y = a(x + 2)(x - 3) \) : Usa las intersecciones x para escribir la ecuación de la parábola en forma factorizada

\( 10 = a(5 + 2)(5 - 2) \) ya que \( (5 , 10) \) es un punto en la gráfica de la parábola y por lo tanto satisface la ecuación.

\( a = 5/7 \) : resuelve la ecuación anterior para a.

La división de \( x^3 + 3 x^2 -2 A x + 3 \) por \( x^2 + 1 \) da el resto \( -x (1 + 2 A) \)

\( - x (1 + 2A) = 5 x \) : El resto se da como \( 5 x \)

\( -(1 + 2A) = 5 \) : los polinomios son iguales si sus coeficientes correspondientes son iguales.

\( A = -3 \) : Resuelve lo anterior para \( A \).

\( P(1) = 1^5 + 2(1^3) + A \times (1) + B = 2 \) : teorema del resto

\( P(-3) = (-3)^5 + 2(-3)^3 + A \times (-3) + B = -314 \) : teorema del resto

lo que da el sistema de ecuaciones en \( A \) y \( B \).

\[ \begin{align*} A + B = -1 \\ -3 A + B = -17 \end{align*} \]

\( A = 4 \) y \( B = -5 \) : resuelve el sistema de ecuaciones.

\( x^2 - 4x + 4 + y^2 - 4y + 4 = 4 \): expande la ecuación del primer círculo

\( x^2 - 2x + 1 + y^2 - 2y + 1 = 4 \): expande la ecuación del segundo círculo

\( -2x - 2y + 6 = 0 \): resta los términos izquierdo y derecho de las ecuaciones anteriores

\( y = 3 - x \): resuelve lo anterior para \( y \).

\( 2x^2 - 6x + 1 = 0 \): sustituye \( y \) por \( 3 - x \) en la primera ecuación, expande y agrupa términos semejantes.

\( \left(\dfrac{3}{2} + \dfrac{\sqrt{7}}{2} , \dfrac{3}{2} - \dfrac{\sqrt{7}}{2} \right), \quad \left(\dfrac{3}{2} - \dfrac{\sqrt{7}}{2} , \dfrac{3}{2} + \dfrac{\sqrt{7}}{2} \right) \): resuelve lo anterior para \(x \) y usa \( y = 3 - x \) para encontrar y.

\( I + 200 = A^2 \) : 200 añadido a \( I \) (entero desconocido) da un cuadrado.

\( I + 276 = B^2 \) : 276 añadido a \( I \) (entero desconocido) da otro cuadrado.

\( B^2 = A^2 + 76 \) : elimina \( I \) de las dos ecuaciones.

Añade cuadrados \( A^2 \) (0, 1, 4, 9, 16, 25,...) a 76 hasta obtener otro cuadrado \( B^2 \).

\( 76 + 18^2 = 400 = 20^2 \)

\( A^2 = 18^2 \quad \text{y} \quad B^2 = 20^2 \)

\( I = A^2 - 200 = 124 \)

\(sum_1 = a + a r + a r^2 = 42\): la suma de los primeros tres términos dados, \( r \) es la razón común.

\( sum_2 = (a)^2 + (a r)^2 + (a r^2)^2 = 1092\): la suma de los cuadrados de los tres términos dados.

\( sum_1 = a + ar + a r^2 = \dfrac{ a(r^3 - 1) }{r-1} = 42 \): aplica la fórmula para la suma finita de series geométricas.

\( sum_2 = a^2 + a^2 r^2 + a^2 r^4 = \dfrac{a^2 (r^6 - 1) }{(r^2 - 1) } = 1092 \): la suma de cuadrados es también una suma de series geométricas.

\( \dfrac{sum_2}{(sum_1)^2} = \dfrac{ 1092}{42^2 } = \dfrac{\dfrac{a^2{r^6 - 1}}{r^2 - 1}}{\dfrac{a^2 (r^3 - 1)^2}{(r - 1)^2}}\): define la razón.

\( \dfrac{r^2 - r + 1}{r^2 + r + 1} = \dfrac{1092}{42^2} \): simplifica la razón anterior para obtener una ecuación.

\( r = 4 , r = 1/4 \): resuelve para \( r \)

\( a = 2 \): sustituye \( r = 4 \) en \( sum_1\) y resuelve para \( a \)

\( a = 32 \): sustituye \( r = 1/4 \) en \( sum_1\) y resuelve para \( a \)

\( a = 2 , a r = 8 , a r^2 = 32 \): encuentra los tres términos para \( r = 4 \)

\( a = 32 , a r = 8 , a r^2 = 2 \): encuentra los tres términos para \( r = 1/4 \)

\( T_1 + T_2 = 3.5 : \; \) donde \( T_1 \) es el tiempo para que la roca llegue al fondo del pozo, y \( T_2 \) es el tiempo para que el sonido llegue a la parte superior.

\( 16 \times T_1^2 = 1087 \times T_2 : \; \) ya que ambos términos representan la misma distancia, que es la altura del pozo.

Resolviendo para \( T_2 \):

\( T_2 = 3.5 - T_1 \)

Sustituyendo \( T_2 \) en la ecuación:

\( 16 \times T_1^2 = 1087 \times (3.5 - T_1) \)

Resolviendo para \( T_1 \):

\( T_1 = 3.34 \text{ segundos} \)

Finalmente, calculando la altura del pozo:

\( \text{Altura} = 16 \times (3.34)^2 = 178 \text{ pies} \quad (\text{al entero más cercano}) \)

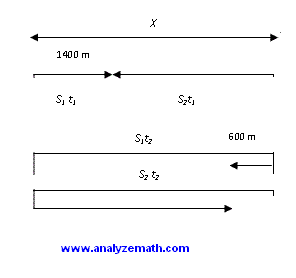
\( S_1 \times t_1 = 1400 : \; \quad S_1 \text{(es la velocidad del bote 1) } , t_1 \text{ es el tiempo para viajar 1400 metros) (bote 1)} \)

\( 1400 + S_2 \times t_1 = X : \; \quad S_2 \text{(es la velocidad del bote 2)} \)

\( S_1 \times t_2 = X + 600 \quad \text{(} t_2 \text{ es el tiempo para viajar } X + 600 \text{ metros para el bote 1)} \quad (III) \)

\( S_2 \times t_2 = 2X - 600 \quad (IV) \)

\( S_1 = \dfrac{1400}{t_1} \)

\( S_2 = \dfrac{X - 1400}{t_1} \)

\( \text{Sea} \quad T = \dfrac{t_2}{t_1} \)

Sustituyendo \( S_1 \), \( S_2 \), y \( \dfrac{t_2}{t_1} \) en las ecuaciones (III) y (IV):

\( 1400 \times T = X + 600 \)

\( X \times T - 1400 \times T = 2X - 600 \)

Resolviendo el sistema de dos ecuaciones con dos incógnitas \( X \) y \( T \) eliminando \( T \) y resolviendo para \( X \) para obtener el ancho \( X \) del río:

\( X = 3600 \text{ metros} \)

Resuelve el sistema de las dos primeras ecuaciones para obtener la solución \( (2, -3) \).

La solución \( (2, -3) \) también debe ser la solución de las dos últimas ecuaciones ya que las 4 líneas pasan por el mismo punto \( (2, -3) \).

\( a(2) + b(-3) = 4 : \;\) sustituye x por 2 e y por -3 en la tercera ecuación

\( 2a(2) - b(-3) = 2 : \; \) sustituye x por 2 e y por -3 en la cuarta ecuación

Resolviendo para \( a \) y \( b \) el sistema de ecuaciones anterior para obtener:

\( a = 1, \quad b = -\dfrac{2}{3} \)

Trabajemos con ecuaciones de líneas.

La pendiente de \( AB \) es igual a \( -3 \) ya que es perpendicular a \( OB \), cuya pendiente es \( \dfrac{1}{3} \).

La ecuación de \( AB \) está dada por: \( y = -3x + B \)

Como \( AB \) pasa por el punto \( C(5,5) \), tenemos \( 5 = -3 \times 5 + B \), resolvemos para B para encontrar la ecuación de \( AB \): \( y = -3x + 20 \)

Las coordenadas del punto \( B \) se encuentran resolviendo el sistema: \( y = -3x + 20 \) y \( y = \dfrac{1}{3}x \).

Resolviendo para \( (x,y) \), obtenemos \( B(6,2) \).

De manera similar, las coordenadas del punto \( A \) se encuentran resolviendo el sistema: \( y = -3x + 20 \) y \( y = 2x \).

Resolviendo para \( (x,y) \), obtenemos \( A(4,8) \).

Calculamos la distancia \( \overline{OB} \): \( \overline{OB} = \sqrt{6^2 + 2^2} = \sqrt{40} \)

Y la distancia \( \overline{AB} \): \( \overline{AB} = \sqrt{(6-4)^2 + (2-8)^2} = \sqrt{40} \)

El área del triángulo \( OAB \) es: \( \text{Área} = \dfrac{1}{2} \times \overline{OB} \times \overline{AB} = \dfrac{1}{2} \times 40 = 20 \)

Sea \( t \) el tiempo (en horas) que le toma a la bomba B vaciar la piscina sola.

La bomba A tarda \( t - 2 \) horas en vaciar la piscina sola.

La bomba A trabaja durante 4 horas (de 8:00 a.m. a 12:00 p.m.) a la tasa \( \dfrac{1}{t - 2} \).

La bomba B trabaja durante 2 horas (de 10:00 a.m. a 12:00 p.m.) a la tasa \( \dfrac{1}{t} \).

El trabajo total realizado por ambas bombas a las 12:00 p.m. es 60% de la piscina: \( \dfrac{4}{t - 2} + \dfrac{2}{t} = 0.6 \).

Multiplica todos los términos de la ecuación anterior por \( t(t - 2) \) y simplifica: \( 4t + 2(t - 2) = 0.6t(t - 2) \).

La ecuación anterior se puede escribir como: \( 0.6t^2 - 7.2t + 4 = 0 \).

Usando la fórmula cuadrática, encontramos: \( t = \dfrac{36 \pm 4\sqrt{66}}{6} = 6 \pm \dfrac{2\sqrt{66}}{3} \).

La solución válida es \( t = 6 + \dfrac{2\sqrt{66}}{3} \).

El tiempo de la bomba A para vaciar la piscina sola es \( t - 2 = 4 + \dfrac{2\sqrt{66}}{3} \).

La tasa de la bomba A es \( r = \dfrac{1}{4 + \dfrac{2\sqrt{66}}{3}} \).

Tiempo requerido para vaciar el 40% de la piscina: \( \text{Tiempo} = \dfrac{0.4}{r} = 0.4 \times \left(4 + \dfrac{2\sqrt{66}}{3}\right) \).

El tiempo después de las 12:00 p.m. que le toma a la bomba A vaciar la piscina es: \( \boxed{ 0.4 \times \left(4 + \dfrac{2\sqrt{66}}{3}\right) \approx 3.766 \; \text{horas}} \).

Sea \( x \) el número de alumnos (niños y niñas) en la escuela A.

Sea \( y \) el número de alumnos (niños y niñas) en la escuela B.

Nos dan que el número de alumnos en la escuela A es la mitad que en la escuela B: \( x = \dfrac{y}{2} \).

Sea \( b_A \) y \( b_B \) el número de niños en las escuelas A y B, respectivamente. La proporción de niños en la escuela A a la escuela B es: \( b_A : b_B = 1 : 3 \). Esto significa: \( b_B = 3 b_A \).

También nos dan que el número de niños en la escuela B es 200 más que en la escuela A: \( b_B = b_A + 200 \).

Usando \( b_B = 3b_A \), sustituimos: \( 3b_A = b_A + 200 \).

Resolviendo para \( b_A \): \( 2b_A = 200 \), \( b_A = 100 \). Así, \( b_B = 300 \).

Sea \( g_A \) y \( g_B \) el número de niñas en las escuelas A y B, respectivamente. La proporción de niñas en la escuela A a la escuela B es: \( g_A : g_B = 3 : 5 \). Esto significa: \( g_B = \dfrac{5}{3} g_A \).

Sabemos: \( x = b_A + g_A \) y \( y = b_B + g_B \).

Sustituyendo \( x = \dfrac{y}{2} \): \( b_A + g_A = \dfrac{b_B + g_B}{2} \).

Sustituyendo valores conocidos: \( 100 + g_A = \dfrac{300 + g_B}{2} \).

Usando \( g_B = \dfrac{5}{3} g_A \): \( 100 + g_A = \dfrac{300 + \dfrac{5}{3} g_A}{2} \).

Multiplicando ambos lados por 2: \( 200 + 2g_A = 300 + \dfrac{5}{3} g_A \).

Multiplicando todos los términos por 3: \( 600 + 6g_A = 900 + 5g_A \), \( g_A = 300 \).

Entonces, \( g_B = 500 \).

Respuesta final: En la escuela A hay 100 niños, 300 niñas y un total de 400 alumnos. En la escuela B hay 300 niños, 500 niñas y un total de 800 alumnos.

Sea \( L \) la tasa de una bomba grande (piscina por hora).

Sea \( S \) la tasa de una bomba pequeña (piscina por hora).

Cuatro bombas grandes y dos pequeñas llenan la piscina en 2 horas, por lo tanto: \( 2(4L + 2S) = 1 \).

Dos bombas grandes y seis pequeñas llenan la piscina en 2 horas, por lo tanto: \( 2(2L + 6S) = 1 \).

Reescribe el sistema de dos ecuaciones para \( L \) y \( S \) como: \( 8L + 4 S = 1 \) y \( 4L + 12 S = 1 \).

Multiplica la segunda ecuación por 2: \( 8L + 24S = 2 \).

Resta la primera ecuación de la anterior: \( -20 S = -1 \), \( S = \dfrac{1}{20} \).

Sustituye \( S = \dfrac{1}{20} \) en la ecuación \( 8L + 4 S = 1 \): \( 8L + 4 (\dfrac{1}{20}) = 1 \).

Resuelve la ecuación anterior para \( L \): \( L = \dfrac{1}{10} \).

Encuentra la tasa de 8 bombas grandes y 8 pequeñas: \( \text{Tasa total} = 8L + 8S = \dfrac{8}{10} + \dfrac{8}{20} = \dfrac{6}{5} \).

Como las bombas juntas llenan \( \dfrac{6}{5} \) de la piscina por hora, el tiempo requerido para llenar \( 50\%\) de la piscina es: \( {\dfrac{6}{5}} t = 50\% \), entonces \( t = \dfrac{5}{12} \text{ horas} = 25 \text{ minutos} \).

Tomará 25 minutos llenar \( 50\% \) de la piscina con 8 bombas grandes y 8 pequeñas.