Aplicaciones Reales de las Funciones Sinusoidales con Soluciones
Problemas con Soluciones
Las funciones seno son herramientas matemáticas poderosas utilizadas para modelar fenómenos periódicos que se repiten en el tiempo. Esta página web explora cómo las funciones seno ayudan a resolver problemas del mundo real que involucran movimiento, ciclos y oscilaciones. Ya sea analizando el movimiento de una masa oscilante, prediciendo el número de horas de luz diurna a lo largo del año, estimando temperaturas medias mensuales, modelando la rotación de una rueda de la fortuna, comprendiendo las mareas altas y bajas, u optimizando el rendimiento de paneles solares, las funciones sinusoidales proporcionan soluciones precisas y prácticas. Profundice en cada ejemplo para ver cómo las matemáticas se encuentran con el mundo real a través de modelos sinusoidales.
Problema 1
Una masa unida a un resorte se tira hacia el suelo de modo que su altura sobre el piso es de 10 mm (milímetros). Luego se suelta la masa y comienza a moverse hacia arriba y hacia abajo, alcanzando alturas máximas y mínimas de 20 y 10 mm, respectivamente, con un ciclo de 0.8 segundos.
- Suponga que la altura \( h(t) \) de la masa es una función sinusoidal, donde \( t \) es el tiempo en segundos. Dibuje una gráfica de \( h \) desde \( t = 0 \) hasta \( t = 0.8 \) segundos. \( t = 0 \) es el momento en que se suelta la masa.
- Encuentre una función sinusoidal para la altura \( h(t) \).
- ¿Durante cuántos segundos la altura de la masa está por encima de 17 mm en un ciclo?
Solución
-
La masa se suelta en \( t = 0 \) cuando \( h \) es mínima. Medio ciclo después, \( h \) alcanza su máximo y otro medio ciclo después vuelve a alcanzar su mínimo. Por lo tanto, en un ciclo, \( h \) varía con \( t \) de la siguiente manera:
-
Según la gráfica obtenida en la parte a), \( h(t) \) podría modelarse mediante una función coseno desplazada verticalmente hacia arriba y horizontalmente hacia la derecha. Por lo tanto:
\[
h(t) = a \cos[ b(t - d) ] + c
\]
Sea \( h_{\text{max}} \) el valor máximo de \( h \) y \( h_{\text{min}} \) el valor mínimo de \( h \). Por lo tanto:
\[
|a| = \frac{h_{\text{max}} - h_{\text{min}}}{2} = \frac{20 - 10}{2} = 5 , \quad a = \pm 5
\]
\[
c = \frac{h_{\text{max}} + h_{\text{min}}}{2} = \frac{20 + 10}{2} = 15
\]
\[
\text{Período} = \frac{2\pi}{|b|} = 0.8 \Rightarrow b = \pm 2.5\pi
\]
Usamos \( a = 5 \) y \( b = 2.5\pi \). El desplazamiento de la función coseno es hacia la derecha e igual a medio período. Por lo tanto, \( d = 0.4 \):
\[
h(t) = 5 \cos[ 2.5\pi(t - 0.4) ] + 15
\]
Comprobamos que \( h \) tiene un mínimo en \( t = 0 \):
\[
h(0) = 5 \cos[ 2.5\pi(0 - 0.4) ] + 15 = 5 \cos( -\pi ) + 15 = 10
\]
Comprobamos que \( h \) tiene un máximo en \( t = 0.4 \):
\[
h(0.4) = 5 \cos[ 2.5\pi(0.4 - 0.4) ] + 15 = 5 \cos( 0 ) + 15 = 20
\]
-
A continuación se muestra la gráfica de \( y = h(t) \) y \( y = 17 \). Primero necesitamos encontrar \( t_1 \) y \( t_2 \), que son los valores de \( t \) para los cuales \( h(t) = 17 \), resolviendo la ecuación:
\[
5 \cos[ 2.5\pi(t - 0.4) ] + 15 = 17
\]
\[
\cos[ 2.5\pi(t - 0.4) ] = \frac{17 - 15}{5} = 0.4
\]
\[
2.5\pi(t - 0.4) = \arccos(0.4)
\]
\[
t = \frac{\arccos(0.4)}{2.5\pi} + 0.4 = 0.547 \text{ segundos}
\]
La solución \( t \) encontrada anteriormente es mayor que \( 0.4 \), que es la posición del máximo, y menor que \( 0.8 \), por lo tanto corresponde a \( t_2 \). Así que:
\[
t_2 = \frac{\arccos(0.4)}{2.5\pi} + 0.4 = 0.547 \text{ segundos}
\]
\( t_1 \) se obtiene usando la simetría de las dos soluciones con respecto a la posición del máximo en \( t = 0.4 \). Por lo tanto:
\[
t_1 = 0.4 - (0.547 - 0.4) = 0.252 \text{ segundos}
\]
La altura de la masa es mayor que 17 metros durante:
\[
t_2 - t_1 = 0.547 - 0.252 = 0.295 \text{ segundos}
\]
Problema 2
El número de horas de luz diurna \( H \) en cierta área está dado aproximadamente por la función:
\[
H(t) = 2.5 \cos\left[ b(t - d) \right] + 11.5
\]
donde \( H \) está en horas y \( t \) en días, y la función tiene un período de un año (365 días).
- Encuentre \( b \) (\( b > 0 \)) y \( d \) si \( H \) es máxima el 21 de junio (el mes de febrero tiene 28 días).
- ¿Qué día es el más corto (tiene el menor número de horas de luz diurna)?
Solución
-
Dado que el período es conocido e igual a 365 días, usamos la fórmula:
\[
365 = \frac{2\pi}{b} \quad \Rightarrow \quad b = \frac{2\pi}{365}
\]
Si establecemos \( d = 0 \) en la función:
\[
H(t) = 2.5 \cos[b(t - d)] + 11.5
\]
se convierte en:
\[
H(t) = 2.5 \cos(bt) + 11.5
\]
que tiene un máximo en \( t = 0 \).
En nuestro problema, el máximo ocurre el 21 de junio, que corresponde a:
\[
t = 31 + 28 + 31 + 30 + 31 + 21 = 172
\]
(días desde el 1 de enero hasta el 21 de junio).
Por lo tanto, el desplazamiento horizontal es 172 unidades hacia la derecha, y \( d = 172 \). Así que:
\[
H(t) = 2.5 \cos\left[\frac{2\pi}{365}(t - 172)\right] + 11.5
\]
-
El día más corto corresponde al valor de \( t \) que da el mínimo de \( H \), que es:
\[
11.5 - 2.5 = 9
\]
Resolvemos la ecuación:
\[
2.5 \cos\left[\frac{2\pi}{365}(t - 172)\right] + 11.5 = 9
\]
\[
\cos\left[\frac{2\pi}{365}(t - 172)\right] = \frac{9 - 11.5}{2.5} = -1 = \cos(\pi)
\]
lo que da:
\[
\frac{2\pi}{365}(t - 172) = \pi
\]
\[
t = \frac{365\pi}{2\pi} + 172 = 354.5 \text{ días}
\]
Nota: También podríamos determinar esto reconociendo que el tiempo desde un máximo hasta el mínimo siguiente en una función coseno es la mitad del período. Por lo tanto, el mínimo ocurre en:
\[
t = 172 + \frac{1}{2}(365) = 354.5 \text{ días}
\]
Para calcular el número de días desde enero hasta noviembre:
\[
t = 31 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 31 + 30 = 334
\]
Luego, el número de días en diciembre es:
\[
354.5 - 334 = 20.5
\]
que corresponde aproximadamente al 21 de diciembre.
Problema 3
La temperatura promedio mensual \( T \) (en \( ^{\circ} \mathrm{C} \)) en cierta ciudad puede aproximarse por:
\[
T(t) = a \cos\left[ b(t - d) \right] + c
\]
donde \( t \) es el tiempo en meses, \( t = 0 \) corresponde al 1 de enero, y asumimos que la función \( T(t) \) tiene un período de 12 meses.
- Encuentre \( a \), \( b \) (con \( b > 0 \)), \( c \), y \( d \) si \( T \) tiene un máximo de \( 22.4^{\circ} \mathrm{C} \) a mediados de julio (\( t = 6.5 \)) y un mínimo de \( -10^{\circ} \mathrm{C} \).
- ¿En qué mes es \( T \) mínima?
- ¿Durante cuántos meses es \( T \) mayor que \( 18^{\circ} \mathrm{C} \)?
Solución
-
Los valores mínimo y máximo de \( T \), denotados \( T_{\text{max}} \) y \( T_{\text{min}} \) respectivamente, nos permiten encontrar \( a \) y \( c \) de la siguiente manera:
Se nos da:
\[
T_{\text{max}} = 22.4 \quad \text{y} \quad T_{\text{min}} = -10
\]
\[
c = \frac{T_{\text{max}} + T_{\text{min}}}{2} = 6.2
\]
\[
|a| = \frac{T_{\text{max}} - T_{\text{min}}}{2} = 16.2 \quad \text{(tomamos } a > 0 \text{)}
\]
La gráfica de \( T \) es la de una función coseno \( a \cos(bt) \) desplazada 6.5 unidades a la derecha. Por lo tanto:
\[
T(t) = 16.2 \cos[ b(t - 6.5) ] + 6.2
\]
Ahora usamos el período para encontrar \( b \). El período es 12, y dado que:
\[
\text{Período} = \frac{2\pi}{b} = 12 , \quad \text{obtenemos } b = \frac{\pi}{6}
\]
Así, la función de temperatura es:
\[
T(t) = 16.2 \cos\left[ \frac{\pi}{6}(t - 6.5) \right] + 6.2
\]
-
Encuentre \( t \) para el cual \( T \) es mínima. El valor mínimo de \( T \) es -10. Resolvemos:
\[
16.2 \cos\left[ \frac{\pi}{6}(t - 6.5) \right] + 6.2 = -10
\]
\[
\cos\left[ \frac{\pi}{6}(t - 6.5) \right] = -1 = \cos(\pi)
\]
\[
\frac{\pi}{6}(t - 6.5) = \pi
\]
\[
t = 12.5
\]
Nota: Podríamos haber respondido esto usando el hecho de que la distancia entre un máximo y el mínimo siguiente en una función sinusoidal es la mitad del período. Así que:
\[
t = 6.5 + \frac{1}{2}(12) = 12.5 \text{ días}
\]
Dado que \( t = 12.5 \) es un poco más de un período (12 meses), corresponde a mediados de enero, lo que significa que la temperatura es mínima alrededor de ese tiempo.
-
Ahora encontramos los tiempos \( t_1 \) y \( t_2 \) en los que \( T = 18 \) resolviendo la ecuación:
\[
16.2 \cos\left[ \frac{\pi}{6}(t - 6.5) \right] + 6.2 = 18
\]
\[
\cos\left[ \frac{\pi}{6}(t - 6.5) \right] = \frac{18 - 6.2}{16.2}
\]
\[
\frac{\pi}{6}(t - 6.5) = \arccos\left( \frac{18 - 6.2}{16.2} \right)
\]
\[
t = \frac{6}{\pi} \arccos\left( \frac{18 - 6.2}{16.2} \right) + 6.5 = 7.94 \text{ meses}
\]
De la gráfica de \( T(t) \) y la línea horizontal \( y = 18 \), la solución \( t = 7.94 \) corresponde a \( t_2 = 7.94 \). Por simetría:
\[
t_1 = 6.5 - (t_2 - 6.5) = 6.5 - (7.94 - 6.5) = 5.06 \text{ meses}
\]
El número de meses durante los cuales \( T > 18 \) es:
\[
t_2 - t_1 = 7.94 - 5.06 = 2.88 \text{ meses (aproximadamente 3 meses)}
\]
Problema 4
El diámetro de una gran rueda de la fortuna es de 48 metros y toma 2.8 minutos para que la rueda complete una revolución. Un pasajero sube a la rueda en su punto más bajo, que está a 60 cm del suelo, en \( t = 0 \).
- Encuentre una función sinusoidal \( h(t) \) que dé la altura \( h \), en metros, del pasajero sobre el suelo como función del tiempo \( t \) en minutos.
- Encuentre los intervalos de tiempo durante los cuales la altura del pasajero es menor a 30 metros, desde \( t = 0 \) hasta \( t = 2.8 \) minutos.
- ¿Cuántos minutos, desde \( t = 0 \), tarda el pasajero en alcanzar el punto más alto por segunda vez?
Solución
-
La altura mínima \( h_{\text{min}} \) sobre el suelo es 0.6 metros. La altura máxima \( h_{\text{max}} \) es igual a la altura mínima más el diámetro de la rueda.
\[
h_{\text{max}} = 0.6 + 48 = 48.6
\]
Dado que \( h(t) \) es mínima en \( t = 0 \), sería más fácil modelarla mediante una función coseno reflejada. Por lo tanto:
\[
h(t) = a \cos[b(t - d)] + c
\]
\[
|a| = \frac{h_{\text{max}} - h_{\text{min}}}{2} = -\frac{48.6 - 0.6}{2} = 24
\]
Dos soluciones para \( a \) son \( \pm 24 \). Seleccionamos \( a = -24 \), donde el signo menos representa la reflexión en el eje horizontal.
\[
c = \frac{h_{\text{max}} + h_{\text{min}}}{2} = \frac{48.6 + 0.6}{2} = 24.6
\]
El período es 2.8, y dado que:
\[
\text{período} = \frac{2\pi}{b} \Rightarrow b = \frac{2\pi}{2.8}
\]
\[
h(t) = -24 \cos\left( \frac{2\pi}{2.8} t \right) + 24.6
\]
Comprobación:
En \( t = 0 \),
\[
h(0) = -24 \cos(0) + 24.6 = -24(1) + 24.6 = 0.6 \, \text{m}
\]
En \( t = 1.4 \) (medio período después),
\[
h(1.4) = -24 \cos\left( \frac{2\pi}{2.8} \cdot 1.4 \right) + 24.6 = -24 \cos(\pi) + 24.6 = 48.6 \, \text{m}
\]
-
Primero necesitamos resolver la ecuación:
\[
-24 \cos\left( \frac{2\pi}{2.8} t \right) + 24.6 = 30
\]
\[
\cos\left( \frac{2\pi}{2.8} t \right) = \frac{30 - 24.6}{-24}
\]
\[
t = \frac{2.8}{2\pi} \arccos\left( \frac{30 - 24.6}{-24} \right) = 0.8 \, \text{minutos}
\]
La solución corresponde a \( t_1 \), la primera intersección de la gráfica de \( h(t) \) y la línea \( y = 30 \). Por lo tanto:
\[
t_1 = 0.8 \, \text{min}, \quad t_2 = 2.8 - 0.8 = 2 \, \text{min}
\]
\( h(t) \lt 30 \) desde \( t = 0 \) hasta \( t = 0.8 \) y desde \( t = 2 \) hasta \( t = 2.8 \), para un total de 1.6 minutos.
-
El pasajero alcanza el máximo en \( t = \frac{1}{2} \cdot 2.8 \) por primera vez y nuevamente en:
\[
t = \frac{1}{2} \cdot 2.8 + 2.8 = 4.2 \, \text{minutos}
\]
para alcanzar la altura máxima por segunda vez.
Problema 5
Debido a las atracciones gravitacionales de la luna y el sol sobre la Tierra, el agua en mares y océanos tiende a subir y bajar periódicamente, lo que se conoce como mareas altas y bajas. En una situación típica, el tiempo entre dos mareas altas es cercano a 12 horas. En cierta área costera, la profundidad del agua puede aproximarse mediante una función sinusoidal de la forma:
\[
d(t) = -2.5 \cos[ b(t - 2) ] + 3.5
\]
donde \( d \) está en metros y \( t \) en horas, con \( t = 0 \) correspondiendo a las 12 am.
- Encuentre \( b \) (\( b > 0 \)) si \( d \) tiene un período de 12 horas.
- Desde \( t = 0 \) hasta \( t = 12 \), ¿a qué hora es \( d \) mínima (marea baja) y a qué hora es máxima (marea alta)?
- Desde \( t = 0 \) hasta \( t = 12 \), ¿cuáles son los intervalos de tiempo durante los cuales la profundidad del agua es de 4.5 metros o más?
Solución
-
Usando el período, tenemos:
\[
12 = \frac{2\pi}{b}
\]
\[
b = \frac{\pi}{6}
\]
-
\( d(t) \) ahora está dada por:
\[
d(t) = -2.5 \cos\left( \frac{\pi}{6}(t - 2) \right) + 3.5
\]
El valor más pequeño de \( d \) es:
\[
-2.5 + 3.5 = 1
\]
Por lo tanto, \( d \) es mínima para \( t \) tal que:
\[
-2.5 \cos\left( \frac{\pi}{6}(t - 2) \right) + 3.5 = 1
\]
Resolvemos para obtener:
\[
\cos\left( \frac{\pi}{6}(t - 2) \right) = 1
\]
\[
\frac{\pi}{6}(t - 2) = 0
\]
\[
t = 2 \quad \text{(correspondiente a las 2 am)}
\]
El valor más alto de \( d \) es:
\[
2.5 + 3.5 = 6
\]
Por lo tanto, \( d \) es máxima para \( t \) tal que:
\[
-2.5 \cos\left( \frac{\pi}{6}(t - 2) \right) + 3.5 = 6
\]
Resolvemos para obtener:
\[
\cos\left( \frac{\pi}{6}(t - 2) \right) = -1
\]
\[
\frac{\pi}{6}(t - 2) = \pi
\]
\[
t = 8 \quad \text{(correspondiente a las 10 am)}
\]
NOTA: Podríamos haber respondido la parte b) usando el hecho de que la distancia entre un mínimo y el máximo siguiente en una función sinusoidal es la mitad del período. Por lo tanto:
\[
d \text{ es máxima en } t = 2 + \frac{1}{2} \cdot 12 = 8
\]
-
Primero necesitamos encontrar \( t \) para el cual \( h(t) = 4.5 \) resolviendo la ecuación:
\[
-2.5 \cos\left( \frac{\pi}{6}(t - 2) \right) + 3.5 = 4.5
\]
que puede escribirse como:
\[
\cos\left( \frac{\pi}{6}(t - 2) \right) = \dfrac{1}{-2.5}
\]
Resolvemos para \( t \):
\[
t_1 = \dfrac{6}{\pi}\cdot \arccos\left( -\frac{1}{2.5} \right) + 2 = 5.8 \text{ horas}
\]
\[
t_2 = 8 + (8 - 5.8) = 10.2 \text{ horas (usando simetría con respecto a la posición del máximo)}
\]
El número total de horas durante las cuales \( d(t) > 4.5 \, \text{m} \) es:
\[
10.2 - 5.8 = 4.4 \text{ horas}
\]
Problema 6
Debido a las mareas altas y bajas, la profundidad \( d \) del agua en cierta área costera puede expresarse mediante una función sinusoidal. La marea más alta ocurre a las 8 am y la marea más baja ocurre 6 horas después. El nivel máximo de agua es de 2.8 metros y el nivel más bajo de agua es de 0.4 metros.
- Use funciones sinusoidales para encontrar la profundidad \( d(t) \) del agua, en metros, como función del tiempo \( t \) en horas. (Suponga que las 8 am corresponden a \( t = 0 \)).
- Encuentre la profundidad del agua al mediodía.
- Use la gráfica de \( d(t) \) y cálculos analíticos para calcular el intervalo de tiempo durante el cual la profundidad \( d \) está por debajo de \( 1.5 \, \text{m} \) desde las 12 pm hasta las 6 pm.
Solución
-
Sea \( d(t) \) escrita como:
\[
d(t) = a \cos[b(t - d)] + c
\]
El mínimo \( d_{\min} \) y el máximo \( d_{\max} \) de \( d \) son:
\[
d_{\min} = 0.4
\]
\[
d_{\max} = 2.8
\]
\[
c = \frac{d_{\max} + d_{\min}}{2} = \frac{2.8 + 0.4}{2} = 1.6
\]
\[
|a| = \frac{d_{\max} - d_{\min}}{2} = \frac{2.8 - 0.4}{2} = 1.2
\]
Dado que \( d(t) \) tiene un mínimo en \( t = 0 \) (8 am), podemos seleccionar \( a = -1.2 \) y \( d = 0 \):
\[
d(t) = -1.2 \cos(bt) + 1.6
\]
donde es fácil verificar que \( d = -1.2 + 1.6 = 0.4 \) en \( t = 0 \).
Ahora usamos el período para encontrar \( b \) (\( b > 0 \)) de la siguiente manera:
\[
\text{período} = 12 = \frac{2\pi}{b}
\]
\[
\Rightarrow b = \frac{\pi}{6}
\]
\( d(t) \) ahora se escribe como:
\[
d(t) = -1.2 \cos\left( \frac{\pi}{6}t \right) + 1.6
\]
donde es fácil verificar que el máximo ocurre en \( t = 6 \).
-
Al mediodía \( t = 4 \), por lo tanto:
\[
d(4) = -1.2 \cos\left( \frac{\pi}{6} \cdot 4 \right) + 1.6 = 2.2 \, \text{m}
\]
-
La gráfica de \( d(t) \) se muestra a continuación con líneas verticales correspondientes a las 12 pm hasta las 6 pm y una línea horizontal correspondiente a \( d = 1.5 \). La profundidad del agua es menor que 1.5 desde \( t_0 \) hasta las 6 pm (\( t = 10 \)). Necesitamos encontrar \( t_0 \), que es un punto de intersección de \( d(t) \) y \( y = 1.5 \), resolviendo la ecuación:
\[
-1.2 \cos\left( \frac{\pi}{6}t \right) + 1.6 = 1.5
\]
\[
t = \frac{6 \cdot \arccos\left( \frac{1.5 - 1.6}{-1.2} \right)}{\pi} \approx 2.84
\]
La solución encontrada corresponde al punto de intersección izquierdo de \( d(t) \) y \( y = 1.5 \). El punto derecho \( t_0 \) puede encontrarse usando la simetría de la gráfica con respecto al punto máximo. Por lo tanto:
\[
t_0 = 6 + (6 - 2.84) = 9.16 \, \text{horas}
\]
0.16 horas corresponde a:
\[
0.16 \times 60 \, \text{minutos} \approx 10 \text{ minutos}
\]
9.16 horas corresponde aproximadamente a:
\[
\approx 5:10 \, \text{pm}
\]
Desde las 12 pm hasta las 6 pm, la profundidad del agua está por debajo de 1.5 desde las 5:10 pm hasta las 6 pm.
Problema 7
Un sistema de paneles solares produce una potencia promedio diaria \( P \) que cambia durante el año. Es máxima el 21 de junio (día con el mayor número de horas de luz diurna) e igual a \( 20 \ \text{kWh/día} \). Suponemos que \( P \) varía con el tiempo \( t \) según la función sinusoidal:
\[
P(t) = a \cos[b(t - d)] + c
\]
donde \( t = 0 \) corresponde al 1 de enero, \( P \) es la potencia en kWh/día, y \( P(t) \) tiene un período de 365 días (28 días en febrero). El valor mínimo de \( P \) es \( 4 \ \text{kWh/día} \).
- Encuentre los parámetros \( a \), \( b \), \( c \), y \( d \).
- Dibuje \( P(t) \) en un período desde \( t = 0 \) hasta \( t = 365 \).
- ¿Cuándo es mínima la potencia producida por el sistema solar?
- La potencia producida por este sistema solar es suficiente para alimentar un grupo de máquinas si la potencia producida por el sistema es mayor o igual a \( 16 \ \text{kWh/día} \). ¿Durante cuántos días, en un año, es suficiente la potencia producida por el sistema?
Solución
-
Sea \( P(t) \) escrita como:
\[
P(t) = a \cos[b(t - d)] + c
\]
El mínimo \( P_{\text{min}} \) y el máximo \( P_{\text{max}} \) de \( P(t) \) están dados:
\[
P_{\text{min}} = 4
\]
\[
P_{\text{max}} = 20
\]
\[
c = \frac{P_{\text{max}} + P_{\text{min}}}{2} = \frac{20 + 4}{2} = 12
\]
\[
|a| = \frac{P_{\text{max}} - P_{\text{min}}}{2} = \frac{20 - 4}{2} = 8
\]
Ahora necesitamos encontrar el número de días \( t \) después del 1 de enero en el que \( P(t) \) es máxima contando los días de los meses desde enero hasta mayo y sumando 21 días en junio:
\[
t = 31 + 28 + 31 + 30 + 31 + 21 = 172
\]
Ahora usamos el período para encontrar \( b \) (con \( b > 0 \)) de la siguiente manera:
\[
\text{período} = 365 = \frac{2\pi}{b}
\]
\[
\Rightarrow b = \frac{2\pi}{365}
\]
Una función coseno sin desplazamiento tiene un máximo en \( t = 0 \). \( P(t) \) tiene un máximo en \( t = 172 \). Podemos modelar \( P(t) \) mediante una función coseno desplazada 172 unidades a la derecha:
\[
P(t) = 8 \cos\left(\frac{2\pi}{365}(t - 172)\right) + 12
\]
Comprobamos que \( P(t) \) es máxima en \( t = 172 \):
\[
P(172) = 8 \cos\left(\frac{2\pi}{365}(172 - 172)\right) + 12 = 8 \cos(0) + 12 = 20
\]
-
La gráfica de \( P(t) \) se muestra a continuación.
(Ver gráfica: http://www.analyzemath.com/high_school_math/grade_12/sinus_applications/question_7_sol_1.gif)
-
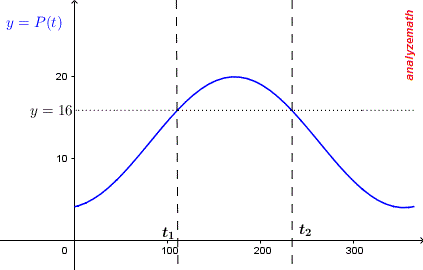
Hay una diferencia de medio período entre el máximo en \( t = 172 \) y el mínimo después de ese máximo. Por lo tanto, \( P(t) \) es mínima en:
\[
t = 172 + 0.5(365) = 354.5
\]
Los primeros 11 meses tienen 334 días. Por lo tanto, 354.5 corresponde al 21 de diciembre, el día en que \( P(t) \) es mínima.
-
Para encontrar el número de días durante los cuales la potencia producida es suficiente, necesitamos encontrar \( t_1 \) y \( t_2 \) correspondientes a los puntos de intersección de \( P(t) \) y \( y = 16 \), como se muestra en la gráfica, resolviendo la ecuación:
\[
P(t) = 16
\]
\[
8 \cos\left(\frac{2\pi}{365}(t - 172)\right) + 12 = 16
\]
\[
\cos\left(\frac{2\pi}{365}(t - 172)\right) = \frac{1}{2}
\]
\[
t = 172 + \frac{365}{2\pi} \arccos\left(\frac{1}{2}\right) = 232.8
\]
La solución encontrada anteriormente es mayor que 172, correspondiente al máximo. Por lo tanto, la solución anterior corresponde a \( t_2 \) en la gráfica (solución del lado derecho). La solución del lado izquierdo se encuentra por simetría:
\[
t_1 = 172 - (232.8 - 172) = 111.2
\]
\[
t_2 - t_1 = 232.8 - 111.2 = 121.6 \text{ días}
\]
El sistema produce suficiente potencia durante aproximadamente 121 días.
Referencias
