Problemas y Preguntas de Trigonometría con Soluciones - Grado 12

Comenzamos con el lado izquierdo de la identidad dada. Usamos la identidad \( \tan(x) = \dfrac{\sin(x)}{\cos(x)} \) en el lado izquierdo: \[ \tan^2(x) - \sin^2(x) = \left(\dfrac{\sin(x)}{\cos(x)}\right)^2 - \sin^2(x) \] \[ = \dfrac{\sin^2(x)}{\cos^2(x)} - \sin^2(x) \] \[ = \dfrac{\sin^2(x) - \cos^2(x) \sin^2(x)}{\cos^2(x)} \] \[ = \dfrac{\sin^2(x) \left(1 - \cos^2(x)\right)}{\cos^2(x)} \] \[ = \dfrac{ \sin^2(x) \sin^2(x)}{\cos^2(x)} \] \[ = \sin^2(x) \tan^2(x) \] que es igual al lado derecho de la identidad dada.

Usamos las identidades \( \cos(2x) = 2 \cos^2(x) - 1 \) y \( \sin(2x) = 2 \sin(x) \cos(x) \) en el lado izquierdo: \[ \dfrac{1 + \cos(x) + \cos(2x)}{\sin(x) + \sin(2x)} \] \[ = \dfrac{1 + \cos(x) + 2 \cos^2(x) - 1}{\sin(x) + 2 \sin(x) \cos(x) } \] \[ = \dfrac{\cos(x) + 2 \cos^2(x)}{\sin(x) + 2 \sin(x) \cos(x) } \] \[ = \dfrac{\cos(x) (1 + 2 \cos(x))}{\sin(x) (1 + 2 \cos(x)) } \] \[ = \dfrac{\cos(x)}{\sin(x)} = \cot(x) \] que es igual al lado derecho.

Usamos la identidad \( \sin(2x) = 2 \sin(x) \cos(x) \) para escribir \( \sin(4x) = 2 \sin(2x) \cos(2x) \) en el lado derecho: \[ \dfrac{\sin(4x)}{\cos(2x)} = \dfrac{2 \sin(2x) \cos(2x)}{\cos(2x)} \] \[ = 2 \sin(2x) \] \[ = 2 \times 2 \sin(x) \cos(x) = 4 \sin(x) \cos(x) \] que es igual al lado izquierdo.

Usamos la identidad \( \sin(x) = \sin(2 (x/2)) = 2 \sin(x/2) \cos(x/2) \): \[ 2 \sin(x/2) \cos(x/2) + \sin(x/2) = 0 \] Factorizamos \( \sin(x/2) \): \[ \sin(x/2) (2 \cos(x/2) + 1) = 0 \] Esto da dos ecuaciones: \[ \sin(x/2) = 0 \quad \text{y} \quad 2 \cos(x/2) + 1 = 0 \] a) \( \sin(x/2) = 0 \) tiene soluciones \( x/2 = 0 \) y \( x/2 = \pi \). Resolviendo: \( x = 0 \) y \( x = 2\pi \). b) \( 2 \cos(x/2) + 1 = 0 \) se escribe como \( \cos(x/2) = -1/2 \), con soluciones \( x/2 = 2\pi/3 \) y \( x/2 = 4\pi/3 \). Resolviendo: \( x = 4\pi/3 \) y \( x = 8\pi/3 \). Nota: \( 8\pi/3 > 2\pi \), por lo que no se acepta. Soluciones finales: \( \{ 0, 4\pi/3, 2\pi \} \).

La ecuación ya está factorizada: \[ (2\sin(x) - 1)(\tan(x) - 1) = 0 \] Esto implica: \[ 2\sin(x) - 1 = 0 \quad \text{y} \quad \tan(x) - 1 = 0 \] Es decir: \[ \sin(x) = 1/2 \quad \text{y} \quad \tan(x) = 1 \] Soluciones de \( \sin(x) = 1/2 \): \( x = \pi/6 \) y \( x = 5\pi/6 \). Soluciones de \( \tan(x) = 1 \): \( x = \pi/4 \) y \( x = 5\pi/4 \). Soluciones dentro del intervalo: \( \{\pi/6, 5\pi/6, \pi/4, 5\pi/4\} \).

Usamos la fórmula para \( \cos(A+B) \): \[ \cos(3x) = \cos(2x + x) = \cos(2x) \cos(x) - \sin(2x) \sin(x) \] Así, la ecuación se convierte en: \[ \cos(3x) = 0 \] Resolvemos para \( 3x \): \[ 3x = \pi/2, 3\pi/2, 5\pi/2, 7\pi/2, 9\pi/2, 11\pi/2 \] Soluciones para \( x \): \[ \{\pi/6, \pi/2, 5\pi/6, 7\pi/6, 3\pi/2, 11\pi/6\} \]

Usamos las identidades \( \sin(2x) = 2 \sin(x) \cos(x) \) y \( \cos(2x) = 1 - 2 \sin^2(x) \): \[ \dfrac{\sin(2x) - \cos(x)}{\cos(2x) + \sin(x) - 1} = \dfrac{2 \sin(x) \cos(x) - \cos(x)}{1 - 2 \sin^2(x) + \sin(x) - 1} \] Simplificamos: \[ = \dfrac{\cos(x)(2 \sin(x) - 1)}{\sin(x)(-2 \sin(x) + 1)} \] \[ = - \dfrac{\cos(x)}{\sin(x)} = - \cot(x) \]

Escribimos \( 105^{\circ} = 60^{\circ} + 45^{\circ} \). Usamos la identidad \( \sin(a+b) = \sin(a)\cos(b) + \cos(a)\sin(b) \): \[ \sin(105^{\circ}) = \sin(60^{\circ})\cos(45^{\circ}) + \cos(60^{\circ})\sin(45^{\circ}) \] Con valores conocidos: \[ = \left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{2}}{2}\right) + \left(\frac{1}{2}\right)\left(\frac{\sqrt{2}}{2}\right) \] \[ = \frac{\sqrt{6} + \sqrt{2}}{4} \]

Dado \( \sin(x) = 2/5 \), entonces \( \cos(x) = \sqrt{1 - \sin^2 x} = \sqrt{1 - (2/5)^2} = \sqrt{21}/5 \).

1. \( \cos(2x) = 1 - 2 \sin^2(x) = 1 - 2(4/25) = 17/25 \)
2. \( \cos(4x) = 1 - 2 \sin^2(2x) = 1 - 2[2\sin(x)\cos(x)]^2 = 1 - 2[2\cdot(2/5)\cdot(\sqrt{21}/5)]^2 = 457/625 \)
3. \( \sin(2x) = 2 \sin(x) \cos(x) = 2\cdot(2/5)\cdot(\sqrt{21}/5) = 4\sqrt{21}/25 \)
4. \( \sin(4x) = 2 \cos(2x) \sin(2x) = 2\cdot(17/25)\cdot(4\sqrt{21}/25) = 136\sqrt{21}/625 \)

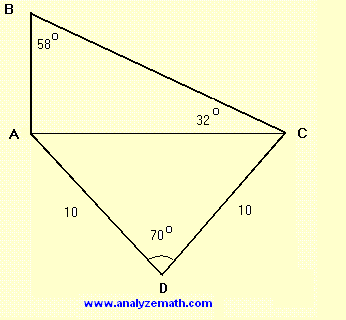
El triángulo \( DAC \) es isósceles. Al trazar la perpendicular desde D a AC, esta corta AC en dos mitades y bisecta el ángulo D. Usando el triángulo rectángulo cuya hipotenusa es AD: \[ (1/2) AC = 10 \sin(35^{\circ}) \Rightarrow AC = 20 \sin(35^{\circ}) \] En el triángulo ABC, los ángulos internos B y C suman \( 90^{\circ} \), por lo que el tercer ángulo es recto. Entonces: \[ \tan(32^{\circ}) = AB / AC \Rightarrow AB = AC \tan(32^{\circ}) \] \[ = 20 \sin(35^{\circ})\tan(32^{\circ}) \approx 7.17 \]