Calcular Áreas de Cuadrados, Rectángulos, Triángulos,
Paralelogramos y Trapecios - Grado 6
Ejemplos y problemas de 6º grado para calcular áreas de rectángulos, cuadrados, triángulos, paralelogramos y trapecios con soluciones detalladas y explicaciones.
Fórmulas para Calcular Áreas
Se presentan las fórmulas para calcular las áreas de rectángulos, cuadrados, triángulos, paralelogramos y trapecios.
|

Rectángulo: Área = L × W
|

Cuadrado: Área = S × S = S 2
|
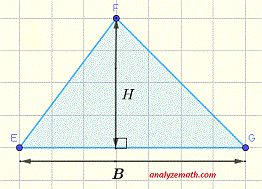
Triángulo: Área = (1 / 2) × H × B
|
|

Paralelogramo: Área = L × H
|

Trapecio: Área = (1 / 2) × H × (B1 + B2)
|
|
Responde las Siguientes Preguntas
-
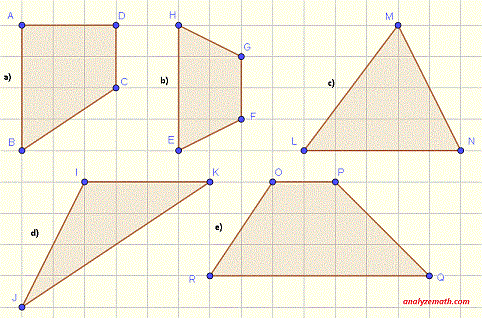
Usa la cuadrícula para determinar las dimensiones de las figuras a continuación y luego utiliza las fórmulas para calcular sus áreas.

-
Determina las dimensiones de las figuras a continuación y luego calcula sus áreas.
Soluciones a los Problemas Anteriores
-
Solución
Primero determinamos las dimensiones necesarias para calcular el área y luego usamos las fórmulas para cada figura.
- La figura en la parte a) es un rectángulo de ancho AD = 3 unidades y largo DC = 4 unidades. Por lo tanto, el área está dada por
Área = Largo × ancho = 4 × 3 = 12 unidades 2
- La figura en la parte b) es un cuadrado de lado HG = 3 unidades. Por lo tanto, el área está dada por
Área = Lado × Lado = 3 × 3 = 9 unidades 2
- La figura en la parte c) es un triángulo rectángulo de altura H = ML = 3 y base B = MN = 4. El área está dada por
Área = (1 / 2) × H × B = (1 / 2) × 3 × 4 = 6 unidades 2
- La figura en la parte d) es un triángulo rectángulo con las mismas dimensiones que el triángulo rectángulo de la parte c): Altura H = IJ = 3 y base B = JK = 4. El área está dada por
Área = (1 / 2) × H × B = (1 / 2) × 3 × 4 = 6 unidades 2
- La figura en la parte e) es un paralelogramo de longitud L = OP = 5 unidades y la distancia H entre OP y RQ = 3 unidades (ver figura a continuación). El área está dada por

Área = L × H = 5 × 3 = 15 unidades 2
Nota que H es perpendicular tanto a OP como a RQ.
-
Solución
Primero necesitamos identificar la figura, determinar sus dimensiones y luego calcular el área.
- La figura en la parte a) es un trapecio con AB y DC paralelos. Base B1 = DC = 2 unidades, base B2 = AB = 4 y la altura H = AD = 3 unidades. Por lo tanto, el área está dada por
Área = (1 / 2) × H × (B1 + B2) = (1 / 2) × 3 × (2 + 4) = (1 / 2) × 3 × 6 = (1 / 2) × 18 = 18 / 2 = 9 unidades 2
- La figura en la parte b) es un trapecio con GF y HE paralelos. Base B1 = GF = 2 unidades, base B2 = HE = 4 y la altura H = 2 unidades. Por lo tanto, el área está dada por
Área = (1 / 2) × H × (B1 + B2) = (1 / 2) × 2 × (2 + 4) = (1 / 2) × 2 × 6 = (1 / 2) × 12 = 12 / 2 = 6 unidades 2
- La figura en la parte c) es un triángulo de base B = LN = 5 unidades y altura H = 4 unidades (ver figura a continuación). El área está dada por

Área = (1 / 2) × B × H = (1 / 2) × 5 × 4 = (1 / 2) × 20 = 20 / 2 = 10 unidades 2
- La figura en la parte d) es un triángulo de base B = IK = 4 unidades y altura H = 4 unidades (ver figura a continuación). El área está dada por

Área = (1 / 2) × B × H = (1 / 2) × 4 × 4 = (1 / 2) × 16 = 16 / 2 = 8 unidades 2
- La figura en la parte e) es un trapecio con base B1 = OP = 2 unidades, base B2 = RQ = 7 unidades y altura H = 3. El área está dada por
Área = (1 / 2) × H × (B1 + B2) = (1 / 2) × 3 × (2 + 7) = (1 / 2) × 3 × 9 = (1 / 2) × 27 = 27 / 2 = 13.5 unidades 2




