Prueba de Práctica de Matemáticas - Grado 6

Se presentan preguntas de práctica de matemáticas de sexto grado junto con sus soluciones.

1 - Números

1. ¿Cuál de las siguientes propiedades
   a) asociativa      b)   conmutativa      c)   distributiva      d)   identidad de la suma      e)   identidad de la multiplicación
   se utiliza para escribir las siguientes igualdades?
   1. \[(5 + 4) + 1 = 5 + (4 + 1)\]
   2. \[2(4 + 7) = 2 \times 4 + 2 \times 7\]
   3. \[11 + 9 = 9 + 11\]
   4. \[33 + 0 = 33\]
   5. \[5 \times 1 = 5\]
   6. \[9 \times 6 = 6 \times 9\]
   7. \[(7 - 2)6 = 7 \times 6 - 2 \times 6\]
   8. \[3 \times 6 - 3 \times 2 = 3(6 - 3)\]
2. ¿Cuáles de los siguientes números son primos?
   \[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 \]
3. ¿En qué valor posicional se encuentra el \(2\) en el número \(1296\)?
4. Evalúa las expresiones
   1. \[(9 - 3) + 2\]
   2. \[7 - (5 - 2)\]
   3. \[(3 + 7) \times 3\]
   4. \[(8 - 2) \times 3\]
5. ¿Qué dígito está en el lugar de las décimas en el número \(12.83\)?
6. Redondea al número entero más cercano.
   1. 0.41
   2. 1.2999
   3. 123.5
7. ¿Cuál de las siguientes afirmaciones es verdadera?
   1. 0.1 > 0.3
   2. 1.2 < 1.3
   3. 0.5 < 0.05
8. Evalúa las siguientes expresiones
   1. \[\mathbf{0.4 \times 3}\]
   2. \[\mathbf{8 - 3 \times 0.2}\]
   3. \[\mathbf{0.5 \div 5}\]

2 - Factores, Múltiplos y Divisibilidad de Números

9. ¿Cuál es el Máximo Común Divisor (MCD) de \(8\) y \(12\)?
10. ¿Cuál es el Mínimo Común Múltiplo (MCM) de \(3\) y \(7\)?
11. ¿Cuál de los siguientes números es divisible por \(5\)?
    1. \(125\)
    2. \(123\)
    3. \(200\)
12. ¿Cuál de los siguientes números es divisible por \(2\)?
    1. \(35\)
    2. \(280\)
    3. \(476\)
13. ¿Cuál de los siguientes números es divisible por \(3\)?
    1. \(105\)
    2. \(101\)
    3. \(234\)

3 - Fracciones y Números Mixtos

14. ¿Cuáles de las siguientes son fracciones impropias?
    1. \(\dfrac{2}{5}\)
    2. \(\dfrac{10}{3}\)
    3. \(\dfrac{3}{3}\)
15. Convierte las siguientes fracciones impropias a números mixtos.
    1. \(\dfrac{7}{5}\)
    2. \(\dfrac{8}{3}\)
    3. \(\dfrac{9}{2}\)
16. Encuentra el numerador o denominador faltante que hace que cada par de fracciones sea equivalente.
    1. \(\dfrac{1}{2} = \dfrac{?}{4}\)
    2. \(\dfrac{2}{5} = \dfrac{6}{?}\)
    3. \(\dfrac{1}{3} = \dfrac{?}{9}\)
17. Evalúa las siguientes expresiones (no es necesario simplificar la respuesta final).
    1. \(\dfrac{4}{10} - \dfrac{1}{10}\)
    2. \(\dfrac{1}{2} + \dfrac{3}{4}\)
    3. \(\dfrac{1}{2} \times \dfrac{2}{3}\)
    4. \(\dfrac{3}{4} \div \dfrac{1}{2}\)
    5. \(\dfrac{3}{4} \div 3\)
    6. \(2 \times \dfrac{2}{6}\)
    7. \(1\dfrac{1}{4} + 2\dfrac{1}{4}\)
    8. \(3\dfrac{2}{5} - 1\dfrac{1}{5}\)
18. Escribe como decimal
    1. \(\dfrac{7}{10}\)
    2. \(\dfrac{17}{100}\)
19. En los diagramas a continuación, un círculo o cuadrado completo es una unidad. Representa cada una de las partes coloreadas (en rojo) como una fracción o un número mixto.
    a)
    
    b)
    
    c)
    

4 - Exponentes

20. Reescribe las siguientes expresiones usando exponentes.
    1. \(2 \times 2 \times 2 \times 2 \times 2\)
    2. Cinco al cuadrado
    3. \(4\) al cubo
    4. \(6\) a la séptima potencia
21. Evalúa las siguientes expresiones
    1. \(2^3\)
    2. \(1^5\)
    3. \(4^2\)
    4. \(1000^0\)

5 - Razones y Tasas

22. Hay \(2\) pelotas rojas y \(3\) pelotas azules en una bolsa. ¿Cuál es la razón de
    1. pelotas rojas a azules?
    2. pelotas azules a rojas?
    3. pelotas azules al número total de pelotas?
23. Hay \(11\) niñas y \(8\) niños en una clase. ¿Cuál es la razón de
    1. niñas a niños?
    2. niños al número total de estudiantes?
24. Sam compró \(5\) kilogramos de tomates a un costo de \(\$15\). Encuentra la tasa unitaria (o precio) en dólares/kilogramo.
25. Un automóvil viajó \(120\) kilómetros (km) en \(2\) horas (hrs). Encuentra la tasa unitaria en km/hr.
26. Hay \(600\) estudiantes en una escuela y la razón de niños a niñas es igual a \(1:3\). ¿Cuántos niños hay en esta escuela?

6 - Porcentajes y Problemas Relacionados

27. ¿Cuánto es el \(60\%\) de \(20\)?
28. Escribe \(35\%\) como un número decimal.
29. Escribe \(15\%\) como una fracción reducida.
30. ¿Cuánto es el \(50\%\) de \(\dfrac{1}{4}\)?
31. Escribe la fracción \(\dfrac{3}{5}\) como un porcentaje.
32. Amanda tiene un salario mensual de \(\$3000\). Gasta \(\$600\) por mes en ropa. ¿Qué porcentaje de su salario mensual gasta Amanda en ropa?
33. El precio de un artículo cambió de \(\$125\) a \(\$100\). ¿Cuál fue el cambio en porcentaje?
34. Una camisa cuesta inicialmente \(\$40\) y ha sido descontada en un \(40\%\). ¿Cuál es el precio de la camisa después del descuento?

7 - Convertir Unidades de Medida

35. ¿Cuántos hectolitros (\(\text{hL}\)) hay en \(320\) litros (\(\text{L}\)) sabiendo que \(1 \text{ hL} = 100 \text{ L}\)?
36. ¿Cuántos metros (\(\text{m}\)) hay en \(234500\) milímetros (\(\text{mm}\)) sabiendo que \(1 \text{ m} = 1000 \text{ mm}\)?
37. ¿Cuántos kilómetros (\(\text{km}\)) hay en \(2300\) metros (\(\text{m}\)) sabiendo que \(1 \text{ km} = 1000 \text{ m}\)?
38. ¿Cuántos mililitros (\(\text{mL}\)) hay en \(1.2\) litros (\(\text{L}\)) sabiendo que \(1 \text{ L} = 1000 \text{ mL}\)?
39. ¿Cuántas horas (\(\text{hrs}\)) hay en \(7200\) segundos (\(\text{sec}\)) sabiendo que \(1 \text{ hr} = 3600 \text{ sec}\)?
40. ¿Cuántas millas (\(\text{mi}\)) hay en \(2640\) yardas (\(\text{yd}\)) sabiendo que \(1 \text{ mi} = 1760 \text{ yd}\)?
41. ¿Cuántas pulgadas (\(\text{in}\)) hay en \(3\) metros (\(\text{m}\)) sabiendo que \(1 \text{ m} = 39.37 \text{ in}\)?

8 - Expresiones Matemáticas

42. Evalúa la expresión \(x + 2\) para \(x = 0.2\)
43. Evalúa la expresión \(2(x + 2)\) para \(x = 3\)
44. Evalúa la expresión \(a - b\) para \(a = 3\) y \(b = 2\)
45. Evalúa la expresión \(\dfrac{2x}{3}\) para \(x = 6\)
46. Escribe expresiones y ecuaciones matemáticas para
    1. \(3\) menos que \(x\)
    2. \(5\) veces \((x+2)\)
    3. \((2x + 1)\) al cuadrado
    4. La suma de \(x\) y \(1\) multiplicada por \(3\) es igual a \(2\).
47. Escribe desigualdades matemáticas para
    1. \(3\) es menor que \(x\)
    2. \(5\) es al menos \(x\)
    3. \(y\) es como máximo \(9\)
    4. La diferencia de \(x\) y \(2\) es menor o igual a \(-2\).
48. Expande los paréntesis y simplifica.
    1. \(2(x + 4)\)
    2. \(3(a + b + 2)\)
    3. \(\dfrac{1}{4}(8x + 4)\)
    4. \(0.2(x + 2)\)
49. Factoriza las expresiones
    1. Encuentra el Máximo Común Divisor (MCD) de \(9\) y \(6\)
    2. Escribe \(9\) y \(6\) como un producto del MCD encontrado en a) y otro número.
    3. Escribe \(9x + 6\) como el producto del MCD encontrado en a) y una expresión entre paréntesis.

9 - Ecuaciones con Una Variable y Problemas Relacionados

50. Resuelve las ecuaciones
    1. \(x + 2 = 8\)
    2. \(2x = 6\)
    3. \(x - 3 = 7\)
51. El perímetro de un jardín rectangular es \(10\) metros y su longitud es \(3\) metros. Sea \(x\) el ancho del jardín.
    1. Escribe una ecuación en \(x\) para resolver el ancho.
    2. Resuelve la ecuación obtenida en la parte a).
    3. Verifica tu respuesta al problema.

10 - Plano de Coordenadas

52. Identifica el cuadrante o eje en un plano de coordenadas de cada punto sin graficarlos.
    1. \((0,1)\)
    2. \((-2,-3)\)
    3. \((2,9)\)
    4. \((-4,6)\)
    5. \((3,-4)\)
    6. \((-3,0)\)
53. Determina las coordenadas de los puntos en el plano de coordenadas a continuación.
    
54. John camina a una velocidad constante de 5 kilómetros por hora (km/hr).
    a) Completa la tabla a continuación donde \(d\) es la distancia, en kilómetros (km), caminada y \(t\) es el tiempo, en horas (hrs), tomado para caminar la distancia \(d\).
    
    b) Grafica los puntos en el plano de coordenadas y une los puntos obtenidos.
    

11 - Desigualdades

55. Representa los números \(-4, 0, 5, -6, 4\) en una recta numérica y decide cuál de las siguientes afirmaciones es verdadera.
    1. \(-4 \lt 0\)
    2. \(0 > 4\)
    3. \(-6 \lt -4\)
    4. \(-6 > 5\)
    5. \(0 \lt 6\)

12 - Geometría

56. Selecciona la respuesta correcta. La suma de todos los ángulos internos de un triángulo es igual a
    1. \(360^{\circ}\).
    2. \(180^{\circ}\).
    3. \(270^{\circ}\).
57. Selecciona la respuesta correcta. Dos líneas rectas se intersectan en el punto \(O\). En la figura a continuación, los ángulos \(\angle AOB\) y \(\angle BOC\) son
    1. Complementarios.
    2. Suplementarios.
    3. Ni complementarios ni suplementarios.
    
58. Tres líneas rectas se intersectan en el punto \(O\). ¿Cuáles de estos pares de ángulos son opuestos por el vértice?
    1. \(\angle AOB \; \text{y} \; \angle DOF\)
    2. \(\angle BOC \; \text{y} \; \angle EOF\)
    3. \(\angle COD \; \text{y} \; \angle FOB\)
    4. \(\angle FOB \; \text{y} \; \angle COE\)
    5. \(\angle AOC \; \text{y} \; \angle DOE\)
    6. \(\angle BOD \; \text{y} \; \angle EOA\)
    
59. Indica el número de lados de cada una de las figuras geométricas listadas a continuación.
    1. Pentágono
    2. Trapecio
    3. Triángulo
    4. Cometa
60. ¿Cuál de las siguientes afirmaciones es verdadera sobre un triángulo isósceles?
    1. Dos de sus ángulos son iguales pero los tres lados no son iguales.
    2. Dos ángulos son iguales y los lados opuestos a los ángulos iguales son iguales.
    3. Dos lados son iguales pero todos los ángulos son diferentes.
61. Calcula el perímetro de un rectángulo con una longitud de \(10\) cm y un ancho de \(5\) cm.
62. Calcula el área de un círculo con un radio de \(1\) m.
63. ABCD es un rectángulo limitado en el lado izquierdo por el segmento AE. Encuentra el área de la superficie sombreada (en azul) dado que la longitud del segmento DE es igual a 2 cm. (La figura no está a escala)
    

13 - Figuras Tridimensionales

64. Determina el número de aristas y caras de la pirámide truncada mostrada a continuación.
    
65. Dado el prisma rectangular a continuación,
    
    
    1. Encuentra el área de los rectángulos ABCD, ADHE y DCGH.
    2. Encuentra el área superficial del prisma rectangular.
    3. Encuentra el volumen del prisma rectangular.
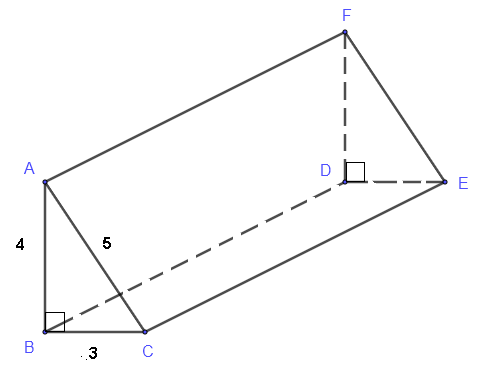
66. Dado que el volumen del prisma triangular a continuación es \(24\), encuentra su área superficial total.
    

14 - Datos y Gráficos

67. El número de horas que Harry pasó entrenando para su partido de fútbol durante 5 días de la semana se muestra en el gráfico de líneas a continuación.
    ¿Cuántas horas pasó Harry entrenando para su partido durante la semana?
    
68. El número de estudiantes (en el eje vertical) y el rango de puntajes (en el eje horizontal) en un examen de inglés se muestran en el histograma a continuación.
    1. ¿Cuántos estudiantes obtuvieron un puntaje en el rango 90-99?
    2. ¿Cuántos estudiantes más obtuvieron un puntaje en el rango 80-89 que estudiantes que obtuvieron un puntaje en el rango 60-69?
    

15 - Estadística

69. Calcula el rango, media, moda y mediana del conjunto de datos: \(\{1, 4, 2, 2, 3, 2, 7\}\).

16 - Probabilidades

70. ¿Cuál de los siguientes no puede ser una medida de probabilidad?
    1. 1
    2. -0.5
    3. 2
    4. 0
    5. 0.0001
71. 1. ¿Cuántos resultados son posibles si lanzas una moneda?
    2. ¿Cuántos resultados son posibles si seleccionas una de cinco cartas diferentes al azar?
    3. ¿Cuántos resultados son posibles si lanzas una moneda y seleccionas una de cinco cartas diferentes al azar?
72. 1. ¿Cuáles son todos los resultados posibles si lanzas un dado justo con números del 1 al 6 en las 6 caras?
    2. Cuando lanzas un dado justo, con números del 1 al 6 en las caras, ¿cuál es la probabilidad de que
       1. el número obtenido sea igual a 0?
       2. el número obtenido sea igual a 5?
       3. el número obtenido sea mayor que 4?

Más Referencias y Enlaces

• Problemas y Preguntas de Fracciones con Soluciones
• Matemáticas de Secundaria (Grados 6, 7, 8, 9) - Preguntas y Problemas Gratuitos con Respuestas
• Matemáticas de Bachillerato (Grados 10, 11 y 12) - Preguntas y Problemas Gratuitos con Respuestas
• Matemáticas Primarias (Grados 4 y 5) con Preguntas y Problemas Gratuitos con Respuestas