Problemas de Matemáticas con Soluciones para 6º Grado
Problemas de matemáticas de 6º grado que cubren una amplia gama de temas, incluyendo fracciones, porcentajes, MCD, MCM, razones, ecuaciones, distancia-tiempo-velocidad y geometría (rectángulos, cuadrados, círculos), así como ángulos en triángulos. Se presentan con soluciones detalladas y explicaciones completas. Se incluyen algunos problemas desafiantes.
Pregunta 1
Una secuencia sigue la regla: Comienza en 2, y multiplica por 3 y suma 2 cada vez. ¿Cuál es el quinto número en la secuencia?
Secuencia:
1º : 2
2º : \(2 \times 3 + 2 = 8\)
3º : \(8 \times 3 + 2 = 26\)
4º : \(26 \times 3 + 2 = 80\)
5º : \(80 \times 3 + 2 = 242\)
El quinto número es \( 242\).
Pregunta 2
Se recorta un cuadrado de 2 cm de lado de cada esquina de un cartón rectangular que mide 12 cm de largo y 8 cm de ancho. ¿Cuál es el área del cartón después de quitar los cuatro cuadrados?
Área original del cartón: \[ \text{Área} = \text{largo} \times \text{ancho} = 12 \times 8 = 96 \, \text{cm}^2 \] Área de un cuadrado recortado: \[ \text{Área} = 2 \times 2 = 4 \, \text{cm}^2 \] Área total removida de las cuatro esquinas: \[ 4 \times 4 = 16 \, \text{cm}^2 \] Área restante después del recorte: \[ 96 - 16 = 80 \, \text{cm}^2 \]
Pregunta 3
Dos números \( N \) y 16 tienen un mínimo común múltiplo (MCM) de 48 y un máximo común divisor (MCD) de 8. Encuentra el valor de \( N \).
El producto de dos enteros es igual al producto de su MCM y MCD. Por lo tanto, \[ 16 \times N = 48 \times 8 \] Resolviendo para \( N \): \[ N = \dfrac{48 \times 8}{16} = 24 \]
Pregunta 4
Encuentra el máximo común divisor (MCD) de 24, 40 y 60.
Escribimos la factorización prima de cada número: \[ 24 = 2^3 \times 3 \] \[ 40 = 2^3 \times 5 \] \[ 60 = 2^2 \times 3 \times 5 \] El único factor primo común a los tres es 2. La menor potencia común es \(2^2\). \[ \text{MCD} = 2^2 = 4 \] El máximo común divisor de 24, 40 y 60 es 4.
Pregunta 5
En una escuela, hay 240 niños y 260 niñas.
a) ¿Cuál es la razón entre el número de niñas y el número de niños?
b) ¿Cuál es la razón entre el número de niños y el número total de alumnos?
a) Razón de niñas a niños: \[ \dfrac{260}{240} = \dfrac{13}{12} \] La razón es \( 13:12 \).
b) Total de alumnos: \( 240 + 260 = 500 \)
Razón de niños al total: \[ \dfrac{240}{500} = \dfrac{12}{25} \] La razón es \( 12:25 \).Pregunta 6
Si Tim almorzó por \$50.50 y dio una propina del 20%, ¿cuánto gastó en total?
Propina: \[ 20\% \text{ de } 50.50 = 0.20 \times 50.50 = 10.10 \] Total gastado: \[ 50.50 + 10.10 = 60.60 \] Tim gastó \$60.60 en total.
Pregunta 7
Encuentra \( k \) si \( \dfrac{64}{k} = 4 \).
Reescribimos la división como multiplicación: \[ 64 = 4k \] Entonces: \[ k = \dfrac{64}{4} = 16 \]
Pregunta 8
¿Cuál es \( x \) si \( x + 2y = 10 \) y \( y = 3 \)?
Sustituimos \( y = 3 \): \[ x + 2(3) = 10 \] \[ x + 6 = 10 \] \[ x = 10 - 6 = 4 \]
Pregunta 9
Una compañía telefónica cobra una tarifa inicial de \$0.50 y luego \$0.11 por cada minuto adicional. Escribe una expresión que dé el costo \( C \) de una llamada que dura \( N \) minutos.
El costo es: \[ C = 0.50 + 0.11N \]
Pregunta 11
Un auto recorre 40 kilómetros por galón de gasolina. ¿Cuántos galones de gasolina necesitará el auto para viajar 180 kilómetros?
Número de galones: \[ \dfrac{180}{40} = 4.5 \] El auto necesita 4.5 galones.
Pregunta 12
Una máquina llena 150 botellas de agua cada 8 minutos. ¿Cuántos minutos tardará esta máquina en llenar 675 botellas?
Número de grupos de 150 botellas en 675: \[ \dfrac{675}{150} = 4.5 \] Tiempo requerido: \[ 4.5 \times 8 = 36 \text{ minutos} \]
Pregunta 13
Un auto viaja a una velocidad de 65 millas por hora. ¿Qué distancia recorrerá en 5 horas?
Distancia: \[ 5 \times 65 = 325 \text{ millas} \]
Pregunta 14
Un rectángulo \( A \) con largo 10 cm y ancho 5 cm es similar a otro rectángulo \( B \) cuyo largo es 30 cm. Encuentra el área del rectángulo \( B \).
Por semejanza: \[ \dfrac{30}{10} = \dfrac{W_2}{5} \] \[ W_2 = 15 \text{ cm} \] Área de \( B \): \[ 30 \times 15 = 450 \text{ cm}^2 \]
Pregunta 15
Una escuela tiene 10 clases con el mismo número de estudiantes en cada clase. Un día, 5 clases estuvieron medio llenas, 3 clases estuvieron \(\dfrac{3}{4}\) llenas, y en las últimas 2 clases faltó \(\dfrac{1}{8}\) de los estudiantes. En total faltaron 70 estudiantes. ¿Cuántos estudiantes están registrados en esta escuela?
Sea \( x \) el número de estudiantes por clase.
Estudiantes ausentes en 5 clases: \( 5 \times \frac{x}{2} = \frac{5x}{2} \)
En 3 clases: \( 3 \times \frac{x}{4} = \frac{3x}{4} \)
En 2 clases: \( 2 \times \frac{x}{8} = \frac{2x}{8} \)
Total ausentes: \[ \frac{5x}{2} + \frac{3x}{4} + \frac{2x}{8} = 70 \] Multiplicando por 8: \[ 20x + 6x + 2x = 560 \] \[ 28x = 560 \Rightarrow x = 20 \] Total en la escuela: \( 10 \times 20 = 200 \)Pregunta 16
Un cuadrado grande está formado por 16 cuadrados congruentes. ¿Cuál es el número total de cuadrados de diferentes tamaños que hay?

Cuadrados de \(1\times1\): 16
Cuadrados de \(2\times2\): 9
Cuadrados de \(3\times3\): 4
Cuadrados de \(4\times4\): 1
Total: \(16+9+4+1 = 30\)
Pregunta 17
John dio la mitad de sus estampillas a Jim. Jim luego dio la mitad de sus estampillas a Carla. Carla dio \(\dfrac{1}{4}\) de las estampillas que recibió a Thomas y se quedó con las 12 restantes. ¿Con cuántas estampillas comenzó John?
Sea \( x \) las estampillas de John.
Jim recibe: \( \frac{x}{2} \)
Carla recibe: \( \frac{1}{4}x \)
Carla se queda: \( \frac{3}{4} \times \frac{x}{4} = \frac{3x}{16} = 12 \)
Resolviendo: \( x = 64 \).Pregunta 18
Dos pelotas A y B rotan por una pista circular. La pelota A da 4 rotaciones completas en 120 segundos. La pelota B da 3 rotaciones completas en 60 segundos. Si comienzan a rotar ahora desde el mismo punto, ¿cuánto tiempo tomará para que vuelvan a estar en el punto de partida al mismo tiempo?
Tiempo por rotación de A: \( \frac{120}{4} = 30 \) s
Tiempo por rotación de B: \( \frac{60}{3} = 20 \) s
El primer tiempo común es el MCM de 30 y 20, que es 60 segundos.
Pregunta 19
Un segmento mide 3 unidades de largo. Se divide en 9 partes iguales. ¿Qué fracción de una unidad son 2 partes del segmento?
Cada parte: \( \frac{1}{3} \) de unidad
Dos partes: \( 2 \times \frac{1}{3} = \frac{2}{3} \)
Pregunta 20
Un auto viaja a 75 kilómetros por hora. ¿Cuántos metros recorre el auto en un minuto?
Convertimos: \[ 75 \text{ km/h} = \frac{75 \times 1000 \text{ m}}{60 \text{ min}} = 1250 \text{ m/min} \]
Pregunta 21
Linda gastó \( \dfrac{3}{4} \) de sus ahorros en muebles. Luego gastó \( \dfrac{1}{2} \) de sus ahorros restantes en una nevera. Si la nevera le costó \$150, ¿cuáles eran sus ahorros originales?
Sea \( x \) los ahorros originales.
Después de muebles le queda: \( \frac{x}{4} \)
Gasto en nevera: \( \frac{1}{2} \times \frac{x}{4} = \frac{x}{8} = 150 \)
Resolviendo: \( x = 1200 \).Pregunta 22
El perímetro del cuadrado A es 3 veces el perímetro del cuadrado B. ¿Cuál es la razón del área del cuadrado A al área del cuadrado B?
Sea \( x \) lado de A, \( y \) lado de B. \[ 4x = 3(4y) \Rightarrow x = 3y \] Razón de áreas: \[ \frac{x^2}{y^2} = \frac{(3y)^2}{y^2} = 9 \] La razón es \( 9:1 \).
Pregunta 23
Mary quiere hacer una caja rectangular abierta. Comienza con un cartón de 15 cm de largo y 10 cm de ancho. Luego corta 4 cuadrados congruentes de 3 cm de lado en las cuatro esquinas y dobla por las líneas para hacer la caja. ¿Cuál es el volumen de la caja?
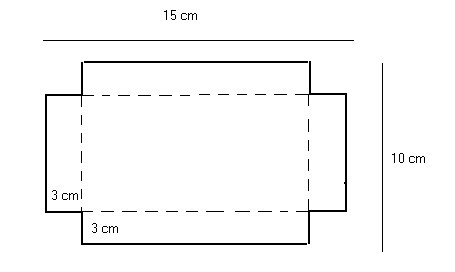
Largo de la caja: \( 15 - 2\times3 = 9 \) cm
Ancho de la caja: \( 10 - 2\times3 = 4 \) cm
Altura: 3 cm
Volumen: \( 9 \times 4 \times 3 = 108 \text{ cm}^3 \)
Pregunta 24
Se corta un cuadrado pequeño de lado \( 2x \) de la esquina de un rectángulo cuyo ancho es 10 cm y largo 20 cm. Escribe una expresión en términos de \( x \) para el área de la figura restante.
Área del rectángulo: \( 20 \times 10 = 200 \)
Área del cuadrado: \( (2x)^2 = 4x^2 \)
Área restante: \( 200 - 4x^2 \)
Pregunta 25
Si el área de un círculo es \( 81 \pi \) pies cuadrados, encuentra su circunferencia.
Área: \( \pi r^2 = 81\pi \Rightarrow r = 9 \)
Circunferencia: \( 2\pi r = 18\pi \) pies
Pregunta 26
Carla tiene 5 años y Jim es 13 años menor que Peter. Hace un año, la edad de Peter era el doble de la suma de las edades de Carla y Jim. Encuentra la edad actual de cada uno.
Sea \( P \) la edad de Peter.
Edades actuales: Carla = 5, Peter = P, Jim = \( P - 13 \).
Hace un año: Carla = 4, Peter = \( P-1 \), Jim = \( P-14 \).
Ecuación:
\[ P-1 = 2(4 + P-14) \Rightarrow P-1 = 2(P-10) \Rightarrow P = 19 \]
Entonces: Peter = 19, Jim = 6, Carla = 5.
Pregunta 27
Lisa corrió 2.4 kilómetros por la mañana y 1.75 kilómetros por la tarde. Quiere correr un total de 6 kilómetros en un día. ¿Cuántos kilómetros más necesita correr para alcanzar su meta?
Ya corrió: \( 2.4 + 1.75 = 4.15 \) km
Le falta: \( 6 - 4.15 = 1.85 \) km
Pregunta 28
Una receta necesita harina y azúcar en la proporción 3:2. Si tienes 4 tazas de azúcar, ¿cuántas tazas de harina necesitas?
Sea \( x \) tazas de harina. \[ \frac{x}{4} = \frac{3}{2} \Rightarrow x = 6 \] Necesitas 6 tazas de harina.
Pregunta 29
Dos ángulos de un triángulo miden \( 47^\circ \) y \( 58^\circ \). ¿Cuál es la medida del tercer ángulo?
Suma de ángulos: \( 180^\circ \)
Tercer ángulo: \( 180 - 47 - 58 = 75^\circ \)
Pregunta 30
Si \( 3x + 4 = 19 \), ¿cuál es el valor de \( x \)?
\[ 3x = 15 \Rightarrow x = 5 \]
Pregunta 31
La temperatura a las 6 AM era \( -4^\circ \) C. Al mediodía, la temperatura había subido \( 11^\circ \). Luego bajó \( 6^\circ \) C para las 6 PM. ¿Cuál era la temperatura a las 6 PM?
Mediodía: \( -4 + 11 = 7^\circ \)
6 PM: \( 7 - 6 = 1^\circ \)
Pregunta 32
Amira compró una chaqueta por \$84 después de un descuento del 30%. ¿Cuál era el precio original?
Sea \( x \) el precio original. \[ 0.70x = 84 \Rightarrow x = 120 \] Precio original: \$120.
Pregunta 33
La distancia entre Harry y Kate es de 2500 metros. Kate y Harry comienzan a caminar uno hacia el otro, y el perro de Kate comienza a correr de un lado a otro entre Harry y Kate a una velocidad de 120 metros por minuto. Harry camina a 40 m/min y Kate a 60 m/min. ¿Qué distancia habrá recorrido el perro cuando Harry y Kate se encuentren?
Velocidad combinada de Harry y Kate: \( 40 + 60 = 100 \) m/min
Tiempo hasta encontrarse: \( \frac{2500}{100} = 25 \) min
Distancia del perro: \( 120 \times 25 = 3000 \) m