Soluciones al Examen de Práctica de Matemáticas de 6º Grado

Soluciones para las preguntas del examen de práctica de matemáticas de 6º grado, presentadas junto con explicaciones detalladas.
Las preguntas deben resolverse sin calculadora, excepto muy pocas.

    1 - Números

    Soluciones


    1. \((5 + 4) + 1 = 5 + (4 + 1)\): asociatividad de la suma
    2. \(2(4 + 7) = 2 \times 4 + 2 \times 7\): distributividad
    3. \(11 + 9 = 9 + 11\): conmutatividad de la suma
    4. \(33 + 0 = 33\): identidad de la suma
    5. \(5 \times 1 = 5\): identidad de la multiplicación
    6. \(9 \times 6 = 6 \times 9\): conmutatividad de la multiplicación
    7. \((7 - 2) \times 6 = 7 \times 6 - 2 \times 6\): distributividad
    8. \(3 \times 6 - 3 \times 2 = 3(6 - 2)\): distributividad al revés (factorización)

  2. \(\color{red}{2,3,5,7,11}\) son números primos.

  3. Centenas

    1. \((9 - 3) + 2 = 6 + 2 = 8\)
    2. \(7 - (5 - 2) = 7 - 3 = 4\)
    3. \((3 + 7) \times 3 = 10 \times 3 = 30\)
    4. \((8 - 2) \times 3 = 6 \times 3 = 18\)

  5. \(8\)

  6. Reglas de redondeo

    Aplicaciones

    1. \(0.41\) redondeado al número entero más cercano es igual a \(\color{red}{0}\) porque el primer dígito después del punto decimal es \(4\), y por lo tanto menor que \(5\) (regla 1 arriba).
    2. \(1.2999\) redondeado al número entero más cercano es igual a \(\color{red}{1}\) porque el primer dígito después del punto decimal es \(2\), y por lo tanto menor que \(5\) (regla 1 arriba).
    3. \(123.5\) redondeado al número entero más cercano es igual a \(\color{red}{124}\) porque el primer dígito después del punto decimal es \(5\), y por lo tanto mayor o igual que \(5\) (regla 2 arriba).

    1. \(0.1 > 0.3\): falso
    2. \(1.2 \lt 1.3\): verdadero
    3. \(0.5 \lt 0.05\): falso

    1. \(0.4 \times 3 = 1.2\)
    2. \(8 - 3 \times 0.2 = 7.4\)
    3. \(0.5 \div 5 = 0.1\)

    9. 2 - Factores, Múltiplos y Divisibilidad de Números

    Soluciones



  11. Regla: Cualquier número con el último dígito a la derecha (valor de posición de las unidades) igual a \(0\) o \(5\) es divisible por \(5\). Por lo tanto,

    \(12\color{red}5\) y \(20\color{red}0\) son divisibles por \(5\).


  12. Regla: Cualquier número con el último dígito a la derecha (valor de posición de las unidades) igual a \(0, 2, 4, 6\) o \(8\) es divisible por \(2\).

    \(28\color{red}0\) y c) \(47\color{red}6\) son divisibles por \(2\).


  13. Regla: Cualquier número cuyos dígitos sumen un número divisible por \(3\) es divisible por \(3\).
    1. La suma de los dígitos en \(105\) está dada por: \(1+0+5 = \color{red}6\) y porque \(\color{red}6\) es divisible por \(3\), el número dado \(105\) es divisible por \(3\).
    2. La suma de los dígitos en \(101\) está dada por: \(1+0+1 = \color{red}2\) y porque \(\color{red}2\) NO es divisible por \(3\), el número dado \(101\) NO es divisible por \(3\).
    3. La suma de los dígitos en \(234\) está dada por: \(2+3+4 = \color{red}9\) y porque \(\color{red}9\) es divisible por \(3\), el número dado \(234\) es divisible por \(3\).

    14. 3 - Fracciones y Números Mixtos

    Soluciones


  14. Definición: Una fracción cuyo numerador es mayor o igual que su denominador es una fracción impropia.

    b) \(\dfrac{10}{3}\) y c) \(\dfrac{3}{3}\) son fracciones impropias.


    1. \(\dfrac{7}{5} = \dfrac{5+2}{5} = \dfrac{5}{5} + \dfrac{2}{5} = 1 \dfrac{2}{5}\)
    2. \(\dfrac{8}{3} = \dfrac{3+3+2}{3} \\~\\ \qquad = \dfrac{3}{3} + \dfrac{3}{3} + \dfrac{2}{3} = 1 + 1+ \dfrac{2}{3} \\~\\ \qquad = 2 \dfrac{2}{3}\)
    3. \(\dfrac{9}{2} = \dfrac{2+2+2+2+1}{2} \\~\\ \qquad = \dfrac{2}{2} + \dfrac{2}{2} + \dfrac{2}{2} + \dfrac{2}{2} + \dfrac{1}{2} \\~\\ \qquad = 1+1+1+1+ \dfrac{1}{2} = 4 \dfrac{1}{2}\)

  16. Regla: Si multiplicamos (o dividimos) el numerador y el denominador de una fracción dada por el mismo número, obtenemos una nueva fracción equivalente a la fracción dada.
    1. Las fracciones dadas tienen denominadores conocidos \(2\) y \(4\): necesitamos multiplicar el denominador \(2\) por \(2\) para obtener el denominador \(4\)
      Por lo tanto,
      Multiplica el numerador y el denominador de la fracción \(\dfrac{1}{2}\) por \(2\) para obtener una fracción equivalente \(\dfrac{1 \times 2}{2 \times 2} = \dfrac{\color{red}2}{4}\)
      Para que los pares de fracciones dados sean equivalentes, el numerador faltante debe ser igual a \(\color{red}2\)
    2. Las fracciones dadas tienen numeradores conocidos \(2\) y \(6\): necesitamos multiplicar el numerador \(2\) por \(3\) para obtener el numerador \(6\)
      Por lo tanto,
      Multiplica el numerador y el denominador de la fracción \(\dfrac{2}{5}\) por \(3\) para obtener una fracción equivalente \(\dfrac{2 \times 3}{5 \times 3} = \dfrac{6}{\color{red}{15}}\)
      Para que los pares de fracciones dados sean equivalentes, el denominador faltante debe ser igual a \(\color{red}{15}\)
    3. Las fracciones dadas tienen denominadores conocidos \(3\) y \(9\): necesitamos multiplicar el denominador \(3\) por \(3\) para obtener el denominador \(9\)
      Por lo tanto,
      Multiplica el numerador y el denominador de la fracción \(\dfrac{1}{3}\) por \(3\) para obtener una fracción equivalente \(\dfrac{1 \times 3}{3 \times 3} = \dfrac{\color{red}3}{9}\)
      Para que los pares de fracciones dados sean equivalentes, el numerador faltante debe ser igual a \(\color{red}3\)

    1. Las fracciones en la expresión tienen el mismo denominador, por lo tanto evaluamos restando los numeradores y manteniendo el mismo denominador de la siguiente manera:
      \(\dfrac{4}{10} - \dfrac{1}{10} = \dfrac{4-1}{10} = \dfrac{3}{10}\)
    2. Reescribe la fracción \(\dfrac{1}{2}\) con el denominador \(4\) multiplicando su numerador y denominador por \(2\)
      \(\dfrac{1}{2} + \dfrac{3}{4} = \dfrac{1 \times 2}{2 \times 2 } + \dfrac{3}{4}\)
      Simplifica
      \(= \dfrac{2}{4} + \dfrac{3}{4}\)
      Ahora que las fracciones tienen el mismo denominador, sumamos los numeradores y evaluamos de la siguiente manera:
      \(= \dfrac{2+3}{4} = \dfrac{5}{4}\)
    3. Regla de multiplicación de fracciones: Multiplica numeradores juntos y denominadores juntos.
      \(\dfrac{1}{2} \times \dfrac{2}{3} = \dfrac{1 \times 2}{2 \times 3}\)
      Simplifica
      \(= \dfrac{2}{6}\)
    4. Regla de división de fracciones: multiplica la primera fracción por el recíproco de la segunda fracción.
      \(\dfrac{3}{4} \div \dfrac{1}{2} = \dfrac{3}{4} \times \dfrac{2}{1}\)
      Aplica la regla de multiplicación de fracciones y simplifica.
      \(= \dfrac{3 \times 2}{4 \times 1} = \dfrac{6}{4}\)
    5. Reescribe \(3\) como una fracción \(3 = \dfrac{3}{1}\)
      \(\dfrac{3}{4} \div 3 = \dfrac{3}{4} \div \dfrac{3}{1}\)
      Usa la regla de división de fracciones
      \(= \dfrac{3}{4} \times \dfrac{1}{3}\)
      Usa la regla de multiplicación de fracciones
      \(= \dfrac{3 \times 1}{4 \times 3} = \dfrac{3}{12}\)
    6. Reescribe \(2\) como una fracción \(2 = \dfrac{2}{1}\)
      \(2 \times \dfrac{2}{6} = \dfrac{2}{1} \times \dfrac{2}{6}\)
      Usa la regla de multiplicación
      \(= \dfrac{4}{6}\)
    7. Suma las partes enteras de los números mixtos y las fracciones por separado
      \(1 \dfrac{1}{4} + 2 \dfrac{1}{4} = (1 + 2) + (\dfrac{1}{4} + \dfrac{1}{4}) = 3 \dfrac{2}{4}\)
    8. Resta las partes enteras de los números mixtos y las fracciones por separado
      \(3 \dfrac{2}{5} - 1 \dfrac{1}{5} = (3-1) + (\dfrac{2}{5} - \dfrac{1}{5}) = 3 \dfrac{1}{5}\)

  18. Escribe como decimal
    1. \(\dfrac{7}{10} = 7 \div 10 = 0.7\)
    2. \(\dfrac{17}{100} = 17 \div 100 = 0.17\)

    1. \(1 \dfrac{1}{4}\)
    2. \(\dfrac{1}{4}\)
    3. \(3 \dfrac{3}{8}\)

4 - Exponentes

Soluciones

    1. \(2 \times 2 \times 2 \times 2 \times 2 = 2^5\)
    2. Cinco al cuadrado: \(5^2\)
    3. \(4\) al cubo: \(4^3\)
    4. \(6\) a la séptima potencia: \(6^7\)

    1. \(2^3 = 2 \times 2 \times 2 = 8\)
    2. \(1^5 = 1 \times 1 \times 1 \times 1 \times 1 = 1\)
    3. \(4^2 = 4 \times 4 = 16\)
    4. \(1000^0 = 1\) (Cualquier número distinto de cero elevado a la potencia \(0\) es igual a \(1\))

    • 5 - Razones y Tasas

    Soluciones

    1. \(2:3\)
    2. \(3:2\)
    3. \(3:5\)

    1. \(11:8\)
    2. \(8:19\)

  • \(\$15 \div 5 \text{kg} = \$3 / \text{kg}\)

  • \(120 \text{km} \div 2 \text{horas} = 60 \text{km} / \text{h}\)

  • La razón de niños a niñas es \(1:3\).

    Si \(x\) es el número de niños del total de \(600\) estudiantes, entonces \(3x\) es el número de niñas del total de \(600\) estudiantes.

    El número total de niños y niñas es \(600\), por lo tanto podemos escribir la ecuación \[ x + 3x = 600 \] Agrupa términos semejantes en el lado izquierdo de la ecuación \[ 4x = 600 \] Divide ambos lados de la ecuación por \(4\) \[ 4x \div 4 = 600 \div 4 \] Simplifica \( x = 600 \div 4 = 150 \) estudiantes son niños.

    Verifica si la respuesta al problema tiene sentido

    El número de niñas es \(3x = 3 \times 150 = 450\). Por lo tanto, el número total de niños y niñas es igual a \(150 + 450 = 600\), que es exactamente lo dado.

    • 6 - Porcentaje y Problemas Relacionados

    Soluciones

  • \(\dfrac{60}{100} \times 20 = \dfrac{60 \times 20}{100} = 12\)

  • \(35\% = \dfrac{35}{100} = 35 \div 100 = 0.35\)

  • \(15\% = \dfrac{15}{100} = \dfrac{15 \div 5}{100 \div 5} = \dfrac{3}{20}\)

  • \(50\% \times \dfrac{1}{4} = \dfrac{50}{100} \times \dfrac{1}{4} = \dfrac{50}{400} = \dfrac{1}{8}\)

  • \(\dfrac{3}{5} = 3 \div 5 = 0.6 = 60 \div 100 = 60\%\)

  • \(\dfrac{600}{3000} = 0.2 = 20 \div 100 = \dfrac{20}{100} = 20\%\) del salario de Amanda se gasta en ropa.

  • cambio en porcentaje \(= \dfrac{\text{precio nuevo - precio original}}{\text{precio original}} = \dfrac{100 - 125}{125} = - 0.2 = - 20\%\)

  • \(40 - 40\% \times 40 = 40 - \dfrac{40}{100} \times 40 = 40 - \dfrac{1600}{100} = 40 - 16 = \$24\) es el precio después del descuento.

    • 7 - Convertir Unidades de Medida

    Soluciones

  • Divide ambos lados de la igualdad dada \(\quad 1 \text{ hl} = 100 \text{ L} \quad\) por \(100\) y simplifica para obtener otra igualdad escrita como \(\quad 1\text{ L} = \dfrac{1}{100} \text{ hl}\)

    Convertimos de la siguiente manera \[ 320 \text{ L} = 320 \times \dfrac{1}{100} \text{ hl} = \dfrac{320}{100} \text{ hl} = 3.2 \text{ hl} \]


  • Divide ambos lados de la igualdad dada \(\quad 1 \text{ m} = 1000 \text{ mm} \quad\) por \(1000\) y simplifica para obtener otra igualdad escrita como \(\quad \dfrac{1}{1000} \text{ m} = 1\text{ mm}\)

    Convertir \[ 234500 \text{ mm} = 234500 \times \dfrac{1}{1000} \text{ m} = \dfrac{234500}{1000} \text{ m} = 234.5 \text{ m}\]


  • Divide ambos lados de la igualdad dada \(\quad 1 \text{ km} = 1000 \text{ m} \quad\) por \(1000\) para obtener la igualdad \(\quad 1 \text{ m} = \dfrac{1}{1000} \text{ km}\)

    Por lo tanto, la conversión \[ 2300 \text{ m} = 2300 \times \dfrac{1}{1000} \text{ km} = 2.3 \text{ km}\]


  • \[ 1.2 \text{ L} = 1.2 \times 1000 \text{ mL} = 1200 \text{ mL} \]

  • Divide ambos lados de la igualdad dada \(\quad 1 \; \text{h} = 3600 \; \text{s} \quad\) por \(3600\) y reescríbela como \[ \quad 1 \text{ s} = \dfrac{1}{3600} \; \text{h} \] Por lo tanto \[ 7200 \text{ s} = 7200 \times \dfrac{1}{3600} \; \text{h} = \dfrac{7200}{3600} \; \text{h} = 2 \text{ h} \]

  • Divide ambos lados de la igualdad dada \(\quad 1 \text{ mi} = 1760 \text{ yd} \quad\) por \(1760\) para obtener la igualdad \[ \quad 1 \text{ yd} = \dfrac{1}{1760} \text{ mi} \] Por lo tanto \[ 2640 \text{ yd} = 2640 \times \dfrac{1}{1760} \text{ mi} = \dfrac{2640}{1760} \text{ mi} = 1.5 \text{ mi} \]

  • \[ 3 \text{ m} = 3 \times 39.37 \text{ in} = 118.11 \text{ in}\]

    • 8 - Expresiones Matemáticas

    Soluciones

  • Sustituye \(x\) por \(0.2\) en la expresión dada \[ \; x + 2 \; = 0.2 + 2 = 2.2 \]

  • Sustituye \(x\) por \(3\) en la expresión dada \[ \; 2 (x + 2) \; = 2 (3 + 2) = 2 (5) = 2 \times 5 = 10 \]


  • Sustituye \(a\) y \(b\) por \(3\) y \(2\) respectivamente en la expresión dada \[ a - b = 3 - 2 = 1 \]


  • Sustituye \(x\) por \(6\) en la expresión dada \[ \; \dfrac{2 x}{3} = \dfrac{2 \times 6}{3} = \dfrac{12}{3} = 4 \]


    1. \(x - 3\)
    2. \(5(x + 2)\)
    3. \((2x + 1)^2\)
    4. \(3(x + 1) = 2\)

    1. \(3 \lt x\)
    2. \(5 \ge x\)
    3. \(y \le 9\)
    4. \(x - 2 \le -2\)

    1. \[ 2(x + 4) = 2 \times x + 2 \times 4 \\[6pt] \qquad = 2x + 8 \]
    2. \[ 3(a + b + 2) = 3 \times a + 3 \times b + 3 \times 2 \\[6pt] \qquad = 3a + 3b + 6 \]
    3. \[ \dfrac{1}{4}(8x + 4) = \dfrac{1}{4} \times 8x + \dfrac{1}{4} \times 4 \\[6pt] \qquad = \dfrac{8}{4} \times x + \dfrac{4}{4} = 2x + 1 \]
    4. \[ 0.2(x + 2) = 0.2 \times x + 0.2 \times 2 \\[6pt] \qquad = 0.2x + 0.4 \]

    1. Factores de \(9\) son: \(1, \color{red}3, 9\)

      Factores de \(6\) son: \(1, 2, \color{red}3, 6\)

      El máximo común divisor (MCD) de \(9\) y \(6\) es \(\color{red}3\)


    2. \(9 = \color{red}3 \times 3\)
      \(6 = \color{red}3 \times 2\)

    3. \(9 x + 6 = \color{red}3 \times 3 \times x + \color{red}3 \times 2\)
      Usa la propiedad distributiva al revés (es decir: \(\color{red}{a \times x + a \times y = a(x+y)}\)) para factorizar la expresión dada.
      \(9 x + 6 = \color{red}3 \times 3 \times x + \color{red}3 \times 2 = \color{red}3 (3 x + 2)\)

    • 9 - Ecuación con Una Variable y Problemas Relacionados

    Soluciones

    1. Dada la ecuación \(x + 2 = 8\)
      Resta \(2\) de ambos lados de la ecuación
      \(x + 2 \color{red}{- 2} = 8 \color{red}{- 2}\)
      Simplifica
      \(x = 6 \quad\) es la solución de la ecuación dada.
    2. Dada la ecuación \(2 x = 6\)
      Divide ambos lados de la ecuación por \(2\)
      \(2 x \color{red}{\div 2} = 6 \color{red}{\div 2}\)
      Simplifica
      \(x = 3 \quad\) es la solución de la ecuación dada.
    3. Dada la ecuación \(x - 3 = 7\)
      Suma \(3\) a ambos lados de la ecuación
      \(x - 3 \color{red}{+3} = 8 \color{red}{+3}\)
      Simplifica
      \(x = 11 \quad\) es la solución de la ecuación dada.

    1. La fórmula del perímetro \(P\) de un jardín rectangular de longitud \(L\) y ancho \(W\) está dada por
      \(P = 2 \times L + 2 \times W\)
      Sustituimos \(L, W\) y \(P\) por los dados \(L = 3\), \(W = x\) y \(P = 10\) en la fórmula anterior
      \(10 = 2 \times 3 + 2 \times x\)
      Simplifica y reescribe como
      \(2 x + 6 = 10\)

    2. Resta \(6\) de ambos lados de la ecuación
      \(2 x + 6 \color{red}{- 6} = 10 \color{red}{- 6}\)
      Simplifica
      \(2 x = 4\)
      Divide ambos lados de la ecuación por \(2\)
      \(2 x \color{red}{\div 2} = 4 \color{red}{\div 2}\)
      Simplifica
      \(x = 2\) es el ancho del jardín rectangular, por lo tanto \(W = 2\)

    3. Una forma de verificar nuestros cálculos es calcular el perímetro del jardín rectangular.
      \(P = 2 \times L + 2 \times W \\ \qquad = 2 \times 3 + 2 \times 2 = 6 + 4 = 10\)
      que corresponde al perímetro dado \(P = 10\).

    • 10 - Plano de Coordenadas

    Soluciones

    1. \((0,1)\) se encuentra en el lado positivo del eje y
    2. \((-2,-3)\) se encuentra en el cuadrante 3
    3. \((2,9)\) se encuentra en el cuadrante 1
    4. \((-4,6)\) se encuentra en el cuadrante 2
    5. \((3,-4)\) se encuentra en el cuadrante 4
    6. \((-3,0)\) se encuentra en el lado negativo del eje x

  • \(A = (-1,1)\)
    \(B = (0,-1)\)
    \(C = (2,0)\)
    \(D = (3,1)\)
    \(E = (-2,-1)\)
    \(F= (3,-2)\)
    \(G = (0,3)\)
    \(H = (0,0)\)

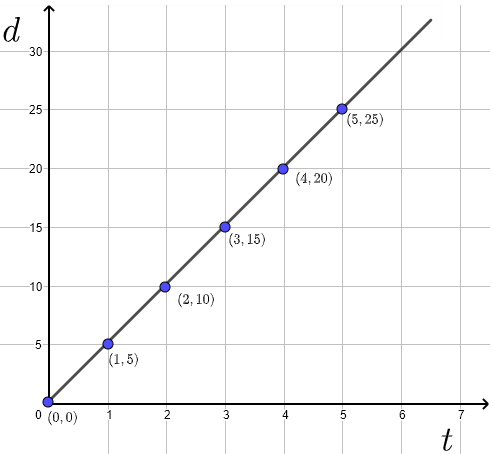
  • a) Para   \(t = 0\), \(d = 0\)
    Para   \(t = 1\) hora, \(d = 5\) km
    Para   \(t = 2 = 1 + 1\) horas, \(d = 5 + 5 = 10\) km
    Para   \(t = 3 = 1 + 1 + 1\) horas, \(d = 5 + 5 + 5 = 15\) km
    Para   \(t = 4 = 1 + 1 + 1 + 1\) horas, \(d = 5 + 5 + 5 + 5 = 20\) km
    Para   \(t = 5 = 1 + 1 + 1 + 1 + 1\) horas, \(d = 5 + 5 + 5 + 5 + 5 = 25\) km

    Tabla de Distancia Versus Tiempo con Valores

    b) Los puntos en la tabla anterior se trazan a continuación y los puntos se unen para dar una línea.

    Plano de Coordenadas con Puntos Trazados

    • 11 - Desigualdades

    Soluciones


  • La recta numérica con los valores involucrados en las desigualdades dadas se muestra a continuación.
    Recta Numérica
    Al comparar dos números usando la recta numérica, el número a la izquierda es menor que el número a la derecha.
    1. \(-4 \lt 0\)     ,     verdadero porque \(-4\) está a la izquierda de \(0\)
    2. \(0 \gt 4\)     ,     falso porque \(0\) está a la izquierda de \(4\)
    3. \(-6 \lt -4\)     ,     verdadero porque \(-6\) está a la izquierda de \(-4\)
    4. \(-6 \gt 5\)     ,     falso porque \(-6\) está a la izquierda de \(5\)
    5. \(0 \lt 6\)     ,     verdadero porque \(0\) está a la izquierda de \(6\)

    • 12 - Geometría

    Soluciones

  • La suma de todos los ángulos internos de un triángulo es igual a
    b) \(180^{\circ}\).


  • En la figura dada, los ángulos \(\angle AOB\) y \(\angle BOC\) son
    b) Suplementarios.

    1. \(\angle AOB \; \text{y} \; \angle DOF \quad\), NO son ángulos verticales
    2. \(\angle BOC \; \text{y} \; \angle EOF \quad\), son ángulos verticales
    3. \(\angle COD \; \text{y} \; \angle FOB\), NO son ángulos verticales
    4. \(\angle FOB \; \text{y} \; \angle COE \quad\), son ángulos verticales
    5. \(\angle AOC \; \text{y} \; \angle DOE \quad\), NO son ángulos verticales
    6. \(\angle BOD \; \text{y} \; \angle EOA\), son ángulos verticales

  •   Da el número de lados de cada una de las figuras geométricas enumeradas a continuación.
    1. Pentágono: 5 lados
    2. Trapecio: 4 lados
    3. Triángulo: 3 lados
    4. Cometa: 4 lados


  • b) Dos ángulos son iguales y los lados opuestos a los ángulos iguales son iguales.


  • \(\text{Perímetro} = 2 \times \text{longitud} + 2 \times \text{ancho} = 2 \times 10 + 2 \times 5 = 20 + 10 = 30\) cm

  • \(\text{Área} = 3.14 \times \text{radio}^2 = 3.14 \times (1)^2 = 3.14\) metros cuadrados.

  • Dado que ABCD es un rectángulo, ADE es un triángulo rectángulo.

    El área de la superficie sombreada se puede calcular restando el área del triángulo rectángulo ADE del área del rectángulo ABCD.

    Área del triángulo rectángulo ADE \(\quad = \dfrac{1}{2} \times \overline{DE} \times \overline{AD} = \dfrac{1}{2} \times 2 \times 7 = 7\) centímetros cuadrados

    Área del rectángulo ABCD \(\quad = \overline{AB} \times \overline{AD} = 10 \times 7 = 70\) centímetros cuadrados

    Área de la superficie sombreada = Área del rectángulo ABCD - Área del triángulo rectángulo ADE \(\quad = 70 - 7 = 63\) centímetros cuadrados

    Nota que la región sombreada cuyo área se calculó anteriormente es un trapecio y su área se puede calcular usando la fórmula para el área de un trapecio.

    • 13 - Figuras Tridimensionales

    Soluciones

  • Número de Aristas \(\quad = 4 + 4 + 4 = 12\)
    Número de Caras \(\quad = 1 + 1 + 4 = 6\)


  • a)

    Área de los rectángulos ABCD \(\quad = 6 \times 4 = 24\) unidades cuadradas
    Área de los rectángulos ADHE \(\quad = 4 \times 10 = 40\) unidades cuadradas
    Área de los rectángulos DCGH \(\quad = 6 \times 10 = 60\) unidades cuadradas

    b)
    El área de la superficie \(A\) del prisma rectangular es igual al DOBLE de la suma de las áreas de los rectángulos ABCD, ADHE y DCGH.
    \(A = 2 \times (24+40+60) = 248\) unidades cuadradas
    c) Volumen \(\quad = 6 \times 4 \times 10 = 240\) unidades cúbicas

  • El volumen está dado por el producto del área \(a\) del triángulo rectángulo ABC y la longitud del prisma \(\overline{AF}\)
    Por lo tanto, la ecuación \[ 24 = a \times \overline{AF} \] El área \(a\) del triángulo rectángulo ABC \(\quad = \dfrac{1}{2} \times 4 \times 3 = 6\)
    Sustituye \(a\) por su valor en la ecuación \[ 24 = 6 \; \overline{AF} \] Divide ambos lados de la ecuación por \(6\) y resuelve para \(\overline{AF}\) para obtener \[ \overline{AF} = 4\] El área de la superficie total está dada por la suma de las áreas de las 5 caras: los dos triángulos rectángulos y los 3 rectángulos
    El área de la superficie total \(\quad = (6 + 6) + (4 \times 4 + 3 \times 4 + 5 \times 4) = 60\) unidades cuadradas

    • 14 - Datos y Gráficos

    Soluciones

  • Número de horas por día
    Lunes: 3 horas
    Martes: 3 horas
    Miércoles: 2 horas
    Jueves: 4 horas
    Viernes: 3 horas
    Número total de horas \(\quad = 3 + 3 + 2 + 4 + 3 = 15\)

  • a) Del histograma, \(3\) estudiantes obtuvieron puntuación en el rango 90-99.
    b) Del histograma, \(7\) estudiantes obtuvieron puntuación en el rango 80-89 y \(4\) estudiantes obtuvieron puntuación en el rango 60-69.
    Por lo tanto, \(7 - 4 = 3\) estudiantes más obtuvieron puntuación en el rango 80-89 que estudiantes que obtuvieron puntuación en el rango 60-69.

    • 15 - Estadística

    Soluciones

  • Valor de dato más grande \(\; = 7\)
    Valor de dato más pequeño \(\; = 1\)
    rango = Valor de dato más grande - Valor de dato más pequeño \(\; = 7 - 1 = 6\)
    media \(\; = \dfrac{1 + 4 + 2 + 2 + 3 + 2 + 7}{7} = \dfrac{21}{7} = 3\)
    moda = el dato con la frecuencia más alta de repetición \(\; = 2\)   (listado 3 veces)
    Ordena los valores de datos de menor a mayor \[ \{ 1 , 2 , 2 , \color{red}2 , 3 , 4 , 7 \} \] la mediana es el valor de dato que se encuentra en el medio (rojo) de los valores de datos ordenados \(\; = 2\)

    • 16 - Probabilidades

    Soluciones

  • La medida de una probabilidad está entre 0 y 1 inclusive. Por lo tanto,
    b) -0.5 y c) 2 no pueden ser medidas de probabilidad.

  • a) \(\color{red}2\) resultados son posibles si lanzas una moneda: cara y cruz
    b)
    \(\color{blue}5\) resultados son posibles si seleccionas una de cinco cartas diferentes al azar.
    c)
    \(\color{red}2 \times \color{blue}5 = 10\) resultados son posibles si lanzas una moneda y seleccionas una de cinco cartas diferentes al azar.


  • a) Si lanzas un dado justo con números del 1 al 6 en las caras, hay \(\color{red}6\) resultados posibles: \(\{ 1 , 2 , 3 , 4 , 5 , 6 \}\)
    b) Es imposible obtener 0 porque no es un resultado posible y por lo tanto la probabilidad es igual a 0.
    c) Hay un 5 entre los 6 resultados, por lo tanto la probabilidad de obtener un número mayor que 4 es igual a \(\color{blue}2 / \color{red}6\)?
    d) Hay \(\color{blue}2\) números mayores que 4 que son 5 y 6, por lo tanto la probabilidad de obtener un número mayor que 4 es igual a \(\color{blue}2 / \color{red}6\)?

    • Más Referencias y Enlaces

    1. Temas de Matemáticas de 6º Grado
    2. Preguntas y Problemas de Fracciones con Soluciones