Problemas de Matemáticas de 7º Grado con Soluciones

Problema 1

En una bolsa llena de pelotas pequeñas, 1/4 son verdes, 1/8 son azules, 1/12 son amarillas y las restantes 26 son blancas. ¿Cuántas pelotas son azules?

Solución:

Definamos el número total de pelotas en la bolsa como $ N $.

Sabemos que:

$ \dfrac{1}{4} $ son verdes: $ \dfrac{N}{4} $

$ \dfrac{1}{8} $ son azules: $ \dfrac{N}{8} $

$ \dfrac{1}{12} $ son amarillas: $ \dfrac{N}{12} $

Las restantes 26 son blancas.

Como todas suman $ N $, podemos escribir:

\[ \dfrac{N}{4} + \dfrac{N}{8} + \dfrac{N}{12} + 26 = N \]

El mínimo común denominador de 4, 8 y 12 es 24. Convirtiendo:

\[ \dfrac{N}{4} = \dfrac{6N}{24}, \quad \dfrac{N}{8} = \dfrac{3N}{24}, \quad \dfrac{N}{12} = \dfrac{2N}{24} \]

Reescribiendo:

\[ \dfrac{6N}{24} + \dfrac{3N}{24} + \dfrac{2N}{24} + 26 = N \] \[ \dfrac{11N}{24} + 26 = N \]

Reorganizando:

\[ 26 = N - \dfrac{11N}{24} = \dfrac{13N}{24} \]

Multiplicando por 24:

\[ 26 \times 24 = 13N \Rightarrow 624 = 13N \Rightarrow N = 48 \]

El número de pelotas azules es:

\[ \dfrac{N}{8} = \dfrac{48}{8} = 6 \]

Problema 2

En una escuela, el $ 50\% $ de los estudiantes son menores de $ 10 $ años, $ \dfrac{1}{20} $ tienen $ 10 $ años, $ \dfrac{1}{10} $ son mayores de $ 10 $ pero menores de $ 12 $, y los restantes $ 70 $ estudiantes tienen $ 12 $ años o más. ¿Cuántos estudiantes tienen $ 10 $ años?

Solución:

Sea $ N $ el total de estudiantes.

$ 50\% $ menores de 10: $ \dfrac{1}{2} N $

$ \dfrac{1}{20} N $ tienen 10 años.

$ \dfrac{1}{10} N $ entre 10 y 12 años.

Restantes 70 estudiantes con 12 años o más.

Ecuación:

\[ \dfrac{1}{2} N + \dfrac{1}{20} N + \dfrac{1}{10} N + 70 = N \]

MCD (2,20,10) = 20:

\[ \dfrac{10}{20} N + \dfrac{1}{20} N + \dfrac{2}{20} N = N - 70 \] \[ \dfrac{13}{20} N = N - 70 \Rightarrow N - \dfrac{13}{20} N = 70 \Rightarrow \dfrac{7}{20} N = 70 \]

Multiplicando por $ \dfrac{20}{7} $:

\[ N = 70 \times \dfrac{20}{7} = 200 \]

Estudiantes de 10 años:

\[ \dfrac{1}{20} \times 200 = 10 \]

Problema 3

Si se duplica la longitud del lado de un cuadrado, ¿cuál es la razón entre el área del cuadrado original y el área del nuevo cuadrado?

Solución:

Sea $ s $ el lado original. Área original: $ A_1 = s^2 $.

Nuevo lado: $ 2s $. Nueva área: $ A_2 = (2s)^2 = 4s^2 $.

Razón:

\[ \dfrac{A_1}{A_2} = \dfrac{s^2}{4s^2} = \dfrac{1}{4} \]

La razón es 1:4.

Problema 4

La división de un número entero $ N $ entre $ 13 $ da un cociente de $ 15 $ y un residuo de $ 2 $. Encuentra $ N $.

Solución:

Usando el algoritmo de división:

\[ N = \text{divisor} \times \text{cociente} + \text{residuo} \]

Sustituyendo:

\[ N = 13 \times 15 + 2 = 195 + 2 = 197 \]

Problema 5

En el rectángulo a continuación, la línea $ M N $ divide el rectángulo en dos regiones. Encuentra $ x $, la longitud del segmento $ N B $, para que el área del cuadrilátero $ M N B C $ sea el $ 40\% $ del área total del rectángulo.

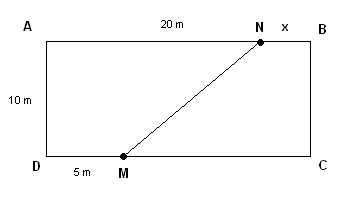
Problema 5

Solución:

Datos: $ AN = 20 $, $ AB = 20 + x $, $ MC = 15 + x $.

Área total del rectángulo:

\[ \text{Área} = (20 + x) \times 10 = 200 + 10x \]

Área de $ MNBC $ (40% del total):

\[ \text{Área de } MNBC = 0.4 \times (200 + 10x) = 80 + 4x \]

Área del trapecio $ MNBC $:

\[ \text{Área} = \dfrac{1}{2} \times 10 \times (x + 15 + x) = 5 \times (2x + 15) \]

Igualando:

\[ 5(2x + 15) = 80 + 4x \] \[ 10x + 75 = 80 + 4x \Rightarrow 6x = 5 \Rightarrow x = \dfrac{5}{6} \text{ m} \]

Problema 6

Una persona trotó $ 10 $ vueltas alrededor de un campo rectangular a razón de $ 12 $ kilómetros por hora durante 30 minutos. Si el campo tiene un largo que es el doble de su ancho, encuentra el área del campo en metros cuadrados.

Solución:

Tiempo: 30 min = 0.5 horas.

Distancia total: $ 12 \times 0.5 = 6 \text{ km} = 6000 \text{ m} $.

Perímetro por vuelta: $ \dfrac{6000}{10} = 600 \text{ m} $.

Ancho = $ w $, Largo = $ 2w $.

Perímetro: $ 2(2w + w) = 600 \Rightarrow 6w = 600 \Rightarrow w = 100 \text{ m} $.

Largo: $ 2w = 200 \text{ m} $.

Área: $ 200 \times 100 = 20000 \text{ m}^2 $.

Problema 7

Se cortan cuatro triángulos rectángulos isósceles congruentes de las $ 4 $ esquinas de un cuadrado de lado $ 20 $ unidades. La longitud de un cateto de los triángulos es $ 4 $ unidades. ¿Cuál es el área del octágono restante?

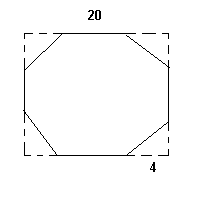
Problema 7

Solución:

Área del cuadrado: $ 20 \times 20 = 400 $.

Área de un triángulo: $ \dfrac{1}{2} \times 4 \times 4 = 8 $.

Área total de triángulos: $ 4 \times 8 = 32 $.

Área del octágono: $ 400 - 32 = 368 $ unidades cuadradas.

Problema 8

Un automóvil viaja a 75 kilómetros por hora. ¿Cuántos metros recorre el automóvil en un minuto?

Solución:

75 km/h = $ 75 \times 1000 = 75000 $ m/h.

1 hora = 60 minutos.

Metros por minuto: $ \dfrac{75000}{60} = 1250 $ m/min.

Problema 9

Linda gastó 3/4 de sus ahorros en muebles y el resto en un televisor. Si el televisor le costó $200, ¿cuáles eran sus ahorros originales?

Solución:

Sea $ S $ los ahorros originales.

Gastó $ \dfrac{3}{4}S $ en muebles, resto $ \dfrac{1}{4}S $ en TV = $200.

Ecuación: $ \dfrac{1}{4}S = 200 \Rightarrow S = 800 $.

Ahorros originales: $800.

Problema 10

La altura del agua en un contenedor cilíndrico de radio $ r $ es $ 15 $ cm. ¿Cuál será la altura de esta cantidad de agua si se vierte en un contenedor cilíndrico de radio $2 r $?

Solución:

Volumen original: $ V = \pi r^2 \times 15 $.

Nuevo radio: $ 2r $. Nueva altura: $ h_2 $.

Volumen constante: $ \pi r^2 \times 15 = \pi (2r)^2 \times h_2 $.

Simplificando: $ 15 = 4 h_2 \Rightarrow h_2 = 3.75 $ cm.

Problema 11

Stuart compró un suéter con un descuento del 30% sobre el precio original y luego otro $ 25\% $ sobre el precio descontado. Si el precio original era $ \$ 30 $, ¿cuál fue el precio final?

Solución:

Precio original: $30.

Primer descuento (30%): $30 - $9 = $21.

Segundo descuento (25% sobre $21): $21 - $5.25 = $15.75.

Precio final: $15.75.

Problema 12

John compró una camisa con un descuento del 25% sobre el precio original y luego otro $ 25 \% $ sobre el precio descontado. Si el precio final fue $ \$ 16 $, ¿cuál era el precio antes del primer descuento?

Solución:

Sea $ P $ el precio original.

Después del primer descuento: $ 0.75P $.

Después del segundo descuento: $ 0.75P - 0.25(0.75P) = 0.5625P $.

Igualando a $16: $ 0.5625P = 16 $.

Resolviendo: $ P = \dfrac{16}{0.5625} \approx 28.44 $.

Precio original: aproximadamente $28.44.

Problema 13

¿Cuántas pulgadas hay en 2000 milímetros? (redondea a la centésima más cercana).

Solución:

1 mm = 0.0393701 pulgadas.

2000 mm = $ 2000 \times 0.0393701 = 78.74 $ pulgadas.

Problema 14

El patio rectangular en la escuela de Tim es tres veces más largo que ancho. El área del patio es $ 75 $ metros cuadrados. ¿Cuál es el perímetro del patio?

Solución:

Ancho = $ w $, Largo = $ 3w $.

Área: $ 3w \times w = 75 \Rightarrow 3w^2 = 75 \Rightarrow w^2 = 25 \Rightarrow w = 5 $.

Largo: $ 3 \times 5 = 15 $.

Perímetro: $ 2(15 + 5) = 40 $ metros.

Problema 15

John tenía un stock de 1200 libros en su librería. Vendió 75 el lunes, 50 el martes, 64 el miércoles, 78 el jueves y 135 el viernes. ¿Qué porcentaje de libros no se vendió?

Solución:

Total vendido: $ 75 + 50 + 64 + 78 + 135 = 402 $.

No vendidos: $ 1200 - 402 = 798 $.

Porcentaje no vendido: $ \dfrac{798}{1200} \times 100 = 66.5\% $.

Problema 16

N es uno de los números a continuación. N es tal que al multiplicarlo por 0.75 da 1. ¿Qué número es igual a N?

A) $ 1 \dfrac{1}{2} $

B) $ 1 \dfrac{1}{3} $

C) $ \dfrac{5}{3} $

D) $ \dfrac{3}{2} $

Solución:

Ecuación: $ N \times 0.75 = 1 $.

Resolviendo: $ N = \dfrac{1}{0.75} = \dfrac{4}{3} $.

Opción B: $ 1 \dfrac{1}{3} = \dfrac{4}{3} $.

Respuesta: B.

Problema 17

En 2008, la población mundial era de aproximadamente 6,760,000,000. Escribe la población mundial de 2008 en notación científica.

Solución:

6,760,000,000 = $ 6.76 \times 10^9 $.

Problemas de Matemáticas de 7º Grado con Soluciones

Problema 1

Problema 2

Problema 3

Problema 4

Problema 5

Problema 6

Problema 7

Problema 8

Problema 9

Problema 10

Problema 11

Problema 12

Problema 13

Problema 14

Problema 15

Problema 16

Problema 17

Más Referencias y Enlaces