1 - Numbers
\( \pi \) is NOT a rational number.
The value of the digit 5 in the number 34.6597 is \[ 0.05 \quad \text{or} \quad \dfrac{5}{100} \] \( \) \( \)\( \) \( \require{cancel} \) \( \require{bbox} \)
2 - Sequences
We notice that as we go from one term to the next, we add \( 3 \); hence the next term is equal to : \( 12 + 3 = 15 \)
a) The first five terms of the sequence starting with \( n = 1 \) are obtained by substituting \( n \) by \( 1, 2, 3, 4, 5 \) in the expression \( 2 n + 1 \) :
For \( n = \color{red}1 \) , \( 2 n + 1 = 2( \color{red}1) + 1 = 3 \)
For \( n = \color{red}2 \) , \( 2 n + 1 = 2(\color{red}2) + 1 = 5 \)
For \( n = \color{red}3 \) , \( 2 n + 1 = 2(\color{red}3) + 1 = 7 \)
For \( n = \color{red}4 \) , \( 2 n + 1 = 2(\color{red}4) + 1 = 9 \)
For \( n = \color{red}5 \) , \( 2 n + 1 = 2(\color{red}5) + 1 = 11 \)
b) Going from one term to the next, we add \( 2 \) and hence it is an arithmetic sequence with common difference equal to \( 2 \).
a) The first five terms of the sequence starting with \( n = 1 \) are obtained by substituting \( n \) by \( 1, 2, 3, 4, 5 \) in the expression \( 3 \times 2^{n-1} \) :
For \( n = \color{red}1 \) , \( 3 \times 2^{n-1} = 3 \times 2^{\color{red}1-1} = 3 \times 2^{0} = 3 \)
For \( n = \color{red}2 \) , \( 3 \times 2^{n-1} = 3 \times 2^{\color{red}2-1} = 3 \times 2^{1} = 6 \)
For \( n = \color{red}3 \) , \( 3 \times 2^{n-1} = 3 \times 2^{\color{red}3-1} = 3 \times 2^{2} = 12 \)
For \( n = \color{red}4 \) , \( 3 \times 2^{n-1} = 3 \times 2^{\color{red}4-1} = 3 \times 2^{3} = 24 \)
For \( n = \color{red}5 \) , \( 3 \times 2^{n-1} = 3 \times 2^{\color{red}5-1} = 3 \times 2^{4} = 48 \)
b) Going from one term to the next, we multiply by \( 2 \) and hence it is a geometric sequence with common ratio equal to \( 2 \).
3 - Sets
a) The intersection of two sets is the set of all elements common to both sets. Hence
\( S_1 \cap S_2 = \{ 2, 9, 12 \} \)
b) The union of two sets is the set of all elements in the two sets ( without repetition ). Hence
\( S_1 \cup S_2 = \{ 0, 2, 9, 10, 11, 12 \}\)
Any real number is either rational or irrational but not both, hence
\( Q \cap P = \text{Empty Set} \)
The set of all real numbers is the union of the rational and irrational numbers, hence
\( Q \cup P = R \)
b) and d) are true.
4 - Factors, Multiples and Divisibility of Numbers
a) \( \; 345 = 3 \times 5 \times 23 \)
b) \( \; 150 = 2 \times 3 \times 5 \times 5 \)
c) \( \; 210 = 2 \times 3 \times 5 \times 7 \)
A number is divisible by \( 3 \) if the sum of its digits is divisible by \( 3 \).
a)
add all digits in the given number \( 101899 \): \[ 1+0+1+8+9+9 = 28 \].
The result \( 28 \) is not divisible by \( 3 \) and therefore the given number \( 101899 \) is not divisible by \( 3 \)
b)
add all digits in the given number \( 900234 \): \[ 9+0+0+2+3+4 = 18 \]
The result \( 18 \) is divisible by \( 3 \) and therefore the given number \( 900234 \) is divisible by \( 3 \)
c)
add all digits in the given number \( 134567280 \): \[ 1+3+4+5+6+7+2+8+0 = 36 \]
\( 36 \) is divisible by \( 3 \) and therefore the given number \( 134567280 \) is divisible by \( 3 \)
A number is divisible by \( 4 \) if its two digits on the right form a number that is divisible by \( 3 \).
a)
The two digits on the right of the given number \( 1890\color{red}{01} \) are \( 01 \) which form a number that is not divisible by \( 4 \) and therefore \( 189001 \) is not divisible by \( 4 \).
b)
The two digits on the right of the given number \( 10056\color{red}{12} \) are \( 12 \) which form a number that is divisible by \( 4 \) and therefore \( 1005612 \) is divisible by \( 4 \).
c)
The last two digits in the given number \( 10034560\color{red}{24} \) are \( 24 \) which form a number that is divisible by \( 4 \) and therefore \( 1003456024 \) is divisible by \( 4 \).
For a number to be divisible by \( 6 \), it has to be divisible by \( 2 \) and by \( 3 \)
a)
\( 234 \) is divisible by \( 2 \) since its last digit on the right is \( 4 \) . It is also divisible by \( 3 \) since the sum of its digits \( 2+3+4 = 9 \) is divisible by \( 3 \). Therefore \( 234 \) is divisible by \( 6 \)
b)
\( 12345 \) is not divisible by \( 6 \) because it is not divisible by \( 2 \)
c)
\( 12114290910 \) is divisible by \( 2 \) since its last digit on the right is \( 0 \). The sum of its digits \( 1+2+1+1+4+2+9+0+9+1+0 = 30 \) is divisible by \( 3 \) and therefore the given number \( 12114290910 \) is also divisible by \( 3 \). Since the given number is divisible by \( 2 \) and by \( 3 \), it is divisible by \( 6 \).
5 - Fractions and Mixed Numbers
Start with the fraction in reduced terms and multiply by a factor in order to obtain the second fraction if possible.
a) Multiply numerator and denominator of the fraction \( \displaystyle \frac{7}{3} \) by \( 5 \) and simplify
\( \displaystyle \frac{7 \times 5 }{3 \times 5 } = \frac{35}{15} \)
We obtain a fraction with the same denominator but not the same numerator as the given fraction \( \displaystyle \frac{10}{15} \) hence the two fractions are NOT equivalent.
b) Multiply numerator and denominator of the fraction \( \displaystyle \frac{2}{3} \) by \( 4 \) and simplify
\( \displaystyle \frac{2 \times 4}{3 \times 4 } = \frac {8}{12}\)
We obtain a fraction with the same denominator and the same numerator as the given fraction \( \displaystyle \frac{8}{12} \) hence the two fractions are equivalent.
c) Multiply numerator and denominator of the fraction \( \displaystyle \frac{7}{12} \) by \( 3 \) and simplify
\( \displaystyle \frac{7 \times 3 }{12 \times 3} = \frac{21}{36} \)
We obtain a fraction with the same denominator and the same numerator as the given fraction \( \displaystyle \frac{21}{36} \) hence the two fractions are equivalent.
a) Rewrite the three fractions to the lowest common denominator which is the lowest common multiple (LCM) of the denominators \( 5, 10 \) and \( 15 \). LCM of \( 5, 10 , 15 \) = \( 30 \)
Hence
\( \displaystyle \frac{2}{5} + \frac{3}{10} - \frac{1}{15} \\~\\ \quad \quad = \frac{2 \times 6 }{5 \times 6} + \frac{3 \times 3}{10 \times 3} - \frac{1 \times 2}{15 \times 2} \\~\\ \quad \quad = \frac{12 }{30} + \frac{9}{30} - \frac{2}{30} \\~\\ \quad \quad = \frac{19}{30} \)
b) Multiply denominators together and numerators together
\( \displaystyle \frac{7}{16} \times \frac{4}{14} = \frac{7 \times 4}{16 \times 14} \)
Factor the terms \( 16 = 4 \times 4 \) and \( 14 = 2 \times 7 \) in the denominator
\( \displaystyle = \frac{7 \times 4}{(4 \times 4) \times (2 \times 7)} \)
Cancel common factors and simplify
\( \quad \quad \displaystyle = \frac{\cancel{\color{blue}{7}} \times \cancel{\color{red}{4}}}{(\cancel{\color{red}{4}}\times 4) \times (2 \times \cancel{\color{blue}{7}})} = \frac{1}{8} \)
c) Rewrite the division of the fractions as a multiplication by the reciprocal; hence
\( \displaystyle \frac{11}{2} \div 4 = \frac{11}{2} \times \frac{1}{4} \)
Simplify
\( \quad \quad = \frac{11}{8} \)
d) Group the whole parts together and the fractions together
\( \displaystyle 4 \frac{3}{4} - 1 \frac{1}{2} + 1 \frac{1}{8} = (4-1+1) + (\frac{3}{4} - \frac{1}{2} + \frac{1}{8} ) \)
Simplify
\( \quad \quad = 4 \frac{3}{8} \)
e) Convert the expressions \( \displaystyle 1 \frac{3}{4} \) and \( 3 + \frac{1}{3} \) into fractions.
\( \displaystyle 1 \frac{3}{4} = \frac{7}{4} \) and \( 3 + \frac{1}{3} = \frac{10}{3} \)
Rewrite the given expression using fractions only
\( \displaystyle 1 \frac{3}{4} \div \left(3 + \frac{1}{3} \right) = \frac{7}{4} \div \frac{10}{3} \)
Rewrite the division as a multiplication by the reciprocal
\( \quad \quad = \frac{7}{4} \times \frac{3}{10} \)
Simplify
\( \quad \quad = \frac{21}{40} \)
a) \( 0.2 \div 0.6 = \frac{2}{6} = \frac{1}{3} \)
b) \( 1 \div 0.4 = \frac{10}{4} \)
It is an improper fraction and may therefore be written as a mixed number
\( \quad \quad = \frac{8+2}{4} = \frac{8}{4} + \frac{2}{4} = 2 \frac{1}{2} \)
Dalia spends "\( \frac{1}{4} \) of her salary" on food and beverages
\( \frac{1}{5} \) of "\( \frac{1}{4} \) of her salary" is spent on soft drinks
\( \frac{1}{6} \) of "\( \frac{1}{4} \) of her salary" is spent on cookies
Total spent on soft drinks and cookies : \( \frac{1}{5} \) of "\( \frac{1}{4} \) of her salary" plus \( \frac{1}{6} \) of "\( \frac{1}{4} \) of her salary"
which may be written as
\( \frac{1}{5} \times \frac{1}{4} + \frac{1}{6} \times \frac{1}{4} = \frac{1}{4} ( \frac{1}{5} + \frac{1}{6}) = \frac{11}{120} \)
Dalia spends \( \frac{11}{120} \) of her salary on soft drinks and cookies.
Ben spends : \( \frac{3}{4} \times 10 = 7.5 \) hours on homework during weekdays
Linda spends: \( \frac{5}{4} \times 10 = 12.5 \) hours on homework during weekdays
Using mixed numbers, a liter and a half of juice is written as : \( 1\frac{1}{2} \)
Using fractions, one sixth of a liter is written as : \( \frac{1}{6} \)
Number of glasses that can be filled = \( 1\frac{1}{2} \div \frac{1}{6} = 9 \)
6 - Exponents and Scientific Notation
a) \( (-2)^3 - 5^3 + (-3)^4 \\~\\ \quad \quad = - 8 - 125 + 81 \\~\\ \quad \quad = - 52\)
b) \( \quad (-1)^{-3} - 5^0 + \frac{4^2}{(-2)^4} \\~\\ \quad \quad = \frac{1}{(-1)^3} - 1 + \frac{16}{16} \\~\\ \quad \quad = \frac{1}{-1} -1 +1 = -1 \)
c) \( \quad \left( \frac{3}{4} \right)^2 + \left( \frac{4}{3} \right)^{-2} \\~\\ \quad \quad = \frac{3^2}{4^2} + \frac{4^{-2}}{3^{-2}} \\~\\ \quad \quad = \frac{9}{16} + \frac{3^2}{4^2} \\~\\ \quad \quad = \frac{9}{8}\)
a) \( 10000 = 10^4\)
b) \( 0.0000001 = 10^{-7}\)
c) \( \frac{1}{100000} = \frac{1}{10^5} = 10^{-5}\)
a) \( 12.4 \times 10^3 = 1.24 \times 10^4\)
b) \( 0.0023 \times 10^{-2} = 2.3 \times 10^{-5} \)
c) \( \frac{12}{100000} = \frac{12}{10^5} = 12 \times 10^{-5} = 1.2 \times 10^{-4}\)
7 - Roots
a) \( \sqrt{16} = 4 \) because \( 4^2 = 16 \)
b) \( \quad \sqrt{9} = 3 \) because \( 3^2 = 9 \)
b) \( \quad \sqrt[3]{8} = 3 \) because \( 3^3 = 8 \)
a) \( \sqrt{3 \times 25} = \sqrt{3 } \times \sqrt{ 25} = 5 \sqrt{3 } \)
b) \( \quad \sqrt{36 \times 5} = \sqrt{36} \times \sqrt{ 5} = 6 \sqrt{ 5} \)
b) \( \quad \sqrt[3]{8 \times 7} = \sqrt[3]{8 } \times \sqrt[3]{7} = 2 \sqrt[3]{7} \)
8 - Proportionality and Related Problems
a) Use a point on the graph. For example, when \( t = 1 \) , \( d = 4 \)
Substitute \( t \) by \( 1 \)and \( d \) by \( 4 \) in the equation \( d = k \times t\) to obtain
\( 4 = k \times 1 \)
Simplify to obtain
\( k = 4 \)
Hence the relationship between the distance \( d \) and the \( time \) is given by
\[ d = 4 \times t\] , with \( d \) in km and \( t \) in hours.
b) Find time it takes Leila to walk d = 10 km by solving the equation
\( 10 = 4 t \)
Solve for \( t \)
\( t = 10 \div 4 = 2.5 \) hours
\( 2.5 \) hours may also be written as \( 2:30 \)
She is 10 km away from her starting point at : \( 8 + 2:30 = 10:30 \)

A column that contains the ratio \( y / x \) was added and it shows that \( y / x \) is constant and equal to \( 3 \). Hence
\( y \) is proportional to \( x \)?

a)
Since \( y / x = 3 \), we can write \( y = 3 x \)
Hence
\( k = 3 \)
b)
\( y = 3 \times 10.2 = 30.6 \)
a) Form the given information, we can write three points of the form \( (V , t) \) and they are: \( (2,10) \) , \( (4,20) \) and \( (6,30) \) which are plotted below.

b) The three points are located in the same line and therefore there is a proportionality relationship between \( V \) and \( t \).
c) The constant of proportionality \( k \) is defined in the equation \( V = k \; t \). Hence
\[ k = V \div t \]
Use any of the three points above, \( k \) is found as follows
\( k = V \div t = 10 \div 2 = 5 \)
or \( k = V \div t = 20 \div 4 = 5 \)
or \( k = V \div t = 30 \div 6 = 5 \)
Hence
\( V = 5 t \)
d) Since we have the relationship between \( V = k \; t \) and \( V = 100 \), we substitute \( V \) by \( 100 \) in the equation \( V = 5 t \).
\( 100 = 5 t \)
Solve the above equation for \( t \)
\( t = 100 \div 5 = 20 \) minutes are needed to fill a tank of 100 Liters.
9 - Percent and Related Problems
Price after increase = \( 120 \) + increase = \( 120 \) + \( 12\% \) of \( 120 \)
which is written mathematically as
Price after increase = \( 120 + 12\% \times 120 = 120 + \frac{12}{100} \times 120 \\~\\ = 120 + 14.4 \\~\\ = \$134.40 \)
The percent of Jimmy's salary spent on bills = \( 15\% \) of \( 50\% \) of his salary
which is mathematically written as
\( \frac{15}{100} \times \frac{50}{100} \\~\\ = \frac{15 \times 50}{100 \times 100} \\~\\ = \frac{750}{10000} \\~\\ = \frac{7.5}{100} \\~\\ = 7.5\% \)
Cost after tax = \( 40 + 15\% \text{ of } 40 = 40 + \frac{15}{100} \times 40 = \$46\)
Cost after tip = \( 46 + \frac{5}{100} \times 46 = \$48.30 \)
Kamelea's spending \( = \$400 + \$1200 + \$200 + \$1200 + \$600 = \$3600 \)
Savings = Salary - spending \( = \$5000 - \$3600 = \$1400 \)
Kamelea's savings in percent of salary = \( \frac{1400}{5000} = 0.28 = 28 \% \)
Let \( x \) be the unknown number. We are given that
\( 10\% \) of \( \frac{1}{3} \) of \(x \) = 3
which is written mathematically as
\( \frac{10}{100} \times \frac{1}{3} \times x = 3 \)
The above equation may be written as
\( \frac{10 x}{300} = 3 \)
Multiply both sides of the equation by \( 300 \)
\( \frac{10 x}{300} \times 300 = 3 \times 300 \)
Simplify
\( 10 x = 900 \)
Solve for \( x \)
\( x = 900 \div 10 = 90 \)
Percentage increase of gas in the US = \( \frac{4 - 3}{3} = 0.33333 = 33.33\% \)
Percentage increase of gas in the France = \( \frac{2 - 1.5}{1.5} = 0.33333 = 33.33\% \)
The US and France saw the same percentage of gas increase in that year.
10 - Convert Units of Measurement
Divide both sides of the equality \( \quad 1 \text{ m} = 3.28084 \text{ ft} \quad \) by \( \quad 3.28084 \text{ ft} \quad \)
\( \frac{1 \text{ m}}{3.28084 \text{ ft}} = \frac{3.28084 \text{ ft}}{3.28084 \text{ ft}} \)
Simplify to obtain
\( \frac{1 \text{ m}}{3.28084 \text{ ft}} = 1 \)
We now write the given length \( 10.5 \text{ ft} \) as
\( 10.5 \text{ ft} = 10.5 \text{ ft} \times 1 \)
Substitute \( 1 \) by \( \frac{1 \text{ m}}{3.28084 \text{ ft}} \). Hence
\( 10.5 \text{ ft} = 10.5 \text{ ft} \times \frac{1 \text{ m}}{3.28084 \text{ ft}} \)
Cancel \( \text{ ft} \)
\( 10.5 \text{ ft} = 10.5 \cancel{\text{ ft}} \times \frac{1 \text{ m}}{3.28084 \cancel{\text{ ft}}} \)
Calculate to obtain
\( 10.5 \text{ ft} = 10.5 \cancel{\text{ ft}} \times \frac{1 \text{ m}}{3.28084 \cancel{\text{ ft}}} = 3.20039 \text{ m}\)
\( 1.3 \text{ km} = 1.3 \times 1093.61 \text{ yd} = 1421.69 \text{ yd} \)
Square both sides of the given equality \( 1 \; m = 1.09361 \; yd \) to obtain
\( (1 \; m) \times (1 \; m) = (1.09361 \; yd) \times (1.09361 \; yd) \)
Simplify
\( 1 \; m^2 = 1.19598 \; yd^2 \)
\( 1.2 \; m^2 = 1.2 \times 1.19598 \; yd^2 = 1.435176 \; yd^2\)
\( 1 \; km = 1000 \; m \) and \( 1 \; hr = 3600 \;sec \)
Hence
\( 100 \; km / hr = \frac{100 \; km}{1 hr} = \frac{100 \times 1000 \; m }{1 \times 3600 \; sec}\)
Simplify
\( 100 \; km / hr = 27.77777 \; m/sec \)
11 - Evaluate Expressions
Substitute \( x \) by \( 1 \) in the given expression
\( \; \frac{1}{x+2} - \frac{1}{x-2} = \frac{1}{(1)+2} - \frac{1}{(1)-2}\; \)
Evaluate
\( = \frac{1}{3} - \frac{1}{-1} = \frac{1}{3} + 1 = 1 \frac{1}{3} \; \)
Substitute \( x \) by \( -5 \) in the given expression
\( \; | \frac{-x+1}{-6} | + x^2 - 1 = | \frac{-(-5)+1}{-6} | + (-5)^2 - 1 \; \)
Evaluate
\( = | \frac{5+1}{-6} | + 25 - 1 = | -1 | + 25 - 1 \\~\\ = 1 + 25 - 1 = 25 \)
Substitute \( a\) and \( b \) by \( 2 \) and \( -2 \) respectively in the given expression
\( \; 2^a - \sqrt{b^2} = 2^{(2)} - \sqrt{(-2)^2}\; \)
Evaluate
\( = 4 - \sqrt{4} = 4 - 2 = 2 \)
12 - Algebra
Review
The distributive property in algebra may be used to expand as follows
\[ a (x + y ) = \color{red}a \times x + \color{red}a \times y \]
The distributive property may also be used in reverse to factor as follows
\[ \color{red}a \times x + \color{red}a \times y = \color{red}a (x + y ) \]
a)
Use the distributive property on the expression \( 3 (x + 2) \)
\( 3 (x + 2) + x - 12 = 3 x + 3\times 2 + x - 12 \\~\\ \qquad = 3 x + 6 + x - 12 \)
Group like terms
\( = (3 x + x) + (6 -12) \)
Simplify
\( = 4 x - 6 \)
b)
Use the distributive property on the expression \( \displaystyle \frac{1}{5}( 15 x + 20) \)
\( \displaystyle \frac{1}{5}( 15 x + 20) + 2x + 4 = \frac{1}{5} \times 15 x + \frac{1}{5} \times 20 + 2x + 4 \)
Simplify using \( \frac{1}{5} \times 15 x = \frac{15}{5} x = 3 x \) and \( \frac{1}{5} \times 20 = \frac{20}{5} = 4 \)
\( = 3 x + 4 + 2x + 4 \)
Group like terms
\( = (3x + 2x) + ( 4 + 4 ) \)
Simplify
\( = 5x + 8 \)
c)
Use the distributive property on the expression \( 0.2 ( 5 x + 10) \)
\( 0.2 ( 5 x + 10) + 3x - 4 = 0.2 \times 5 x + 0.2 \times 10 + 3x - 4 \)
Simplify
\( = x + 2 + 3x - 4 \\~\\ \qquad = (x+3x) + (2-4) \\~\\ \qquad = 4x - 2 \)
Simplify the expressions
a)
\( 2x \times 3 x = (2 \times 3) \times ( x \times x ) = 6 x^2\)
b)
\( \displaystyle \frac{1}{2}x \times \frac{4}{5} x = (\frac{1}{2} \times \frac{4}{5} ) \times (x \times x) = \frac{2}{5} x^2 \)
c)
\( 3x^2 \times 5 x^3 = (3 \times 5) \times (x^2 \times x^3) = 15 x^{2+3} = 15 x^5 \)
a)
The greatest common factor of the coefficients \( 21 \) and \( 7 \) is equal to \( 7 \), hence
\( 21 x + 7 = \color{red}7 \times 3 x + \color{red}7 \times 1\)
Use the distributive property in reverse to factor \( 7 \) out.
\( = 7 ( 3x + 1 ) \)
b)
The greatest common factor of the coefficients \( 24 \) and \( 20 \) is equal to \( 4 \), hence
\( 24 - 20 x = \color{red}4 \times 6 - \color{red}4 \times 5x \)
Use the distributive property in reverse to factor \( 4 \) out.
\( = 4 (6 - 5x) \)
c)
The greatest common factor of the coefficients \( 8 \), \( 4 \) and \( 32 \) is equal to \( 4 \), hence.
\( 8 b - 4 a + 32 = \color{red}4 \times 2 b - \color{red}4 \times a + \color{red}4 \times 8\)
Use the distributive property in reverse to factor the \( 4 \) out
\( = 4 (2b - a + 8) \)
13 - Equation with One Variable and Related Problems
a)
Given the equation \( 3(x - 2 ) = 3 \)
Expand the expression \( 3(x - 2 ) \) using the distributive property
\( 3 x - 6 = 3 \)
Add \( 6 \) to both sides
\( 3 x - 6 + 6 = 3 + 6 \)
Simplify
\( 3 x = 9 \)
Divide both sides by \( 3 \)
\( 3 x \div 3 = 9 \div 3\)
Simplify and solve for \( x \).
\( x = 3 \)
b)
Given the equation \( 2(9 - x) = - (x + 5) \)
Expand the parentheses in both sides of the equation using the distributive property
\( 18 - 2 x = - x - 5 \)
Add \( 2x \) to both sides of the equation and simplify
\( 18 - 2 x + 2x = - x - 5 + 2x \)
\( 18 = x - 5 \)
Add \( 5 \) to both sides and simplify
\( x = 23 \)
c)
Given the equation \( \displaystyle \frac{x+1}{3} = 6 \)
Multiply both sides by the denominator \( 3 \)
\( \displaystyle \frac{x+1}{3} \times 3 = 6 \times 3\)
Simplify
\( x+1 = 18 \)
Solve for \( x \)
\(x = 17 \)
d)
Given the equation \( 4 \left(x + \displaystyle \frac{1}{4} \right) = -15\)
Expand the parentheses on the left side of the equation using the distributive property
\( 4 x + 4 \times \frac{1}{4} = -15\)
Simplify
\( 4 x + 1 = -15\)
Solve for \( x \)
\( 4 x + 1 - 1 = -15 - 1\)
\( 4 x = -16\)
\( x = - 4 \)
e)
Given the equation \( x - \displaystyle \frac{x}{2} = 3 \)
Multiply all terms by the denominator \( 2 \).
\( x \times 2 - \displaystyle \frac{x}{2} \times 2 = 3 \times 2 \)
Simplify and solve for \( x \).
\( 2 x - x = 6 \)
\( x = 6 \)
Given

a)
Length of outer perimeter: \( L = 12 + x + x = 12 + 2x\)
Width of outer perimeter: \( W = 8 + x + x = 8 + 2x \)
Outer perimeter \( = 2 \times L + 2 \times W = 2 (12 + 2x) + 2(8 + 2x) \)
Expand and group like terms
Outer perimeter \( = 24 + 4x + 16 + 4x = 40 + 8x \)
Perimeter of the garden (in white) \( = 2 \times 12 + 2 \times 8 = 40 \)
Given that "outer perimeter is equal to twice the perimeter of the garden", we can write the equation
\( 40 + 8x = 2 \times 40 \)
b)
Simplify the right side of the equation obtained in a)
\( 40 + 8x = 80 \)
Solve for \( x \)
\( 8x = 40 \)
\( x = 5 \; \text{ m} \)
c) \( L = 12 + 2x = 12 + 2 \times 5 = 22 \; \text{ m} \)
\( W = 8 + 2x = 8 + 2 \times 5 = 18 \; \text{ m} \)
d)
Area of garden and path = \( = L \times W = 22 \times 18 = 396 \; m^2\)
e) Area of garden = \( 12 \times 8 = 96 \; m^2\)
f) The area of the path = Area of garden and path - Area of garden \( = 396 - 96 = 300 \; m^2\).
"10 is subtracted from twice a number" is written as : \( 2x - 10 \)
"the result is multiplied by half" is written as : \( \frac{1}{2} (2x - 10) \)
"the answer is 5" is written as : \( \frac{1}{2} (2x - 10) = 5\)
Multiply both sides of the equation and simplify
\( \frac{1}{2} (2x - 10) \times 2 = 5 \times 2\)
\( 2x - 10 = 10 \)
The original number is equal to \( 10 \)
14 - Inequality with One Variable
a)
Given the inequality \( x+2 \lt 4 \)
Subtract \( 2 \) from both sides of the inequality and simplify
\( x+2 -2 \lt 4 -2 \)
\( x \lt 2 \)
b)
Given the inequality \( 2(x + 3)\ge 2 \) Expand the parentheses on the left side of the inequality using the distributive property and simplify
\( 2 \times x + 2 \times 3 \ge 2 \)
\( 2 x + 6 \ge 2 \)
Subtract \( 6 \) from both sides of the inequality and simplify
\( 2 x + 6 - 6 \ge 2 - 6 \)
\( 2 x \ge - 4 \)
Divide both sides of the inequality by \( 2 \) and simplify
\( \frac{2 x}{2} \ge \frac{ - 4}{2} \)
\( x \ge -2 \)
c) Given the inequality \( -3x+2 \le 11 \)
Subtract \( 2 \) from both sides of the inequality and simplify
\( -3x+2 -2 \le 11 - 2 \)
\( -3x \le 9 \)
Divide both sides of the inequality by \( -3 \) and change the symbol of the inequality because \(-3 \) is negative.
\( \frac{-3x}{-3} \color{red}{ \ge } \frac{9}{-3} \)
Simplify
\( x \ge - 3 \)
d) Given the inequality \( \frac{4x+1}{2} \ge x+3 \)
Multiply both sides of the inequality by the denominator \( 2 \)
\( \frac{4x+1}{2} \times 2 \ge (x+3) \times 2 \)
Simplify
\( 4x+1 \ge 2x + 6 \)
Subtract \( 1 \) from both sides of the inequality and simplify
\( 4x+1 - 1\ge 2x + 6 - 1 \)
\( 4x \ge 2x + 5 \)
Subtract \( 2x \) from both sides of the inequality and simplify
\( 4x - 2x \ge 2x + 5 - 2x \)
\( 2x \ge 5 \)
Divide both sides of the inequality by \( 2 \) and simplify
\( x \ge 5/2 \)
15 - Functions
A function is a relation between two sets such that to each input there corresponds one output only.
a)
The relation \( \{ (1,2) , (3,4) , (5,7) , (5,9) \} \) is NOT a function because to the input \( 5 \) correspond two outputs: \(7 \) and \( 9 \).
b)
The relation \( \{ (-1,-2) , (3,4) , (5,7) , (7,9) \} \) is a function because to each input corresponds one output only
c)
The relation \( \{ (3,3) , (9,4) , (5,7) , (9,0) \} \) is NOT a function because to the input \( 9 \) correspond two outputs: \( 4 \) and \( 0 \).
Graph (3) is a line and is therefore the graph of a linear function.

a)
for \( x = 0 \) , \( y = 2 x + 1 = 2(0) + 1 = 1\)
for \( x = 1 \) , \( y = 2 x + 1 = 2(1) + 1 = 3\)
b) The results in part a) may be represented by ordered pairs \( (x , y) \) as \( (0 , 1) \) and \( (1 , 3) \)
The given function \( y = 2 x + 1 \) is a linear function and its graph is a line and therefore the two ordered pairs obtained above may be used to graph the function as shown below.

a) The function corresponding to graph (1) has a higher rate of change because it increases faster as \( x \) increases.
b)

Points on Graph (1) : \( (0,1) \) , \( (3,7) \) ; there are many other points
Points on Graph (2) : \( (0,3) \) , \( (8,8) \) ; there are many other points
c)
Rate of change of Graph (1) : \( r_1 = \frac{\text{Change in y} }{\text{Change in x}} = \frac{7-1}{3 - 0} = 2 \)
Rate of change of Graph (2) : \( r_2 = \frac{\text{Change in y} }{\text{Change in x}} = \frac{8-3}{8 - 0} = 5/8 \)
d)
Calculations show that the rate of change of (1) is higher than the rate of change of graph (2) which confirm the answer to part a) above.
16 - Two-Dimensional Figures
Let \( h \) be the hypotenuse of the triangle and apply the Pythagorean theorem to write
\( h^2 = 6^2 + 8^2 \)
Solve for \( h \) by taking the square root of both sides of the above equation.
\( h = \sqrt {6^2 + 8^2} \\~\\ \qquad = \sqrt {36 + 64} \\~\\ \qquad = \sqrt{100} \\~\\ \qquad = 10 \text{ cm}\)
Note that \( \angle AOC = \angle AOB + \angle BOC \)
Substitute the known angles by their sizes.
\( 79^{\circ} = 31^{\circ} + \angle BOC \)
Hence
\( \angle BOC = 79^{\circ} - 31^{\circ} = 48^{\circ} \)
Note that angles \( \angle BOC \) and \( \angle EOF \) are vertical and therefore have equal sizes. Hence
\( \angle EOF = 48^{\circ} \)

A square has 4 lines of symmetry as shown below.

Angles \( m \angle 1 \) and \( m \angle 2 \) are supplementary and therefore their sum is equal to \( 180^{\circ} \). Hence
\( 40^{\circ} + m \angle 2 = 180^{\circ} \)
Solve for \( m \angle 2 \)
\( m \angle 2 = 180^{\circ} - 40^{\circ} = 140^{\circ}\)
\( m \angle 1 \) and \( m \angle 3 \) are vertical and therefore have equal measure, hence
\( m \angle 3 = m \angle 1 = 40^{\circ} \)
\( m \angle 2 \) and \( m \angle 4 \) are vertical and therefore have equal measure, hence
\( m \angle 4 = m \angle 2 = 140^{\circ} \)
\( m \angle 1 \) and \( m \angle 5 \) are corresponding angles and therefore have equal measure, hence
\( m \angle 5 = m \angle 1 = 40^{\circ}\)
\( m \angle 2 \) and \( m \angle 6 \) are corresponding angles and therefore have equal measure, hence
\( m \angle 6 = m \angle 2 = 140^{\circ}\)
\( m \angle 4 \) and \( m \angle 8 \) are corresponding angles and therefore have equal measure, hence
\( m \angle 8 = m \angle 4 = 140^{\circ}\)
\( m \angle 3 \) and \( m \angle 7 \) are corresponding angles and therefore have equal measure, hence
\( m \angle 7 = m \angle 3 = 40^{\circ}\)

17 - Perimeter and Area of Planar Figures
Radius: \( r = \text{Diameter} \div 2 = 20 \div 2 = 10 \text{ cm} \)
\( \text{Area} = \pi \times r^2 = 3.14 \times 10^2 = 3.14 \times 100 = 314 \; cm^2 \)
The area \( A \) of a right triangle with legs \( a \) and \( b \) is given by
\( A = \frac{1}{2} \times a \times b \)
We are given the size of one leg \( a = 16 \) and we need to find the size of the second leg \(b\).
Use the Pythagorean theorem to find the second leg \( b\) of the right triangle
\( b^2 + 16^2 = 20^2 \)
Hence
\( b^2 = 20^2 - 16^2 = 144\)
\( b = \sqrt {144} = 12 \; cm \)
Area of the right triangle is equal to: \( \frac{1}{2} \times 16 \times 12 = 96 \; cm^2 \)
Because of the symmetry, we calculate the area of the lower part of the arrow which is a trapezoid whose \( A \) area is given by

\( A = \frac{1}{2} (\overline{FG}+ \overline{ED}) \times \overline{HE} \)
\( \overline{FG} = 12 + 16 - 4 = 24 \)
\( \overline{ED} = 16 \)
Since ABDE is a square, we have \( \quad \overline{AE} = \overline{AB} = 16 \) .
\( \overline{HE} = \frac{1}{2} \overline{AE} = \frac{1}{2} 16 = 8 \)
Hence
\( A = \frac{1}{2} (24 + 16) \times 8 = 160 \)
The area of the arrow is twice the area of the trapezoid. Hence
The area of the arrow is equal to \( 2 \times 160 = 320 \; unit^2\)
We decompose the given shape into basic shapes whose areas are easily calculated using formulas.

Area of isosceles triangle ABG \( = \frac{1}{2} \times 4 \times 4 = 8 \)
Area of trapezoid BCFG \( = \frac{1}{2} \times 2 \times (4+1) = 5 \)
Area of trapezoid CDEF \( = \frac{1}{2} \times 3 \times (1+3) = 6 \)
Area of semicircle of diameter DE \( = \frac{1}{2} \times \pi \times 1.5^2 = 3.14 \times 1.5^2 = 3.53 \)
Total area of the shaded region \( = 8 + 5 + 6 + 3.53 = 22.53 \; mm^2 \) , rounded to two decimal places.
18 - Volumes and Surface Area

The volume of half the sphere \( = \frac{1}{2} \times \frac{4}{3} \pi r^3 = \frac{4}{6} \times 3.14 \times 6^3 = 452.16 \; m^3\)
The volume of the cylinder \( = \pi \times r^2 \times h = 3.14 \times 6^2 \times 10 = 1130.4 \; m^3 \)
The surface area of half the sphere \( = \frac{1}{2} \times 4 \times \pi \times r^2 = 2 \times 3.14 \times 6^2 = 226.08 \; m^2\)
The surface area of the cylinder (without the bottom) \( = 2 \times \pi \times r \times h = 2 \times 3.14 \times 6 \times 10 = 377.00 \; m^2\)
Total volume of silo \( = 452.16 + 1130.4 = 1582.56 \; m^3 \)
Total surface area of silo \( = 226.08 + 377.00 = 603.08 \; m^2 \)
Because of the symmetry of the rectangular prism, the volume of the triangular prism is equal to half the volume of the rectangular prism

Volume of the given rectangular prism \( = 6 \times 3 \times 4 = 72 \; unit^3\)
Volume of the triangular prism \( \frac{1}{2} \times 72 = 36 \; unit^3\)
The surface area of the triangular prism is equal to half the surface area of the rectangular prism to which we add the area of the rectangle ABCE made by the red diagonals and the edges AE and BC of the rectangular prism.
Surface area of the rectangular prism \( = 2 \times ( 6 \times 3 + 3 \times 4 + 6 \times 4 ) = 108 \; unit^2\)
Use the Pythagorean theorem to find the length \( d \) of the diagonal which is the hypotenuse (red) of the right triangle CDE.
\( d^2 = 3^2+4^2 = 25 \)
Use square root to find
\( d = 5 \)
Area of the rectangle made by the diagonals and the edges \( = 5 \times 6 = 30 \; unit^2\)
Surface area of the triangular prism \( = \frac{1}{2} \times 108 + 30 = 84 \; unit^2\)
Note that there are other ways to find the volume and surface area of the rectangular prism.
19 - Data and Graphs
a)
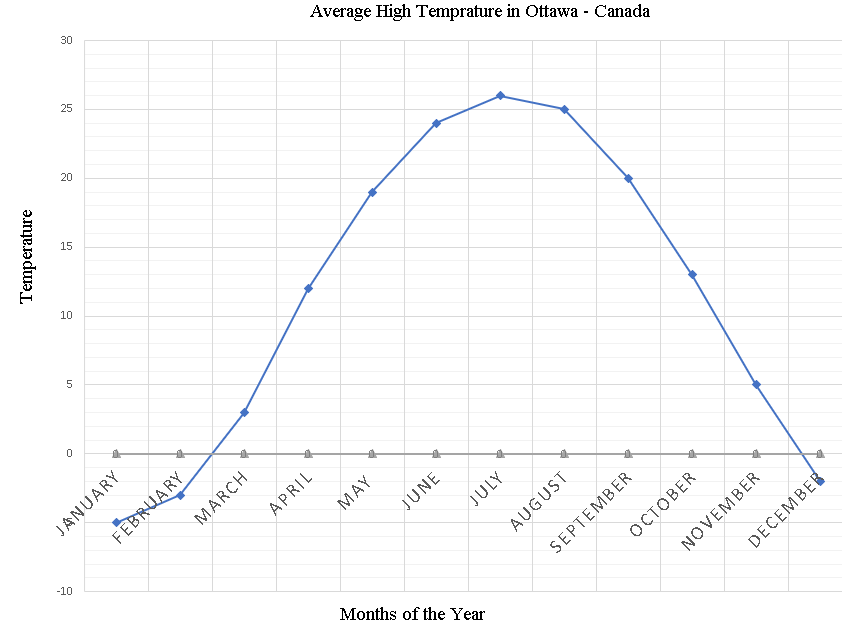
January has the lowest average temperature of \( -5^{\circ} \) and is therefore the coldest month.
b)
July has the highest average temperature of \( 26^{\circ} \) and is therefore the hottest month of the year.
c)
Difference in temperature between the coldest and hottest months \( = 26 - (-5) = 31^{\circ} \)
d)
The smallest increases is from January to February and from June to July
e)
The smallest decrease is from July to August
a) The given data in order from smallest to the largest values is as follows
\( 31, 44, 45, 54, 55, 56, 60, 64, 67, 67, 69, 70, 76, 76, 77, 78, 79, 84, 85, 86, 88, 89, 91, 92, 97 \)
b)
Range = Largest value - smallest value \( = 97 - 31 = 66 \)
c)
Start with the class \( 30 - 39 \) and add the class width to obtain the remaining classes and cover all data values with a maximum value of \( 97 \).
To obtain the next class, we add \( 10 \) to the lower and upper limits of a given class.
Hence the next class after the class \( 30 - 39 \) is given by
\( (30 + 10) - (39 + 10) \) = \( 40 - 49 \)
and continue until all data values are covered as shown in the frequency table below

d)
A histogram is made using the number of student in the vertical axis and the classes on the horizontal axis as shown below.

e)
The scores in the three classes \( 3-39 \) , \( 40-49 \) and \( 50-59 \) are below 60 and the number of students in these classes may be found in the frequency table and the histogram.
1 students in the class \( 3-39 \)
2 students in the class \( 40-49 \)
3 students in the class \( 50-59 \)
The total number of students who failed is equal to
\( 1 + 2 + 3 = 6 \)
The percentage of students who failed is given by
\( \frac{\text{Number of Students who failed} }{\text{Total Number of Students}} = \frac{6}{25} = 0.24 = 24\% \)
20 - Statistics
First order the data values from the smallest to the largest.
\( \{ 0 , 1 , 2 , 2 , 3 , \color{red}{3} , 3 , 4 , 9 , 9 , 10\} \)
The median is the value in the middle (red) which is \( 3 \)
The lower quartile is the median of the data values below the median \( 3 \) which in the above data is \( \{0 , 1 , \color{red}2 , 2 , 3 \} \)
lower quartile = \( 2 \)
The upper quartile is the median of the data values above the median \( 3 \) which in the above data is \( \{ 3 , 4 , \color{red} 9 , 9 , 10 \} \)
upper quartile = \( 9\)
Let \( x \) be the score of the fifth quiz. The average of the 5 quizzes is given by
\( \frac{83 + 94 + 97 + 93 + x}{5} \)
The average "is at least 90" is mathematically written as
\( \frac{83 + 94 + 97 + 93 + x}{5} \ge 90 \)
Multiply both sides of the above inequality by 5
\( \frac{83 + 94 + 97 + 93 + x}{5} \times 5 \ge 90 \times 5\)
Simplify
\( 83 + 94 + 97 + 93 + x \ge 450 \)
Solve for \( x \)
\( x \ge 450 - (83 + 94 + 97 + 93) \)
\( x \ge 83 \)
Mark needs to score at least \( 83 \) in the fifth quiz in order to have an average which is at least \( 90 \)
21 - Probabilities
Sample space = all possible outcomes = \( \{ 1,2,3,4,5,6 \} \)
Set of even numbers among the outcomes = \( \{ 2,4,6 \} \)
There are \( 6 \) possible outcomes from which \( 3 \) are even; hence
probability of getting an even number \( = \frac{\text{Number of elements in the set of even numbers}}{\text{Number of elements in the sample space}} = \frac{3}{6} = \frac{1}{2} \)
a)
Probability of getting a tail is \( \quad P_1 = \frac{1}{2} \)
Probability of getting a "4" is \( \quad P_2 = \frac{1}{6} \)
The events are independent and therefore
The probability of getting a tail (coin) and a 4 (die) = \( \quad P_1 \times P_2 = \frac{1}{2} \times \frac{1}{6} = \frac{1}{12} \)
b)
Probability of getting a head is \( \quad P_3 = \frac{1}{2} \)
Probability of getting an odd number is \( \quad P_4 = \frac{3}{6} = \frac{1}{2} \)
The events are independent and therefore
The probability of getting head (coin) and an odd number (die) \( \quad P_3 \times P_3 = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} \)
a)
Using the counting principle, we have \( 3 \times 3 = 9 \) possible outcomes written as: \[ (1,1) , (1,2), (1,3) , (2,1) , (2,2), (2,3) , (3,1) , (3,2), (3,3) \] There is one outcome with \( 3 \) in both random selections and that is \( (3,3) \)
Hence
The probability of selecting 3 in both random selections \( = \frac{1}{9} \)
b)
Three of the \( 9 \) possible outcomes have the same number in both random selections and these are: \( (1,1) \) , \( (2,2) \) and \( (3,3) \)
The probability of selecting the same number in both random selections \( = \frac{3}{9} = \frac{1}{3} \)
If 5 said blue was their favorite color and 6 said brown was their favorite number, then
\( 20 - 5 - 6 = 11 \) picked a color that is neither blue nor brown
Hence the probability that the next student surveyed will pick a color that is neither blue nor brown is given by
\( \frac{11}{20} \)