Problemas y Preguntas sobre Triángulos para Grado 8 con Respuestas

Se presentan problemas y preguntas con respuestas sobre triángulos para 8º grado. Estos ejercicios abarcan cálculos de ángulos, perímetros y áreas de triángulos. Se incluyen preguntas sobre triángulos semejantes. También se proporcionan soluciones y explicaciones detalladas.

  1. Las longitudes de dos lados de un triángulo son 20 mm y 13 mm. ¿Cuál de estas longitudes no puede representar la longitud del tercer lado?
    1. 35 mm
    2. 10 cm
    3. 20 mm
    4. 45 mm
  2. ABC es un triángulo isósceles. Calcula la medida del ángulo ABC.
    triángulo isósceles problema 1
  3. El perímetro de un triángulo equilátero es de 210 cm. ¿Cuál es la longitud de un lado de este triángulo?
  4. Encuentra el valor de x para que el triángulo mostrado sea un triángulo rectángulo.
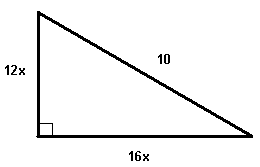
    triángulo rectángulo problema 3
  5. ¿Cuáles serán los vértices del triángulo obtenido al reflejar sobre el eje a el triángulo definido por los vértices (1,2), (2,-3) y (4,-1)?
  6. Los dos triángulos mostrados son semejantes. Halla la longitud de la hipotenusa del triángulo mayor.
    triángulos semejantes problema 5
  7. Una escalera de 13 pies está apoyada contra una pared vertical. El punto más bajo de la escalera está a 4 pies de la pared. ¿Cuál es la altura del punto donde la escalera toca la pared? (redondea a la décima más cercana).
  8. La longitud de la hipotenusa de un triángulo rectángulo es 40 cm. La medida de uno de sus ángulos es 45 grados. ¿Cuáles son las longitudes exactas de los otros dos lados?
  9. El triángulo ABC es isósceles. La longitud de la base es 20 metros y la altura correspondiente es 24 metros. Calcula el perímetro de ABC (redondea a la décima más cercana).
  10. Un triángulo tiene un área de 90 cm². Halla la longitud de la base si esta mide 3 cm más que la altura.
  11. El perímetro de un triángulo es 74 pulgadas. La longitud del primer lado es el doble del segundo lado. El tercer lado es 4 pulgadas mayor que el primero. Encuentra la longitud de cada lado.
  12. Determina el área del triángulo delimitado por las rectas y = -4, x = 1 y y = -2x + 8.
  13. Demuestra que el triángulo con vértices A(-1,6), B(2,6), C(2,2) es rectángulo y calcula su área.

Respuestas a las Preguntas Anteriores

  1. 35 mm, 10 cm = 100 mm y 45 mm no pueden ser el tercer lado.
  2. 54 grados
  3. 70 cm
  4. 1/2
  5. (1,-2), (2,3) y (4,1)
  6. La hipotenusa mide 25 unidades
  7. 12.4 pies
  8. 20√2 cm
  9. 72 metros
  10. 15 cm
  11. 28, 14, 32
  12. 25 unidades cuadradas
  13. Calcula las distancias: d(A,B)=3, d(B,C)=4 y d(A,C)=5. Como d(A,B)² + d(B,C)² = d(A,C)², por el recíproco del teorema de Pitágoras, el triángulo es rectángulo.

Más Referencias y Enlaces